[기계학습] Logistic Regression - Systemic Formulation

Recap) Regression

Machine learning에서 regression task는 conditional expecatation $\mathbb{E}[y|x]$를 찾는 것이다. 이는 $d$차원의 input과 $d'$ 차원의 output을 mapping하는 function을 찾고자하는 것과 같다. 그러나 때때로 output을 $[0, 1, 2, 3]$과 같이 discrete support로 한정하고 싶을 때가 있다. Computer vision 분야에서는 object를 detection을 해서 어떠한 물체인지 판단하는 task를 주로 다루곤 한다. 이러한 메커니즘을 만들기 위해서는 classification algorithm이 필요하다. 이때 classification은 regression과는 다소 차이점이 존재한다. Regression은 real number를 예측하는 반면에 classification task에서 원하는 것은 output이 discrete number 혹은 class로 예측하고자 한다. Object detection에서는 각각 어떠한 물체인지 classification task를 한다고 볼 수 있다.

Classification

Classification의 목적은 input feature vector $x$를 $K$개의 discrete class $C_k$ 중 하나로 할당하고자 하는 것이다. 예를 들어 spam filtering의 경우 binary classification으로 해당 메일이 스팸 메일인지 아닌지를 구분하게 된다.

Decision Boundary

예를 들어 2개의 class $C_1, C_2$가 있다고 해보자. Binary로 정한 이유는 가장 대표적인 예시이기 때문이다. 즉, 이번에 binary classification에 대해서 알아보려고 한다. 현실에서는 선택을 해야하는 경우가 굉장히 많으며 대부분 2가지 선택지를 마주하게 된다. 2개의 class 중에서 만약 $C_1$이 아니라는 이야기는 자연스럽게 $C_2$에 해당하게 됨을 알 수 있다.

2개의 class를 구분하는 classifier가 있다고 했을 때 decision region $\mathcal{R}_1$에 새로운 data point $x$가 존재한다면 이를 $C_1$에 할당하고자 한다. 여기서 decision region이라는 것은 data point에 class를 할당하기 위한 영역이라고 생각하면 되고 이 영역 안에 해당 data가 존재한다면 해당 class라고 판단한다는 것이다. 그리고 이러한 영역을 나눠주는 경계 부분을 decision boundary 혹은 surface라고 한다.

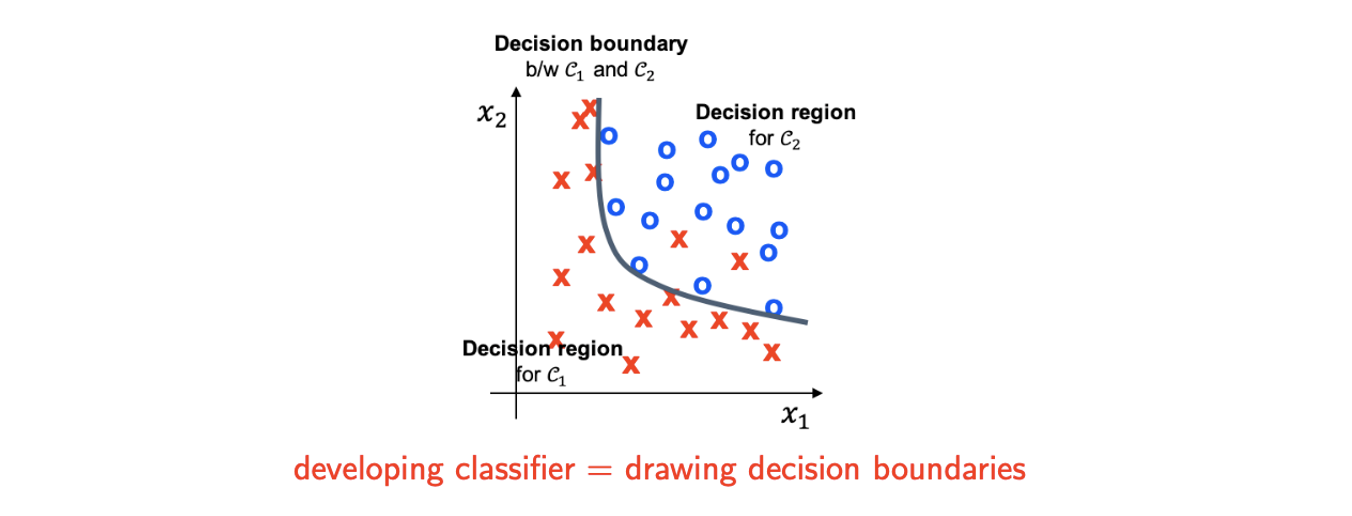위와 같은 binary classification의 경우 decision boundary를 경계로 양쪽이 서로 다른 class를 할당하게 된다. Classification task는 결국 data에 class lable을 decision boundary를 기준으로 할당하게 되는 것이고, 결국 이러한 decision boundary를 그린다는 것이 결국 classifier를 만드는 것과 같은 것이다.

Linear Regression for Classification?

Linear regression을 classification으로 확장할 수 있다고 생각하는 것은 일리가 있다. 먼저 dataset $\mathcal{D}=(x_n,y_n)_{n\in[N]}$이 있고 각각의 data point $(x_n,y_n)$에서 $x_n\in\mathbb{R}$이고 $y_n=\{-1,+1\}$이라고 가정할 것이다. $[N]$이라는 notation은 1부터 $N$까지의 양수들의 집합 $\{1,\dots,N\}$이라고 생각하면 된다. $y_n$은 2개의 값을 가지고 있어서 $x_n$에 2가지 선택지 중 하나를 부여하는 상황이라 결국 이를 binary classifiaction task로 볼 수가 있는 것이다.

그리고 linear model $y=w_1x+w_2$라고 가정하게 되면, classifier $h$는 다음과 같이 정의할 수 있다. 결국 classification이라는 것이 linear regression의 output $y$를 하나의 값으로 mapping하고자 하는 것이기에 범위만 정해주게 되면 2가지 선택지를 각각 할당할 수 있게 된다.

결국 linear model이 음수를 가지게 되면 -1을, 양수를 가지게 되면 +1을 할당하게 되는 것이다. 우리는 $w=(w_1,w_2)$를 찾기 위해서 다음과 같은 loss function을 학습을 할 것이고, 이는 다음과 같이 squared error를 작게 만들고자 하면 된다. 결국 error를 최소한으로 만들고자 하는 것으로 실제 $y_n$값 +1, -1과 linear model이 할당받은 +1, -1이 같게 되면 0가 되어 loss에는 영향을 주지 않을 것이다. 반면 +1인 data point를 -1이라고 한다면 이는 loss에 영향을 주어 결과적으로 error가 커지게 될 것이다. 우리는 이러한 error를 최대한 줄이고자 하는게 목적이기에 다음과 같이 loss를 만들 수 있고 이때 이 값을 최소로 만드는 $w$를 찾으면 되는 것이다.

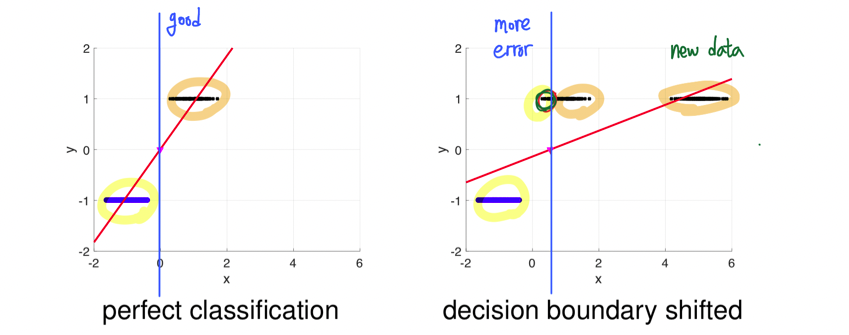좌측과 같은 data point가 존재할 때 파란점들은 -1을 할당하게 되고 검은점들은 +1을 할당하게 될 것이다. 이러한 경우 linear model을 사용해서 least square formulation을 통해서 classifier로서 빨간선을 얻게 된 것이다. 빨간선은 $x=0$에서 decision boundary를 형성한다고 했을 때 error가 전혀 없는 완벽한 경우이다.

우측은 기존의 data에다가 새로운 data를 추가하게 되면 빨간선이 새롭게 형성이 되고, 즉 새로운 classifier가 만들어지게 된다. 이때 decision boundary의 경우 $x=0$에서 조금 이동하게 되고 이는 기존에는 완벽하게 분류했던 결과에 대해서 error를 만들어내게 된다.

이러한 점에서 data가 간단하게 분포하고 있더라도 linear regression을 통해서 완벽하게 binary classification을 수행하는데 어려움이 존재한다. 물론 decision boundary를 상황에 맞춰 변경한다면 정확하게 분류할 수 있다고 생각할 수 있지만, 이미 decision boundary를 0으로 두고 진행을 했다는 것 자체에서 더이상 decision boundary에는 신경을 쓰지 않겠다는 이야기와 같다. 그래서 이러한 문제를 해결하고자 classification에 대해서 linear regression을 사용하지 않고 새로운 방안으로 logistic regression을 사용할 것이다.

A Systemic Formulation: Logistic Regression

Classification task에 대해서는 linear regression은 적합하지 않다. 그래서 classification에서 대안으로 사용되는 logistic regression에 대해서 이제부터 알아보고자 한다.

Discriminant Function

Classifier를 대신해서 설명할 수 있는 discriminant function에 대해서 먼저 알아볼 것이다. Discriminant function은 기존의 classifier을 대체하는 표현이며 특정 class $k$에 속하는 data point의 점수를 세는 function들의 집합이다. Discriminant function은 $\{f_k\}_{k=1,\dots,K}$로 ${f_1, \dots, f_k}$ 다음의 classification rule을 만족하게 된다.

만약 $k$의 score 혹은 discriminant function이 가장 큰 값을 가진다면, 우리는 data point $x$에 class $k$를 할당해서 classification을 할 것이다. Discriminant function을 선택하는 자연스러운 방법 중 하나는 다음과 같다.

그러면 classifier는 다음과 같이 간단하게 나타낼 수 있다.

즉, score를 최대로 만드는 class $k$를 찾겠다는 이야기다. 그러면 linear regression의 경우 linear discriminant function $f_1(x)=ax+b, f_2(x)=0$과 같이 생각해볼 수 있다. Classification task를 discriminant function의 관점에서의 linear regression으로 생각할 수 있다는 것이다.

Bayes Decision Rule

우리는 이제 discriminant function이 여러개가 존재한다고 했을 때 optimal discriminant를 찾고자하는 것이 목표이다. 유명방 방법 중 하나로 Bayes decision rule을 사용하면 다음과 같이 discriminant function을 선택할 수 있다.

우리는 $f_k$를 계속 비교해야 할 것이고 이때 동일한 classification을 표현하기 위해서 discriminant function에 상수인 양수를 곱해도 전혀 상관이 없다. 그래서 posterior은 다음과 같이 다시 표현할 수 있기 때문에 이러한 Bayes rule은 위와 같이 적을 수가 있는 것이다.

Normalization factor는 $x$에 대한 constant이다. 그래서 이는 상관이 없어서 무시하게 되면 분자만 남게되어 위와 같은 형태가 된다. 분자의 경우 2개로 나뉘는데 하나는 class prior이고 다른 하나는 class-conditional density이다. 이는 model을 빌드하는데 더 자연스러운 방법이다. 왜냐하면 예를 들어 사람의 특징을 분류하고 확인하고자 한다면 generative model을 생각하는 것이 더 자연스럽기 때문이다. 그리고 이러한 Bayes rule에 의한 식은 수학적으로 tractable하기에 계산하는데 어려움이 없어지게 된다. 그러면 이제 Bayes decision rule의 optimality에 대해서 알아볼 것이다.

Optimality of Bayes Decision Rule

우리가 최대로 만들고 싶은 것은 accuracy로 각 data point를 완벽하게 분류하고 싶은 것이다. 이는 첫번째 등호에서 decision region $\mathcal{R}_k$로 설명할 수 있는 classifier들의 합으로 나타낼 수 있다. 그러면 이제 이 확률은 두번째 등호에서 conditional probability의 정의에 따라 다시 적을 수 있다. 그러면 다시 세번째 등호에서 class $k$가 주어졌을 때 observation $x$의 확률에 대한 integration 형태로 다시 적을 수가 있다. Correct의 확률을 보면 결국에 우리는 Bayes decision rule이 optimal하다는 것을 쉽게 확인할 수 있다. 왜냐하면 Bayes decision rule은 항상 decision region을 설정해서 확률을 최대로 만들려고 노력하기 때문이다. 이를 이번에는 graphical illustration으로 optimality를 확인할 수도 있다.
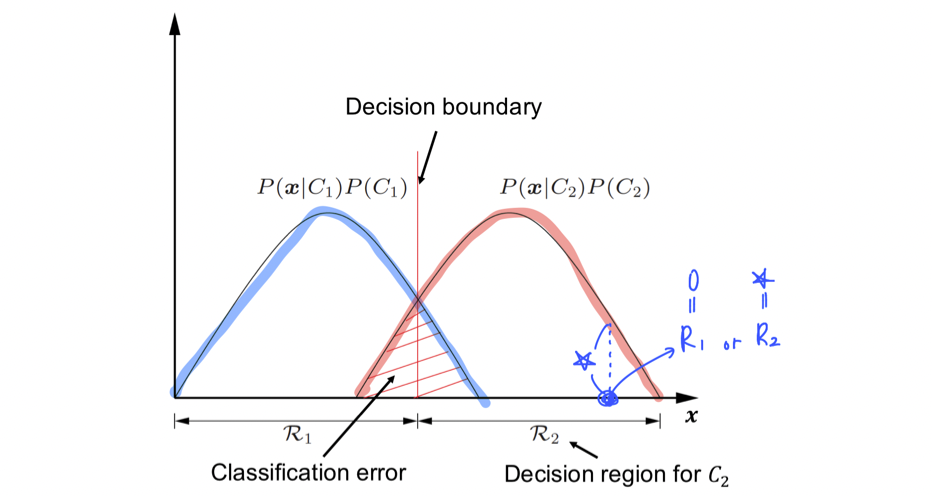Classification은 아주 작은 region이 $\mathcal{R}_1$과 $\mathcal{R}_2$ 중 어디에 속하는지를 결정하는 작업이다. 위에서 마지막 등호에 있는 확률의 적분값의 합을 최대로 만들고자 한다. 그래프에서 파란 그래프는 $p(x|C_1)p(C_1)$로 빨간 그래프는 $p(x|C_2)p(C_2)$라고 했을 때, 만약 위와 같이 파란점을 $\mathcal{R}_1$이라고 하면 해당 지점에서의 확률을 모두 잃어버리게 되어 적분 값의 합을 최대로 만들 수가 없다. 그래서 파란점의 경우 $\mathcal{R}_2$라고 해야 온전히 그 값을 다 가져갈 수 있어 우리의 목적에 부합하게 된다. 만약 교차하는 지점에 있는 data point에 대해서는 해당 지점에서의 확률이 더 큰 쪽을 선택하면 되는 것이다.

Logistic Regression and Probablistic Model

지금까지는 우리가 accuracy는 최대로 만들고 error를 최소로 만드는 Bayes decision rule에 대해서 살펴보았다. Logistic regression은 Bayes decision rule의 관점으로부터 다음과 같이 classification을 위한 확률적인 접근을 수식으로 할 수가 있게 되었다.

이를 간단하게 다음과 같이 한번에 나타낼 수도 있다.

Logistic regression은 이렇게 discriminant function으로 나타낼 수 있고, 만약 여기서 feature extractor $\phi$가 있다면 $x_n$ 대신에 $\phi(x_n)$을 적을 수도 있다.

Linear vs. Logistic

Linear regression은 다음을 만족시키려고 했다.

그러나 분명한 것은 이렇게 하면 linear function의 특성상 unbounded function이 되어 $x$가 증가함에 따라 한쪽 방향의 무한대로 수렴할 수 있게 된다. 이는 적절한 형태의 식이 아니다. 반면, logistic regression의 경우 다음과 같은 sigmoid function을 사용하게 되어 0과 1사이의 범위로 값을 가질 수 있게 된다.

이렇게 식을 나타내면 확률에 근사하는데 더욱 적절한 형태가 된다. 그래프 상에서 lienar model과 logistic model을 나타내면 다음과 같다.

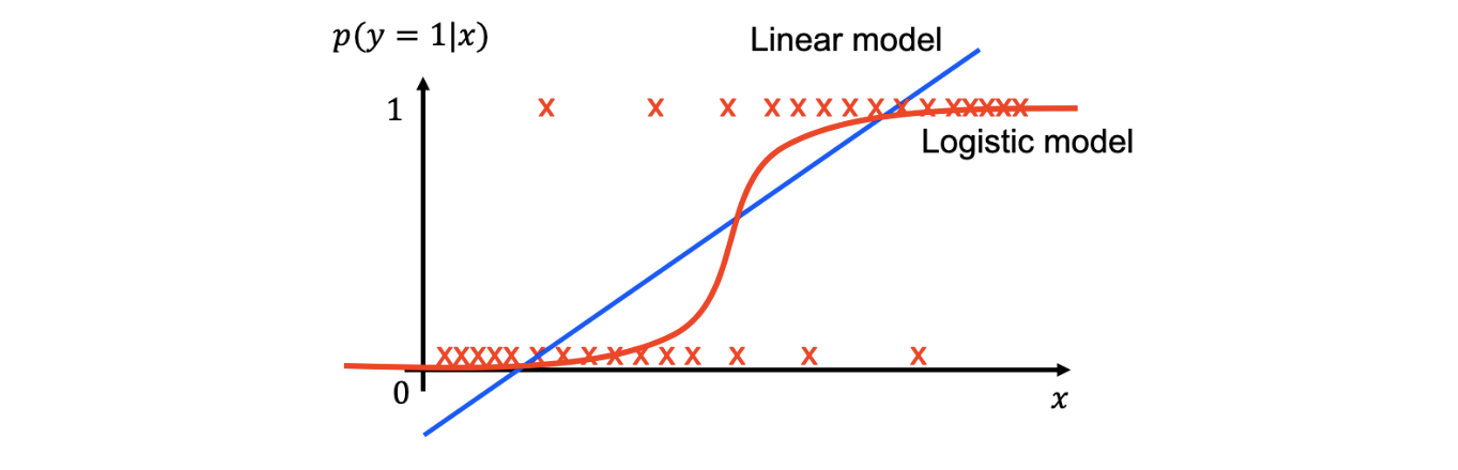본질적으로 linear model과 logistic model 모두 regression task를 위한 regressor이다. 그래서 이들이 하고싶은 것은 input $x$와 $p(y=1|x)$라는 확률을 연결시키고 싶은 것이다. 위와 같이 빨간 엑스들이 data point라고 했을 때 linear model은 파란선과 같이 binary classification을 진행하고자 하고 logistic model은 빨간선과 같이 binary classifcation을 수행하고자 한다. 보다시피 logistic model이 위와 같이 분포된 dataset에 더 그럴듯해 보이는 것을 확인할 수 있다.

우리는 0.5라는 확률을 기준으로 binary classification을 한다고 했을 때, 두 model 모두 동일한 decision boundary를 형성하게 될 것이다. 그러나 linear modeld의 경우 model과 data 사이의 거리의 차이가 꽤 큰 부분도 존재해서 error가 크게 나타나게 될 것이다. 그래서 위와 같이 간단한 분포에 대해서는 logistic model을 사용하는 것이 error를 줄이는데 적합할 것이다. 그래서 classfication에 대해서 logistic model이 더 적절하게 사용될 수 있다.

Property of Logistic Function

다음은 logistic function에 대한 몇가지 성질들을 보여주고 있다. 이 중에서 가장 마지막에 있는 성질은 정말로 자주 사용되는 성질이니까 확인해두면 좋을 것이다.

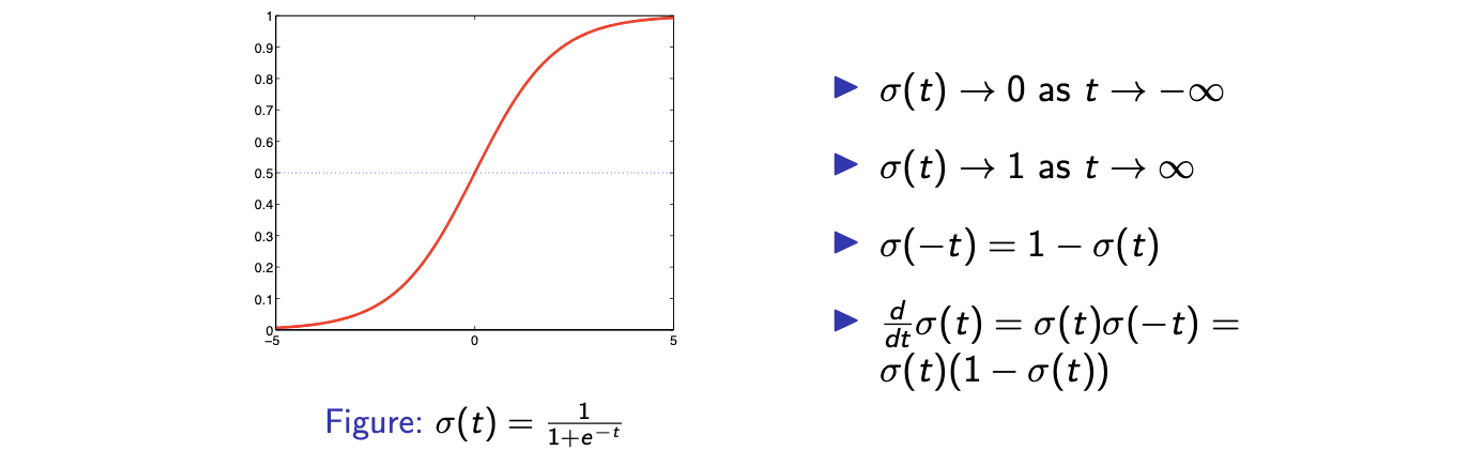
Optimization for Logistic Regression

Classifier를 학습시키기 위해서는 learning algorithm을 만들 필요가 있고, 이를 위해서 MLE를 사용하여 Bayes decision rule을 학습하고자 하는 것이 자연스럽다. 우리가 최대로 만들고 싶은 것은 model이 주어졌을 때 data point에 대한 likelihood이고, 여기서 각 data point가 i.i.d.를 만족한다는 가정이 있어서 likelihood 대신에 log-likelihood를 다음과 같이 각각의 log-likelihood의 summation으로 나타낼 수 있다.

Logistic regression에서의 probablistic model는 다음과 같다.

따라서 logistic regression은 다음과 같은 loss function을 최소로 만들고자 한다. 사실 우리는 위와 같은 확률을 최대로 만들고 싶은 것이지만 분자와 분모를 바꾸는 음의 부호를 통해서 다음과 같이 minimization problem으로 바꿀 수가 있다.