[기계학습] Multi-Class Classification and Kernel Method

JAEYOON SIM·2021년 10월 22일

Machine Learning

목록 보기

17/35

Binary classification은 보통 yes / no로 대답할 수 있는 task에 대해서 이루어진다. 가령, image classification에서 이미지가 고양이인가 아닌가에 대해서 분류하기도 하고, edge detection에서 주어진 픽셀이 경계선에 위치했는가에 대해서 분류하기도 하며, object detection에서 이미지에 고양이가 존재하는가에 대해서 분류할 수도 있다. 현실에는 이렇게 2가지 경우에 해당되는 task도 있지만 3개 이상의 multi class를 분류해야하는 task도 존재한다. 그리고 우리는 이를 multi-class classification이라 부르는 것이다. 이미지를 주고 이미지에 있는 동물이 많은 동물들 중에서 어느 동물인지 분류할 수도 있다.

Discriminant Function

우리는 classifier를 discriminant function 혹은 discriminant score $f_k$ 로 설명할 수 있다. $f_k$ 는 주어진 $x$ 에 대해서 어느 class에 속하는지에 대한 score를 측정하거나 likelihood를 계산할 수 있다. 그래서 classifier $h(x) = \operatorname*{arg\,max}_k f_k(x)$ 로 정의하고, $h(x)$ 는 score를 최대화하려고 할 것이다. 이러한 discriminant function을 고르는 쉬운 방법 중 하나는 likelihood를 사용하여 $f_k(x) = p(C_k | x)$ 로 고르는 것이다.

Multi-class Logistic Regression for Classification

그리고 logistic regression에서 model은 데이터 $x$ 에 대하여 lable $y$ 에 대한 확률로 다음과 같이 정의할 수 있다.

p(y=k|x) = \frac{exp(w_{(k)}^T \phi(x))}{\sum_{j=1}^K exp(w_{(j)}^T \phi(x))}

이 model을 사용하게 되면 classifier는 $k$ 를 최대화 하는 $w_{(k)}^T \phi(x)$ 찾아야 한다. $w$ 를 배우기 위해서 maximum likelihood estimation를 다음과 같이 formulate 할 수 있고, 이는 negative log likelihood를 최소화하는 $w$ 를 찾도록 바꿀 수가 있다.

\operatorname*{arg\,max}_w \prod_{\substack{i=1,...,N}} p(y=y_i|x^{(i)})=\operatorname*{arg\,min}_w - log p(y=y_i|x^{(i)})

그러면 이렇게 해서 multi-class logistic regression을 설명하게 된다. 그래서 $w$ 혹은 각각의 class가 주어졌을 때, 다음과 같이 특정 class를 계산할 수 있는 선을 그릴 수 있다.
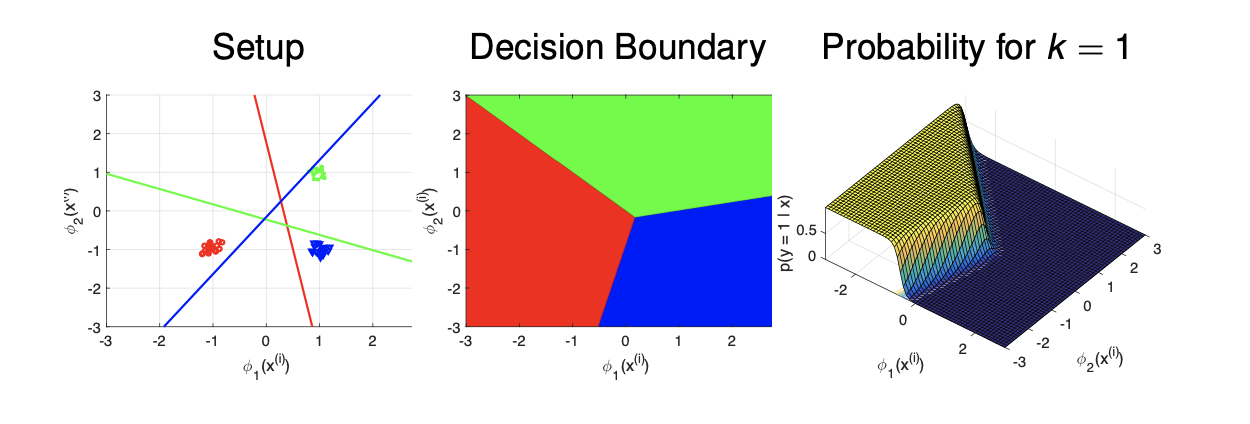그러면 decision boundary는 위와 같이 결정이 된다. 만약 $K$ 가 2라면 다음과 같다.
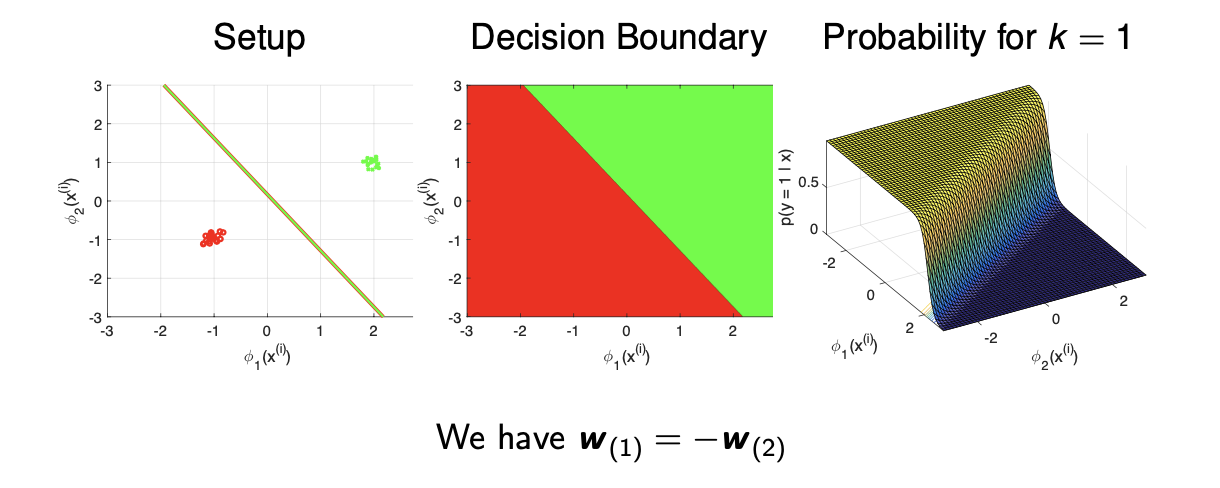특히 우리가 $K$ 가 2라는 것은 binary logistic regression에 대해서 집중하여 결정하고 싶은 것이고 이는 multi-class logistic regression이 binary logistic regression로 일반화 되는 것이다. 이러한 경우에는 각각의 class에 대해서 $w$ 는 서로의 negative가 된다. 지금까지가 어떻게 logistic regression을 multi-class에 대해서 generalize하는가였고, 이제부터 multi-class SVM에 대해서 알아보려고 한다.

Binary SVM: Drawing Hyperplane

지금부터 multi-class SVM에 대해서 집중적으로 알아보고자 한다. 시작하기 전에 2개의 class를 나누는 hyper plane을 train하는 binary SVM에 대해서 간단하게 보려고 한다.
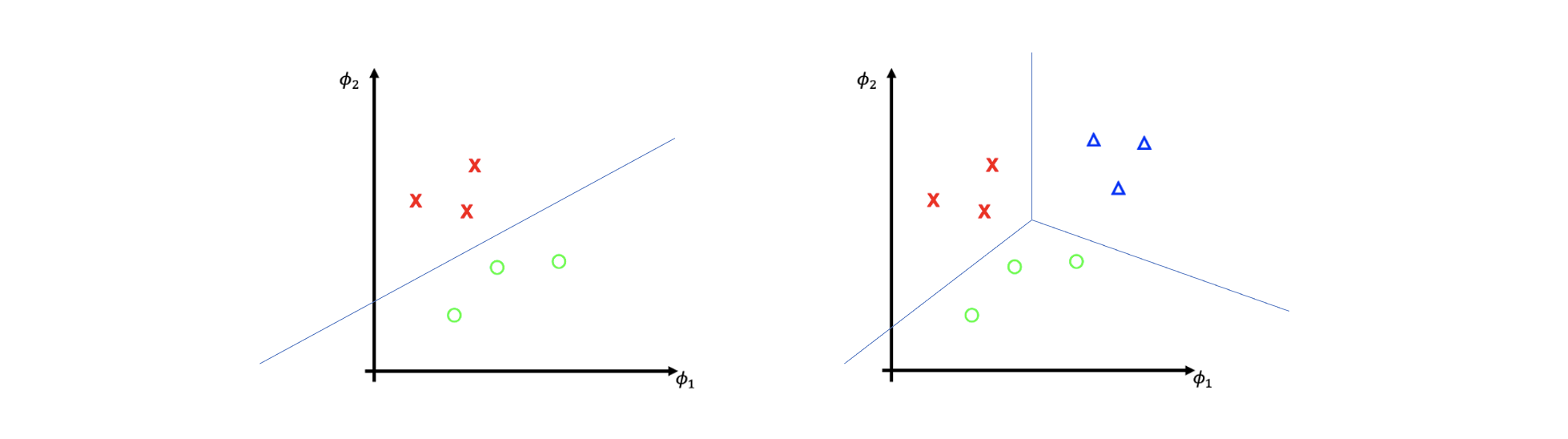좌측과 같이 2개의 class 데이터가 있을 때, 가운데 선을 그려서 이 둘을 나누고 싶다. 이는 SVM이 이러한 hyper plane을 그리도록 하는 것이다. 만약 class가 3개가 되면 어떻게 될까? 간단하게 생각해서 binary SVM에서와 같이 데이터를 나누는 hyper plane을 조합해서 여러 class의 데이터를 나누고 싶다. 위의 선은 임의로 그려본 것이다. 이러한 선들을 여러개 그려 데이터를 나누는 방식은 몇가지가 존재한다.

Approach 1: One vs. Rest (OvR)

첫번째는 하나와 나머지를 나누는 것이다. 이름은 One-vs-Rest (OvR), One-vs-All (OvA), One-against-All (OAA) 등과 같이 부르면 된다. 여기서 하고 싶은 것은 binary SVM을 multi-class에 대해서 하고 싶은 것이다. 즉, 1개의 class를 대상으로 나머지 전부를 나누는 K개의 binary SVM을 하려고 한다.
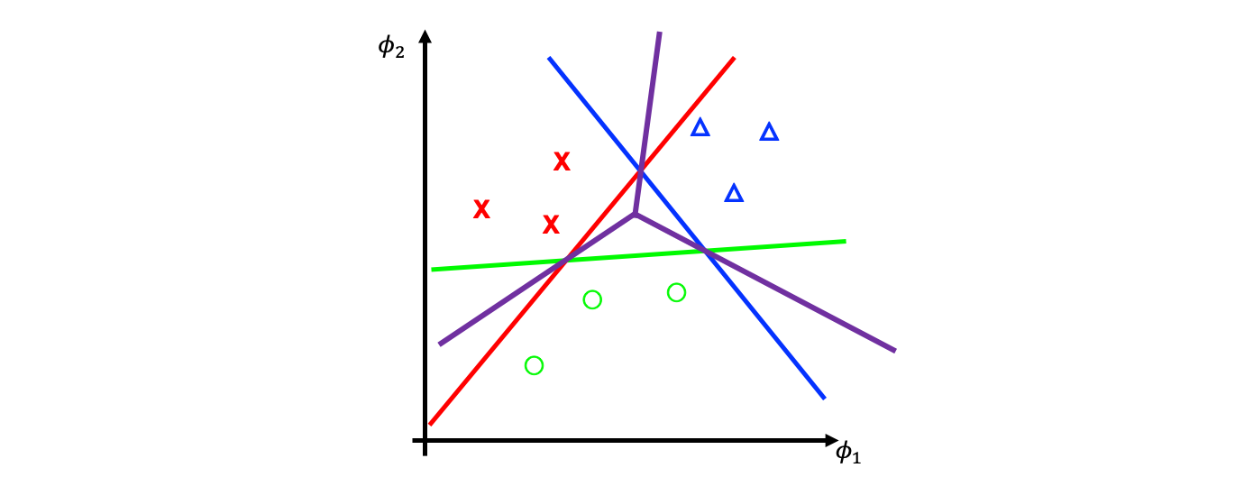각각의 class에 대해서 자신을 제외한 나머지 class들을 나누는 hyper plane을 그릴 수 있다. 그러면 위와 같이 red, blue, green 선을 각각 그리게 되고, 이들을 조합하여 decision boundary를 나타내는 purple 선을 그리고자 한다. 이 방식은 그럴듯해 보이지만 risk가 존재한다. 만약 green 데이터의 개수가 red, blue 데이터에 비해 엄청나게 적게 존재한다면, $w_{green}$ 은 green이냐 아니냐로 분류하려고 할 것이고 bias가 생길 것이다. 이러한 imbalance 문제는 적은 양의 class에 대해서 제대로 classification을 하지 못한다.

Approach 2: One vs. (another) One (OvO)

이러한 imbalacne 문제를 피하기 위해서 하나의 class와 다른 하나의 class를 나누는 방식에 대해서 생각해 볼 수 있다. 이는 K개의 class 중에서 2개를 골라야 하기 때문에 $\frac{K(K-1)}{2}$ SVM이 된다. 그리고 각각의 SVM은 $(w_{jk}, b_{jk})$ binary classification으로 나타낼 수 있고, 이들은 class $k$ 와 $j$ 를 나누려고 할 것이다.
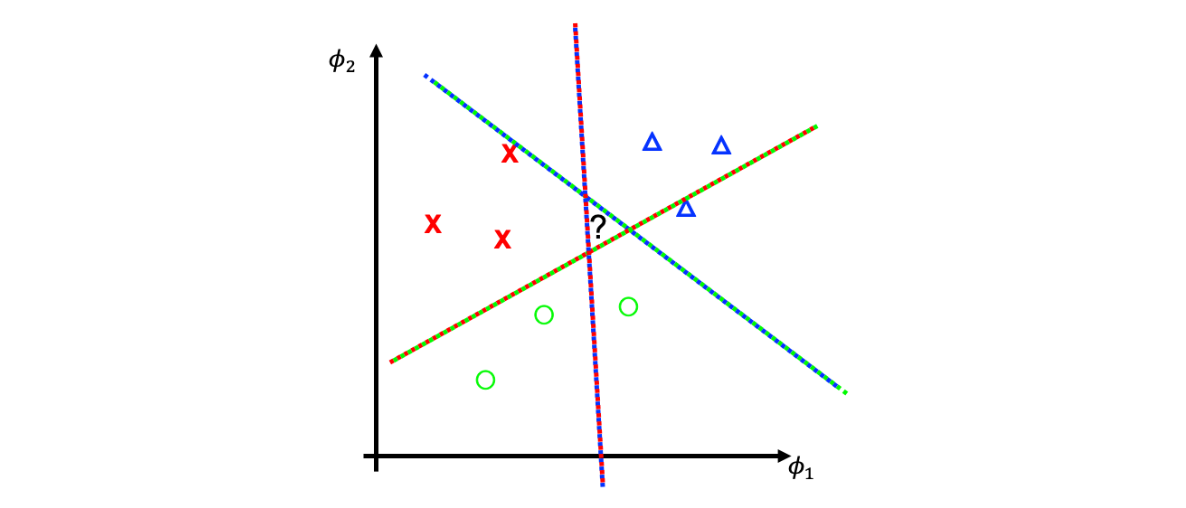여기서는 단순히 자신과 다른 하나의 class를 나누기만 한다. 이렇게 하면 class imabalance 문제는 발생하지 않게 된다. 그러나, 위에서 중간에 ? 공간이 생기게 되고 이것이 문제가 된다. 우리는 이 공간에 대해서는 똑똑하게 break-tie 해야한다. 만약 새로운 데이터가 등장하게 되고 이 공간에 존재하게 된다면 우리는 어떻게 이 데이터를 어떤 class라고 당당하게 이야기할 수 있을까? 우리는 모든 SVM에 대해서 majority vote를 통해서 결정하면 된다. 만약에 red, blue 사이에 data가 등장했다고 생각해보자. 그러면 각각의 $w$ 에 대해서 일종의 투표를 해주는 것이다. 위의 예시는 3개의 hyper plane이 존재하고, 그래서 어느 쪽에 더 가까운지 투표를 해서 (red, red, blue)가 나오게 되면 이 데이터는 red에 속하도록 결정되는 것이다. 그런데 만약 이렇게 등장한 데이터가 ? 영역에 속하게 되면 majority vote 방식이 의미가 없어진다. 각각의 경우에 대해서 하나씩 나와 동률이 되어 어느 class인지 나눌 수 없기 때문이다.

OvR and OvO SVM

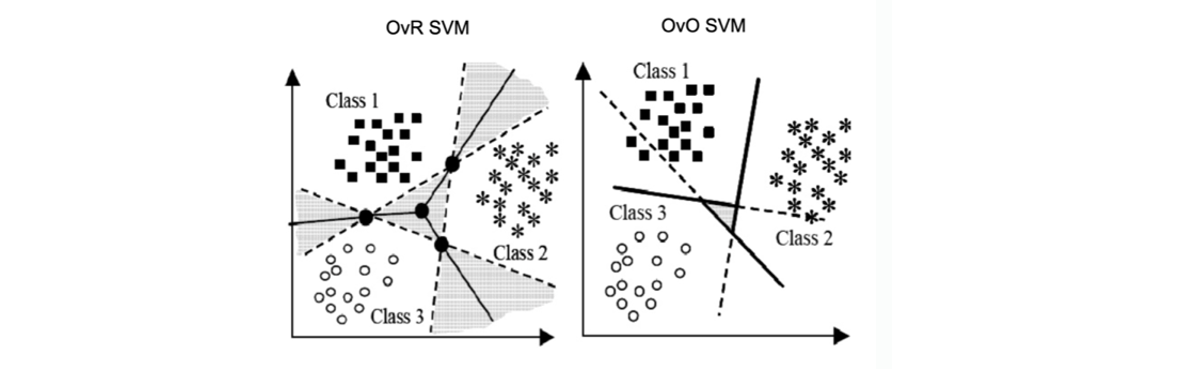
그래서 2가지 방식 모두 문제를 가지게 된다. OvR의 경우에는 특정 데이터가 다른 데이터들에 비해 월등히 적은 경우에는 imbalance 문제가 발생하고, OvO의 경우에도 그럴듯해 보이지만, 하나씩 쌍들에 대해서 계산을 하기 때문에 computaionally expensive하다는 문제가 있다. 그리고 둘 다 다음과 같이 회색 공간에서는 class를 정확하게 판단할 수 없다는 문제도 존재한다.

Approach 3: WW-SVM (by Weston and Watkins)

이러한 문제들을 해결하고자 WW-SVM이 1999년도에 제안되었다. 이 방법은 OvR SVM의 imbalance 문제와 OvO SVM의 local-view 문제를 해결하려고 했다. 자세한 내용은 넘어가도록 하겠다.

Are We Done with SVM?

이러한 노력들에도 불구하여 여전히 SVM에는 limitation이 존재한다. 각 SVM이 hyper plane에 대응이 되고, 이 hyper plane은 class를 나눌 수 있다. 그러나, 데이터가 항상 linearly seperable하지는 않다. 다음과 같이 linearly seperable한 경우에는 하나의 hyper plane으로 정확히 class를 나눌 수가 없다. 이러한 문제를 해결하기 위해서 binary SVM에서는 slack variable 등으로 해결해보기도 했으나, 이번에는 다른 접근을 해보려고 한다. 바로 kernel trick이다. Kernel을 사용하면 linearly seperable하지 않은 데이터들에 대해서 더 많은 featuer을 추출할 수 있고, 그러면 데이터를 feature space에서 linearly seperable하게 만들 수 있다.
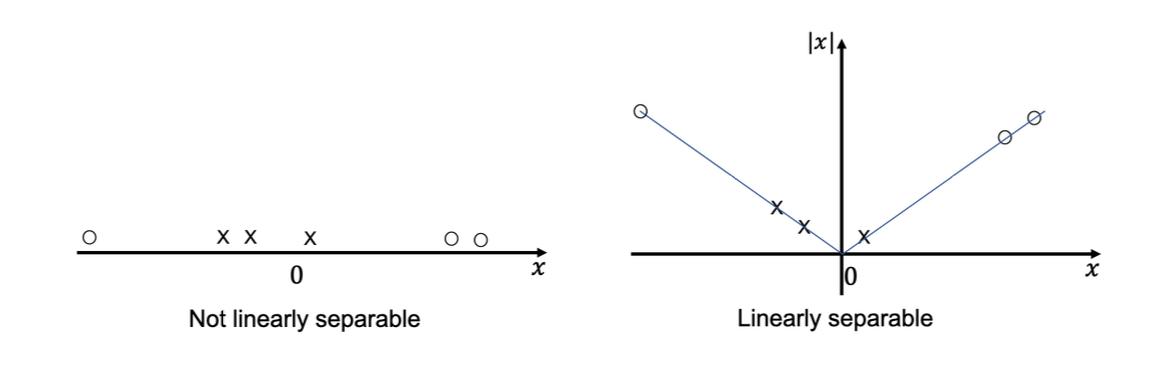좌측의 데이터를 보도록 하자. 0 주변에는 class x가 있고 다른 범위에는 class o가 있다. 이 데이터들은 linearly separable하지 않아서 어떠한 하나의 hyper plane을 그려도 데이터들을 정확하게 나눌 수 없다. 그래서 우측과 같이 다른 feature을 추가하여 차원을 늘리게 되면 데이터들을 feature space에 나타낼 수 있고 하나의 선만으로도 데이터를 나눌 수 있게 된다. 그래서 만약 데이터가 linearly separable 하지 않아도 featuer를 추가하여 차원을 늘려 linearly separable하게 만드는 것이 가능하다. 유용한 feature을 찾는 것이 데이터들을 더욱 잘 나눌 수 있도록 해준다. 보통 이러한 feature들은 수동으로 feature function을 만들어주는데, 그럴 필요 없이 kernel trick을 사용하면 더욱 효과적이게 된다.

Dual Problem of Binary Soft-Margin SVM

Kernel trick을 이해하고 왜 이러한 방식이 흥미로운지 이해하기 위해서 binary soft-margin SVM을 다시 보도록 하자. KKT condition을 사용해서 다음과 같은 dual problem을 만들 수 있다.

\operatorname*{max}_{\alpha} -\frac{1}{2}\sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j \phi^T(x_i)\phi(x_j) + \sum_{i=1}^{N} \alpha_i

s.t. \quad \sum_{i=1}^N \alpha_i y_i=0, \quad 0\leq\alpha_i\leq C \quad \forall i=1,...,N

이 식에서 objective function을 자세히 보면 $\alpha$ 는 maximization해야 하고 $y$ 는 데이터셋으로부터 주어지게 되고 $\sum_{i=1}^N\alpha_i$ 도 variable이다. 우리가 주목해서 봐야할 부분은 $x$ 와 관련이 있는 $\phi^T(x_i)\phi(x_j)$ 다. 우리는 정확한 $\phi^T(x_i)$ 나 $\phi^T(x_j)$ 의 값들은 필요하지 않고 오로지 $\phi^T(x_i)\phi(x_j)$ 내적의 결과만이 필요하다. 즉, 우리는 feature vector에 대해서는 알 필요가 없다. 그래서 이들을 대신하여 $\kappa (x_i,x_j)$ 라는 kernel을 사용할 것이다. 그리고 이것이 kernel trick이다.

Kernel Trick

Kernel trick은 정확한 feature vector과 비교하여 많은 장점을 취할 수가 있다. 각각의 데이터에 대해서 feature를 정확하게 계산하지 않기 때문에 computational cost를 줄일 수 있다. 다음과 같은 feature function은 계산할 양이 엄청나게 많다.

\phi(x) = [1, x_1, x_2, ..., x_1^2, x_1x_2, x_1x_3,...,x_1^3,x_1^2x_2,...]^T

만약 kernel을 대신 사용하게 된다면 이러한 방대한 계산을 진행할 필요가 없다. 그리고 kernel을 사용하게 되면 어떠한 scalar 값을 사용하는 것이다.

Dual Objective Revised

다시 이전의 binary soft-margin SVM의 dual problem에서 이전에는 feature function $\phi$ 를 사용했지만, 이제는 kernel $\kappa(x_i,x_j)$ 를 사용하면 된다.

\operatorname*{max}_{\alpha} -\frac{1}{2}\sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j \kappa(x_i,x_j) + \sum_{i=1}^{N} \alpha_i

s.t. \quad \sum_{i=1}^N \alpha_i y_i=0, \quad 0\leq\alpha_i\leq C \quad \forall i=1,...,N

이렇게 kernel을 사용하면 training 동안 더이상 feature map에 대해서 생각할 필요가 없어진다.

Kernels - Least Square with Gradient Descent

이러한 kernel method는 input 간에 inner product를 이용하는 ML 알고리즘들에 대해서 사용이 가능하다. 그 중에서도 least square method에서 gradient descent step에서 사용이 가능하다. 원래 식은 다음과 같다.

\theta = \theta + \eta\sum_{n=1}^{N}(y_n-\theta^T\phi(x_n))\phi(x_n)

여기서 $\theta$ 는 만약 $\theta$ 의 초기값이 0일 때, $\phi(x_1),...,\phi(x_N)$ 의 linear combination이다.

\theta=\sum_{n=1}^{N}\alpha_n\phi(x_n)

그래서 update step을 적어보면 다음과 같다.

$\theta$
$= \theta + \eta\sum_{n=1}^{N}(y_n-\theta^T\phi(x_n))\phi(x_n)$
$=\sum_{n=1}^{N}\alpha_n\phi(x_n) + \eta\sum_{n=1}^{N}(y_n-\theta^T\phi(x_n))\phi(x_n)$
$=\sum_{n=1}^{N}(\alpha_n + \eta(y_n-\theta^T \phi(x_n)))\phi(x_n)$

그래서 $\alpha_n$ 은 이제 다음과 같이 정의가 된다.

\alpha_n = \alpha_n + \eta(y_n-\theta^T\phi(x_n))

그러면 이제 $\theta=\sum_{n=1}^{N}\alpha_n\phi(x_n)$ 로 $\theta$ 로 바꿔주게 되면 다음과 같다.

\alpha_i = \alpha_i + \eta(y_n-\sum_{j=1}^N \alpha_j\phi(x_j)^T\phi(x_i))

따라서,

\alpha_i = \alpha_i + \eta(y_n-\sum_{j=1}^N \alpha_j\kappa(x_i, x_j))

Properties of Kernels

Kernel은 ML 알고리즘에 있어서 굉장히 유용하게 사용이 된다. 이번 내용에서 가장 중요한건 kernel을 왜 사용하는지 이해하는 것이다. 수동으로 조작하는 feature function 대신에 kernel function을 사용할 수 있다. 그러면 이러한 kernel의 property는 어떠한 것이 있을까?

Valid kernel이 되기 위해서 필요충분 조건으로는 kernel matrix가 symmetric positive semi-definite여야 한다는 것이다. Kernel matrix는 $N \times N$ 의 차원을 가지고, 여기서 N은 데이터의 개수에 해당한다. 원래 feature function의 inner product가 symmetric하기 때문에 symmetric 하다는 것은 쉽게 받아들일 수 있을 것이다. 그래서 $\kappa(x_i,x_j) = \kappa(x_j,x_i)$ 가 된다. 더 중요한 것은 positive semi-definite이다.

Kernels as Similarity Metrics

지금부터는 kernel function을 어떠한 것을 선택해야 하는지 유명한 것들에 대해서 알아보려고 한다. 직관적으로 $\phi(x_i)$ 와 $\phi(x_j)$ 가 서로 가까워 지면, feture vector의 inner product인 $\kappa(x_i,x_j)$ 는 커지게 된다. 또한 만약 $\phi(x_i)$ 와 $\phi(x_j)$ 가 서로 orthogonal하다면, $\kappa(x_i,x_j)$ 가 작아지게 될 것이다. 그래서 우리는 kernel을 feature function들 간에 얼마나 유사한지 측정할 수 있는 metric으로도 생각할 수 있다. 가장 많이 사용하는 kernel은 다음과 같이 Gaussian kernel이다. 우리는 이 kernel을 radial basis function(RBF)라고도 부를 수 있다.

\kappa(x_i,x_j)=exp(-\frac{\|x_i - x_j\|^2}{2\sigma^2})

만약 $x_i=x_j$ 라면, $\kappa(x_i,x_j)$ 는 최대가 될 것이고 그 값은 1이 된다. 만약 $\|x_i-x_j\|$ 가 커지게 된다면, $\kappa(x_i,x_j)$ 는 0에 수렴하게 된다. 이는 굉장히 자연스러워 보인다.

Example: Polynomial Kernel

이러한 kernel 외에도 다른 kernel들을 생각해 볼 수 있다. 또 유명한 kernel로는 degree가 P인 polynomial kernel이 있다.

\kappa(x_i,x_j)=(x_i^Tx_j +1)^P = \phi(x_i)^T\phi(x_j)

만약 $x=[x_1,x_2]^T$ 고 P가 2인 경우에 원래 feature function은 다음과 같다.

\phi(x) = [1,\sqrt{2}x_1, \sqrt{2}x_2, \sqrt{2}x_1x_2,x_1^2,x_2^2]^T

이러한 function은 연산이 오래 걸리기 때문에 바로 kernel을 사용하는 것이 훨씬 빠르다. Kernel을 보면 inner product할 때 d차원의 데이터라고 하면 $O(d)$ 만큼 필요하고 1더하고 p제곱해주는 과정까지 해도 전체적으로 $O(d)$ 만큼이 필요하다. 반면 feature function은 $O(d^P)$ 만큼이 필요하다. P가 커질수록 feature function의 연산량이 훨씬 많아지게 된다.