
오늘날 유명한 neural model에 관해서 볼 것이다. Linear model 말고 neural network를 왜 사용하는지에 대해서 중점적으로 보려고 한다.
Loss Functions for Binary Classification
우선 binary classifcation에서 사용되는 loss function들을 보려고 한다. 다음의 loss function들을 보면 모두 2개의 항으로 구성되어져 있다.
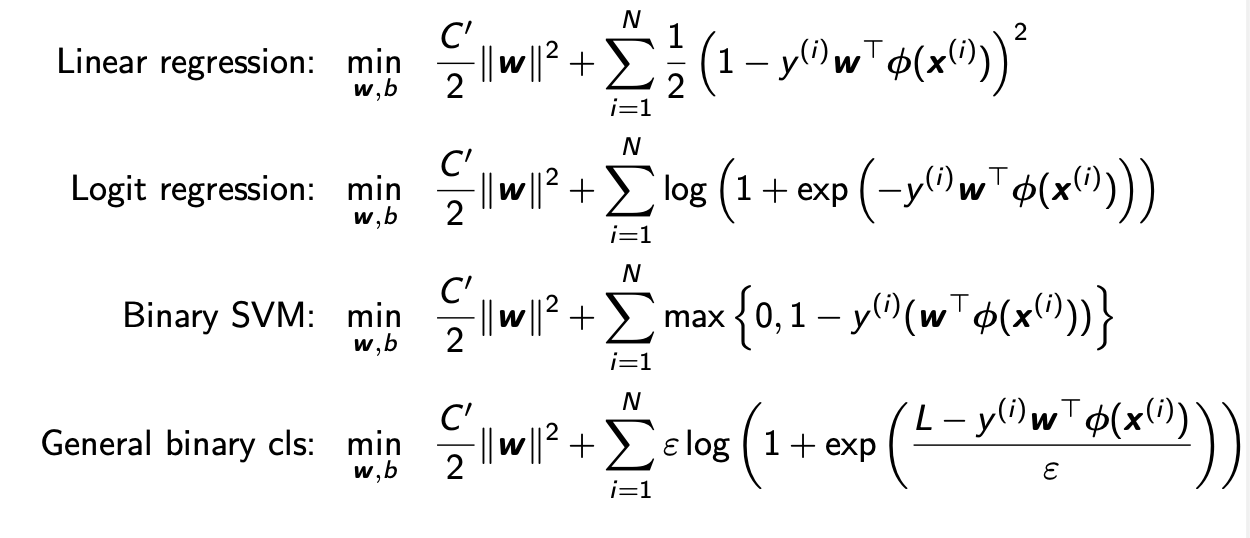 첫번째 항은 overfitting 문제를 피하기 한 regularization을 위해서 존재한다. 그리고 중요한 것은 뒤에 있는 두번째 항이다. 이들은 모두 얼마나 distributed 되어있는지 등에 관한 modeling을 위한 것이다. 보통 는 true label을 의미하고, 는 우리의 prediction을 의미하며, 이는 feature들의 linear combination이다.
첫번째 항은 overfitting 문제를 피하기 한 regularization을 위해서 존재한다. 그리고 중요한 것은 뒤에 있는 두번째 항이다. 이들은 모두 얼마나 distributed 되어있는지 등에 관한 modeling을 위한 것이다. 보통 는 true label을 의미하고, 는 우리의 prediction을 의미하며, 이는 feature들의 linear combination이다.
Using Parameterized Feature
이들은 feature extraction을 통해서 generalization 될 수 있다. Feature extractor로 parameter 를 사용한다.
 그래서 뿐만 아니라 feature extractor 또한 optimization 할 수 있다.
그래서 뿐만 아니라 feature extractor 또한 optimization 할 수 있다.
More General Framework
그리고 이는 한번 더 generalization 될 수 있다.
 대신에 parameter 를 가지는 general function 를 사용할 수 있다. Neural network를 사용하는 것은 가 parameter 를 가지는 neural network가 되는 것을 의미한다.
대신에 parameter 를 가지는 general function 를 사용할 수 있다. Neural network를 사용하는 것은 가 parameter 를 가지는 neural network가 되는 것을 의미한다.
Neural Network for Function Approximation
그래서 neural network는 perceptron, convolution, activation function, maximum/average pooling, soft-max layer, dropout 등의 component로 구성되어진 function model의 power set이다. 이번 내용의 핵심은 이러한 component들을 이해하는데 있다. 이 중에서도 perceptron과 activation function을 중점적으로 이야기해보려고 한다.
Linear Binary Classification
Perceptron에 대해서 알아보기 전에 linear binary classification에 대해서 remind 해보려고 한다. Linear discriminant function은 와 같은 형태를 가지게 된다. 는 input 의 linear combination으로 되어있다. 그러면 linear binary classifier는 lable에 대응되는 우리의 prediction을 로부터 결정한다. Linear binary classification에서는 이러한 방식으로 hyper plane을 통해서 decision boundary를 결정하게 된다.
Perceptron
위에서 본 model이 neural network에서는 perceptron, 혹은 neuron이 된다. 인간의 뇌에 존재하는 neuron은 feature 를 담당하는 수많은 receptor들을 가지고 있다. 그리고 이것들로부터 signal을 보내게 되는데 이 signal이 neural network에서 가 된다. 그리고 이 signal은 특정 threshold가 넘게되면 전송이 되고, 여기서 threshold는 가 맡게 된다. 그래서 input의 weighted sum이 보다 큰 경우에만 neuron이 활성화되는 것이다. 그러면 output으로 1이 전송이 된다. 반대 경우에는 output이 0이 될 것이다. 그래서 이렇게 linear classification model이 perceptron, 혹은 single layer neural network로 해석이 되는 것이다.
그러면 만약, 이 모델이 주어졌을 때, 는 어떻게 train이 되어지게 될까? 오래된 논문에서는 mistake-driven 방식으로 train이 되었고, linearly separable한 데이터에 대해서는 convergence가 보장이 된다고 이야기했다. 여기서 linearly separable하다는 것은 모든 데이터가 하나의 linear model로 에러가 0으로 보장할 수 있도록 완벽하게 classification 된다는 것을 말한다.
Perceptron Criterion
Optimal, 혹은 good perceptrion이라는 것은 에러가 0인 상태를 말한다. 이는 training dataset에 있는 모든 데이터가 정확하게 classification 되는 것이다. 그래서 perceptron criterion은 완벽한 classifction을 의미하며, 다음과 같이 나타낼 수 있다.
단순하게 b는 무시하고 가도 된다. Target value 이 1이나 -1이라고 가정하고, 각각의 데이터에 대해서 우리는 true label 이 prediction 과 같다라는 것을 보장하고 싶다. 만약 이면, 우리는 을 원하고 이는 임을 말해준다. 그리고 만약 이면, 우리는 을 원하고 이는 임을 말해준다. 두 경우 모두에 대해서 과 의 곱이 항상 양수가 되는 것을 볼 수 있다. 그래서 우리는 위와 같이 perceptron criterion을 나타낼 수 있게 된 것이다. 그리고 우리는 이러한 상황이 보장되기를 원한다.
Optimization for Perceptron Criterion
이제 를 train하기 위해서 다음의 loss function을 생각할 수 있다.
Perceptron criterion은 위와 같이 object function이 최소화되도록 만든다. 즉, 모든 곳에서 면서 그 값은 작아지기를 원한다. 그래서 이 loss function을 최소화하기 위해서 우리는 gradient descent를 생각할 수 있다.
The gradient of is
which leads the following gradient descent update (based on only mistakes)
그래서 이 알고리즘을 mistake-driven 알고리즘이라고 말한다.
Perceptron Learning: Stochastic Gradient Descent
최근에는 데이터의 양이 엄청나게 많아졌다. 그래서 이러한 경우에 stochastic gradient descent를 생각할 수도 있다. 먼저 random sampling을 통해서 데이터를 무작위로 선택한다. 그리고 선택이 된 데이터들로 부터 잘못 분류가 된 데이터 하나에 대해서는 업데이트를 진행해준다.
이러한 방식을 convergence 될 때까지 계속해서 반복해주면 된다.
Limitation of A Single Perceptron
Convergence는 가 0 loss를 가지는 linearly separable 데이터에 대해서는 보장이 되어진다. 그러나 이러한 방식에는 분명한 limitation이 존재한다. 만약 우리가 linearly separable 데이터를 가지지 못한다면, perceptron은 converge 할 수 없게 된다. 현실에서는 linearly non-separable한 데이터가 어디에나 존재한다. 다음의 예시를 보도록 하자.
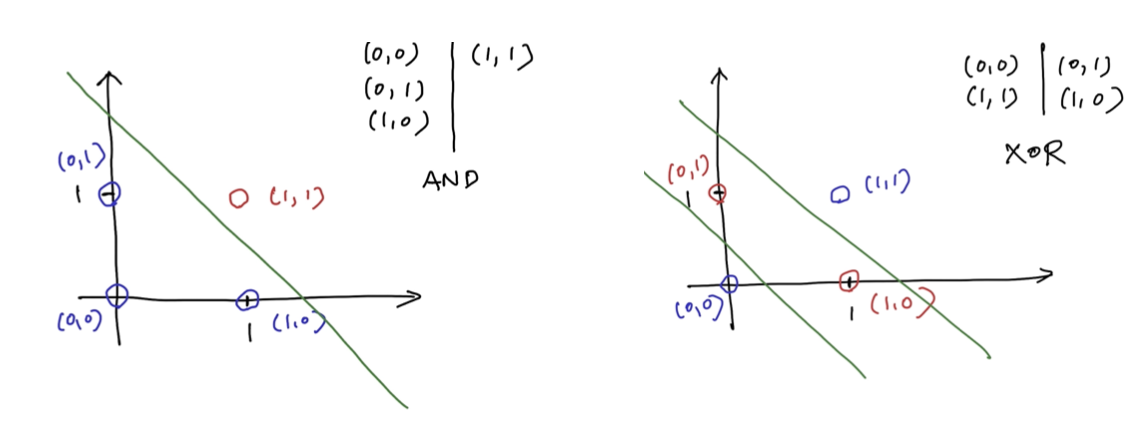 And 연산자 같은 경우 모두 1인 경우에 해당하기 때문에 linearly separable하다. 반면 XOR은 그렇지 않다. 하나의 선으로 나눌 수가 없어 error가 존재하게 된다. 이러한 부분이 single perceptron의 한계가 된다. 이러한 single perceptron의 한계를 극복하기 위해서 multi layer perceptron이 등장하게 된다.
And 연산자 같은 경우 모두 1인 경우에 해당하기 때문에 linearly separable하다. 반면 XOR은 그렇지 않다. 하나의 선으로 나눌 수가 없어 error가 존재하게 된다. 이러한 부분이 single perceptron의 한계가 된다. 이러한 single perceptron의 한계를 극복하기 위해서 multi layer perceptron이 등장하게 된다.
Two Perceptrons
Multi layer perceptron(MLP)는 단순히 perceptron을 여러 층으로 사용하겠다는 것이다. 바로 위의 예시에서 하나의 perceptron이 AND나 OR 연산자에 대해서는 수행이 가능한 것을 볼 수 있었다. 만약 ab라는 하나의 AND 연산자는 하나의 perceptron으로 가능하다. 하지만 여기에 하나가 추가되어 (ab)a와 같은 경우에는 2개의 perceptron이 필요하게 된다.
Combining Perceptrons
그러면 이제 위에서 하나의 perceptron으로 해결하지 못했던 XOR 연산자를 다시 보도록하자. 이 경우에 이제는 2개의 AND와 1개의 OR을 수행하는 perceptron의 조합을 통해서 XOR을 수행할 수 있다.
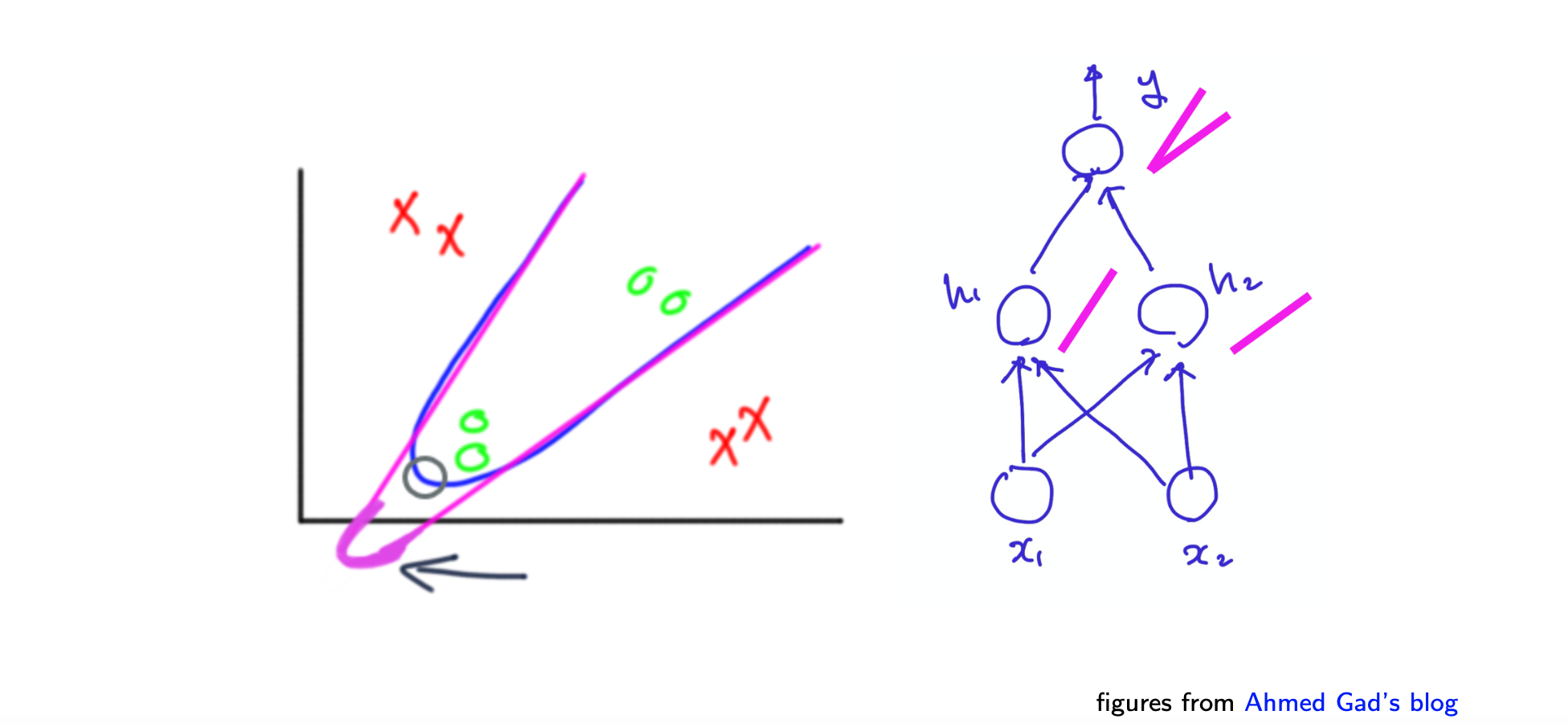
이렇게 perceptron을 여러개 조합해서 multi layer perceptron을 만들게 되면 더욱 다양한 데이터에 적용이 가능해진다. 조합을 어떻게 하는지에 따라 비슷하지만 다른 데이터에 적용이 가능하다.
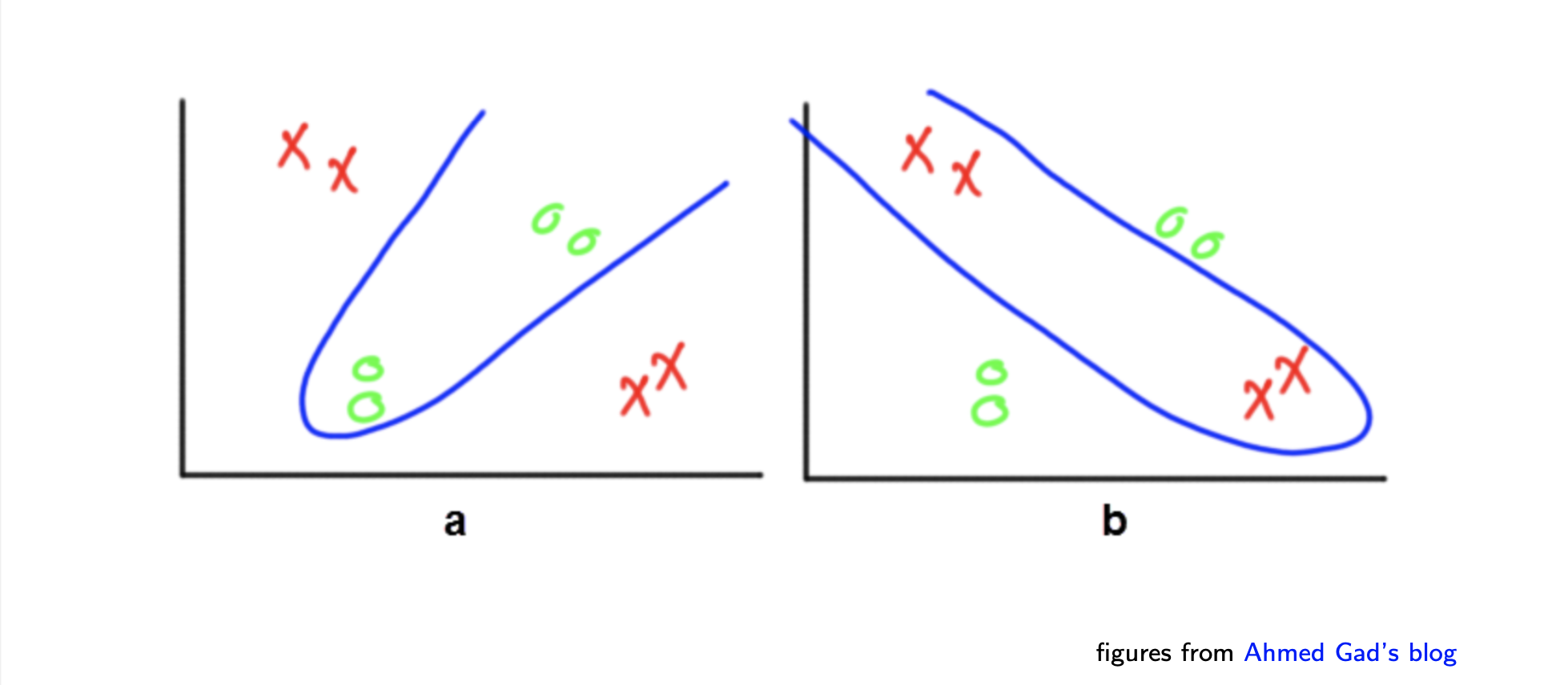 그러면 이제 다음과 같이 좀 더 복잡한 경우를 보도록 하자.
그러면 이제 다음과 같이 좀 더 복잡한 경우를 보도록 하자.
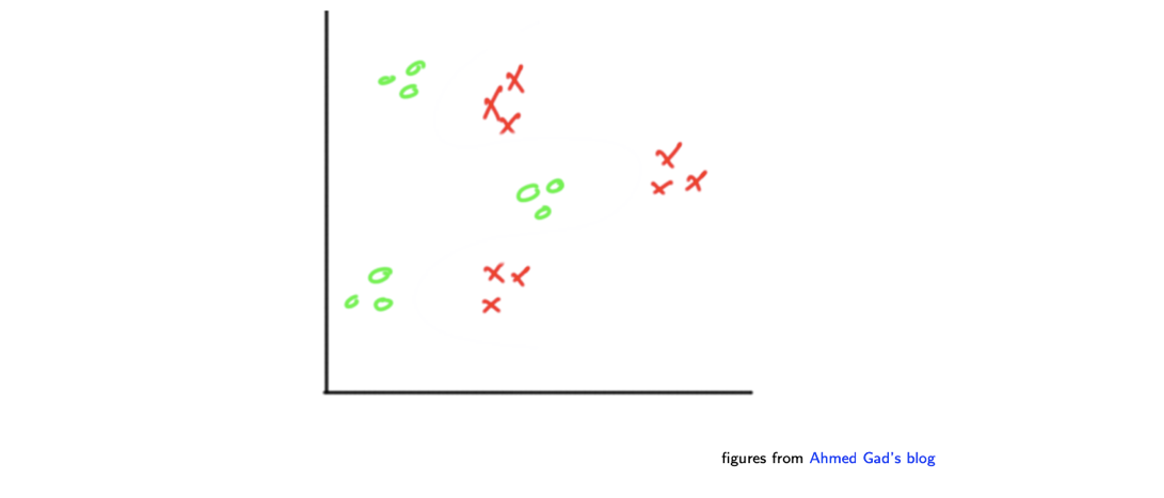
이러한 경우에는 다음과 같은 decision boundary를 그리는 것이 목표가 될 것이다.
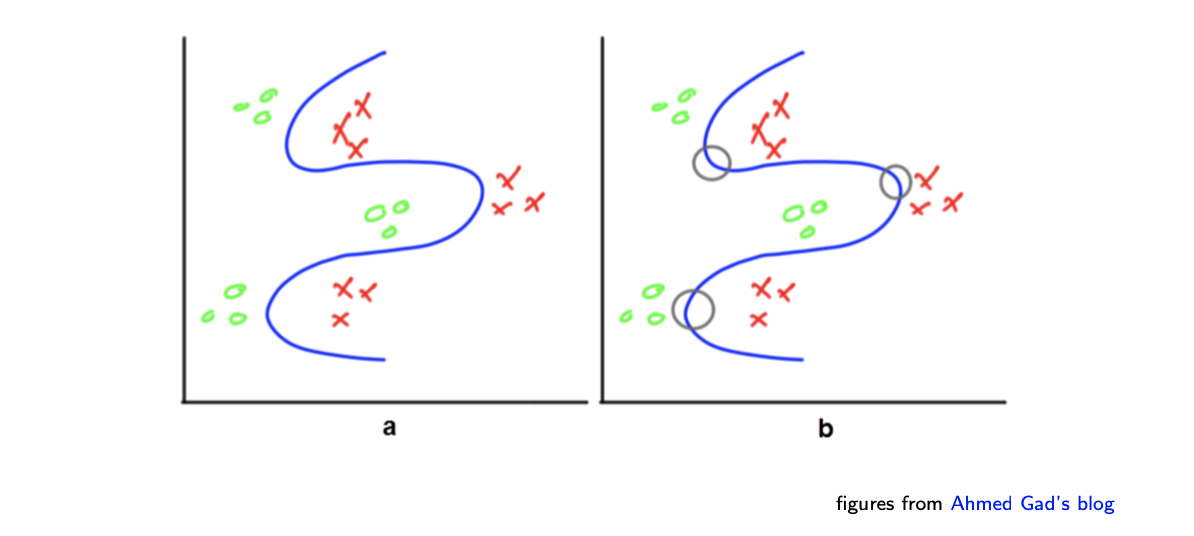 이렇게 복잡한 decision boundary는 이제는 MLP를 통해서 쉽게 그릴 수가 있어졌다. 이러한 곡선의 형태를 취하기 위해서 다음의 perceptron들이 조합을 이루게 된다.
이렇게 복잡한 decision boundary는 이제는 MLP를 통해서 쉽게 그릴 수가 있어졌다. 이러한 곡선의 형태를 취하기 위해서 다음의 perceptron들이 조합을 이루게 된다.
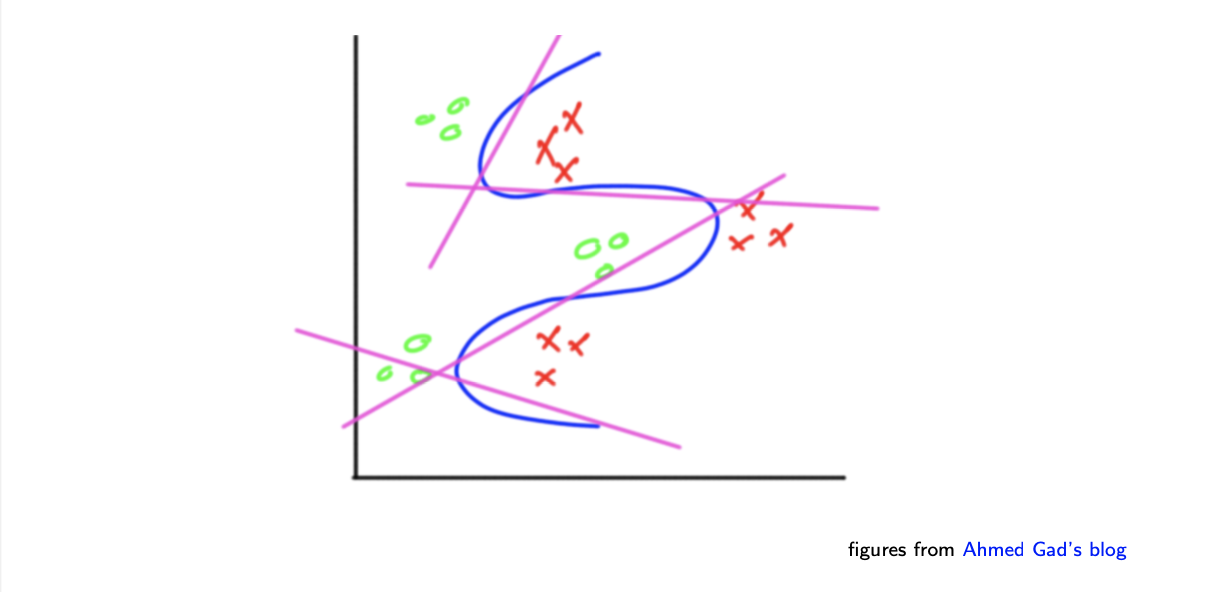
먼저 하나의 layer에 위와 같이 4개의 perceptron을 구성해준다.
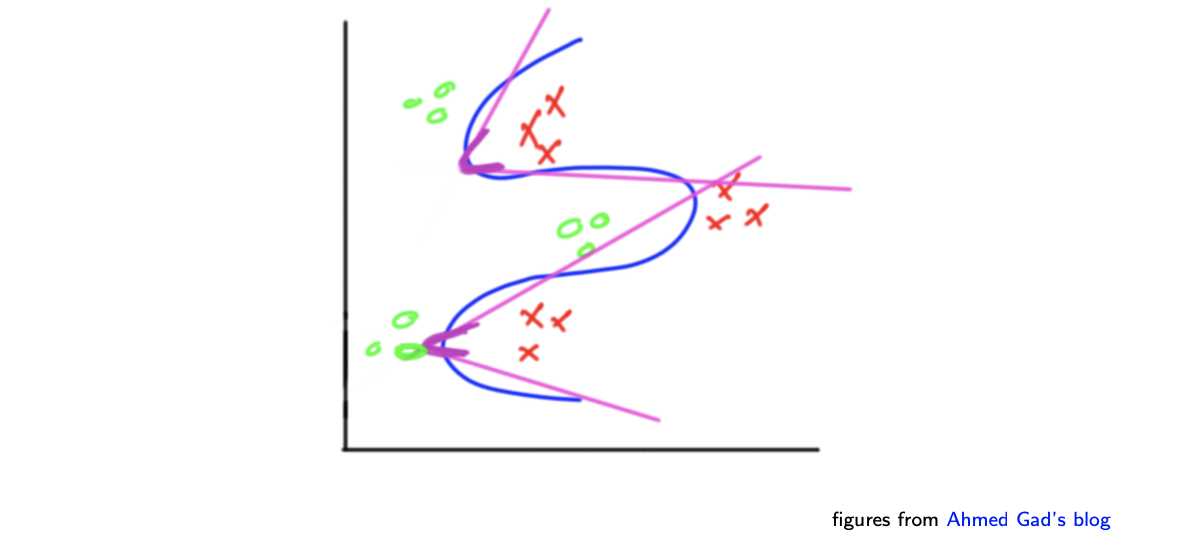
다음으로는 하나의 layer를 추가해서 2개씩 연결해주는 perceptron을 구성해준다.
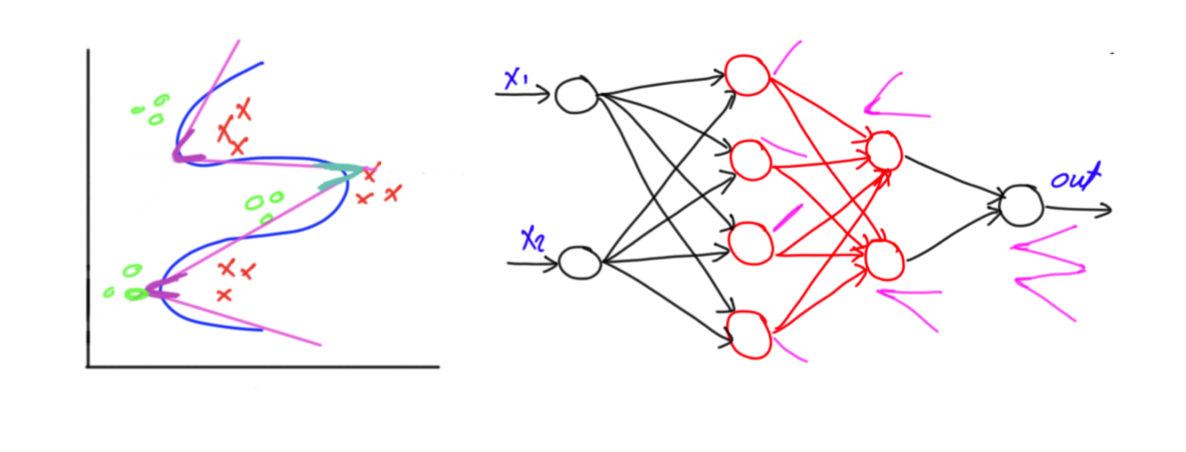 우리가 원하는 것은 binary classification이다. 그래서 마지막으로 하나의 layer를 더 추가해서 최종적으로 연결해주는 perceptron을 구성해준다. 이렇게 되면 총 3개의 layer만으로 decision boundary를 결정할 수 있게 되었다. 오른쪽은 MLP를 graphical하게 나타낸 것이다. 신기하게 각각의 perceptron은 여전히 linear model을 나타내게 된다.
우리가 원하는 것은 binary classification이다. 그래서 마지막으로 하나의 layer를 더 추가해서 최종적으로 연결해주는 perceptron을 구성해준다. 이렇게 되면 총 3개의 layer만으로 decision boundary를 결정할 수 있게 되었다. 오른쪽은 MLP를 graphical하게 나타낸 것이다. 신기하게 각각의 perceptron은 여전히 linear model을 나타내게 된다.
Universal Approximation Theorem
이론적으로 이러한 MLP는 한계가 존재하지 않는다. 그리고 이를 universal approximation theorem이라 한다. 어떠한 continuous function이 주어지더라도 우리는 항상 quantizing function에 의해서 approximation을 찾을 수 있다. Quantization으로 부터의 accuracy loss는 으로 bounded 된다. 그리고 이 quantization에 대해서 우리는 항상 대응되는 neural network를 찾을 수 있다. 이는 input과 output의 차원이 어떠한 경우에도 성립이 된다.
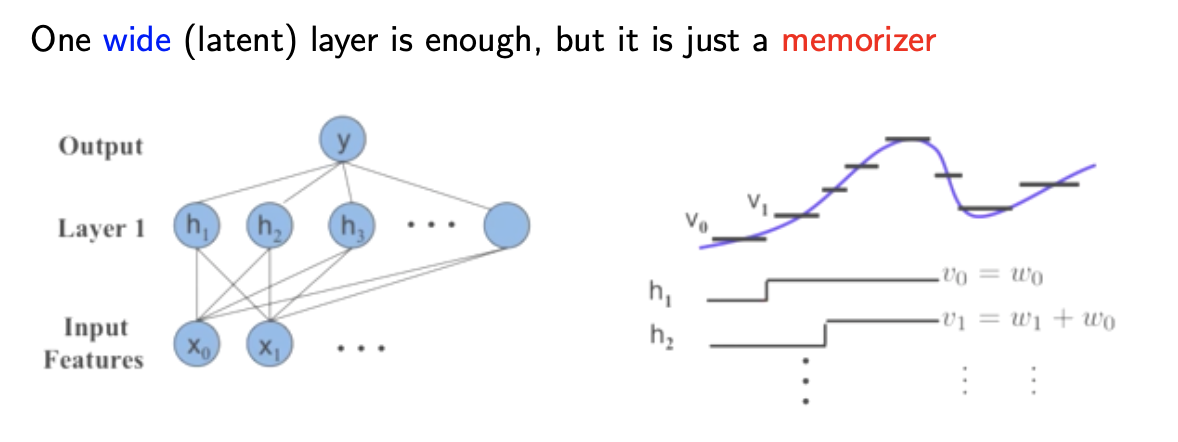
Deep Learning: A Number of Composition of Functions
Deep learning의 영역에서는 넓고 얕은 neural network보다는 좁고 깊은 neural network를 선호한다. 왜냐하면 layer가 넓다는 것은 앞서 본 memorization 문제가 있으며, layer가 깊을수록 function들의 composition을 다양하게 이용할 수가 있다. Composition of functions은 정말로 중요한 부분이다. 만약 하나의 넓은 layer를 가지고 있다면, composition of functions는 오직 마지막 layer에서만 딱 한번 발생한다. 하지만, 만약 여러개의 layer를 가지고 있다면, 각각의 layer에 대해서 우리는 여러개의 function을 구성할 수 있고, 이렇게 되면 다양하게 표현이 가능해진다. 그러면 우리는 어떻게 MLP를 train 시킬 수 있을까? Deep learning은 differentiable function들로 구성이 되어 있어야 한다. 그래야 우리는 gradient descent와 같은 기법들을 적용할 수 있다.
Activation Function
지금까지 본 perceptron을 다음과 같이 나타낼 수 있다.
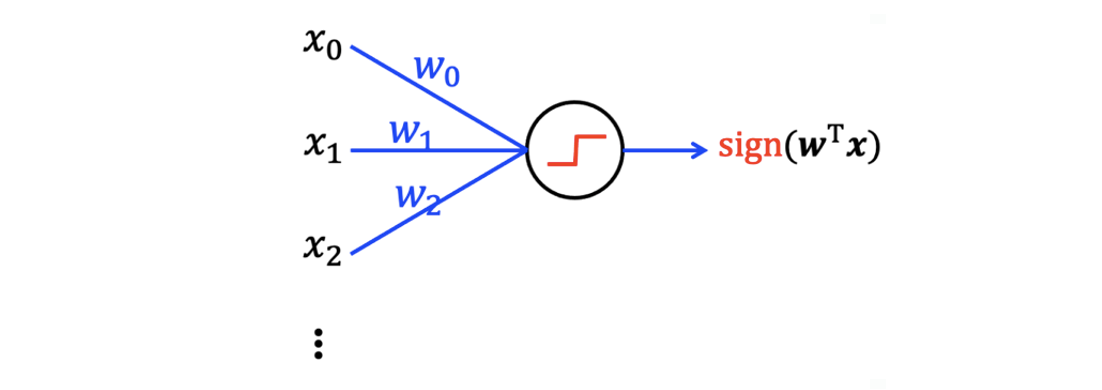 Output은 input signal의 weighted sum의 형태에 step function으로 sign function을 수행해주면 됐었다. 그리고 이는 우리의 뇌에 있는 neuron과 같이 행동한다.
Output은 input signal의 weighted sum의 형태에 step function으로 sign function을 수행해주면 됐었다. 그리고 이는 우리의 뇌에 있는 neuron과 같이 행동한다.
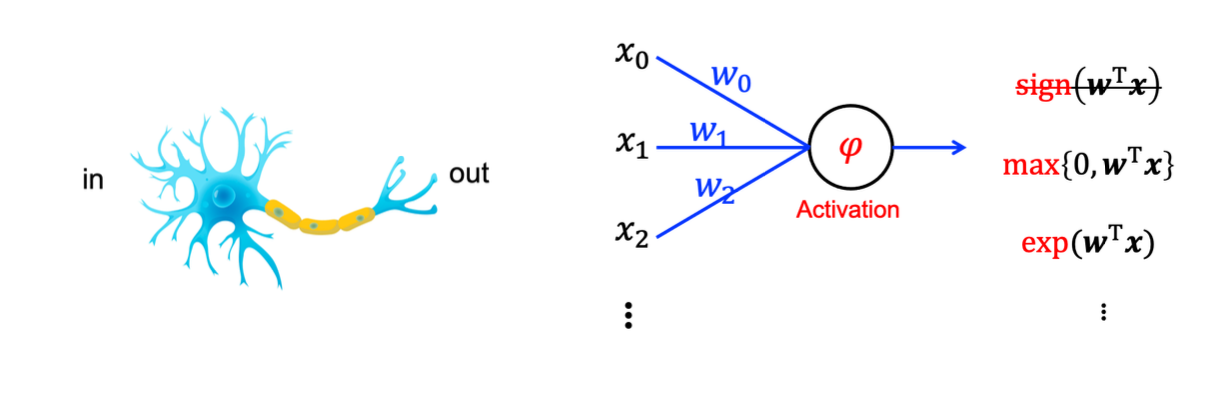 Neuron은 activation policy를 가지게 된다. Non-linear function이 weighted input을 output으로 바꿔주는 역할을 한다. 즉, 하나의 차원에서 다시 하나의 다른 차원으로 보내주게 된다. 우리는 이러한 역할을 하는 function을 activation function이라고 한다. 지금까지는 이 function으로 sign function만을 설명해왔다. 하지만 이제는 이 function에 sign function 뿐만 아니라 max, exp 등과 같은 다른 여러 function들을 사용할 수도 있다. 그리고 가장 많이 사용이 되는 activation function들은 다음과 같다.
Neuron은 activation policy를 가지게 된다. Non-linear function이 weighted input을 output으로 바꿔주는 역할을 한다. 즉, 하나의 차원에서 다시 하나의 다른 차원으로 보내주게 된다. 우리는 이러한 역할을 하는 function을 activation function이라고 한다. 지금까지는 이 function으로 sign function만을 설명해왔다. 하지만 이제는 이 function에 sign function 뿐만 아니라 max, exp 등과 같은 다른 여러 function들을 사용할 수도 있다. 그리고 가장 많이 사용이 되는 activation function들은 다음과 같다.
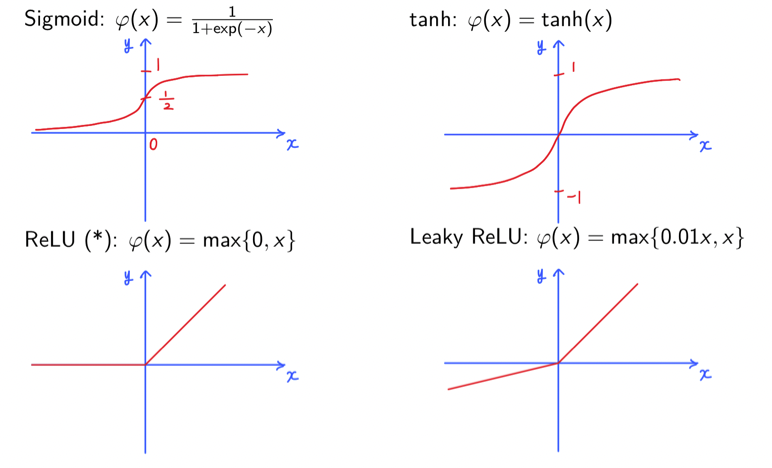 이중에서도 ReLU는 정말로 많이 사용된다. 그리고 leaky ReLU에 있는 0.01이라는 숫자는 음수 범위에 대해서 slope을 결정할 수 있어서 조절이 가능하다.
이중에서도 ReLU는 정말로 많이 사용된다. 그리고 leaky ReLU에 있는 0.01이라는 숫자는 음수 범위에 대해서 slope을 결정할 수 있어서 조절이 가능하다.
Fully Connected Layer
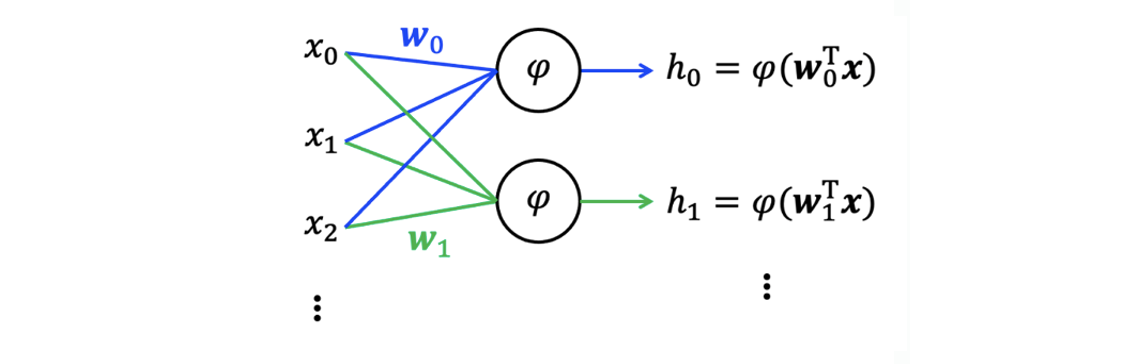 Input layer와 output layer에 있는 모든 node들이 전부 연결이 되어있으면 이를 fully connected layer라고 한다. 그리고 Output 값들을 latent variable이라 한다.
Input layer와 output layer에 있는 모든 node들이 전부 연결이 되어있으면 이를 fully connected layer라고 한다. 그리고 Output 값들을 latent variable이라 한다.
