[기계학습] Neural Networks 2

JAEYOON SIM·2021년 10월 22일

Machine Learning

목록 보기

19/35

How to Train MLP? Backpropagation

MLP를 train 하기 위해서 가장 유명한 방법은 backpropagation이다. 예전부터 사용된 방법이지만 최근에도 많이 사용되고 있다. 먼저 backpropagation의 아이디어부터해서 그 방법이 어떻게 되는지까지 알아보려고 한다. 먼저, 다음과 같은 loss function이 있다고 가정해보자.

L = \sum_{n=1}^{N}\ell(y_n,h_L)

이 Loss function은 각각의 loss function의 합으로 되어있다. 각각의 loss function은 lable $y_n$ 과 neural network output $h_L$ 를 인자로 가지게 된다. 그리고 $h$ 는 neural network의 layer들을 연속적으로 가지게 된다. 다음과 같이 $h_L$ 을 reculsive하게 일반화 할 수 있다. 이전의 결과와 새로운 $W, b$ 를 이용해서 계속해서 output을 만들어나가게 된다.

h_1 = \sigma(W_1x+b_1)

h_2 = \sigma(W_2x+b_2)

\dotsc

h_L = W_Lh_{L-1} + b_{L-1}

결국 마지막에 도달하는 $h_L$ 은 neural network의 prediction이 될 것이다. 결국 Loss function $L$ 을 최소화하는 것이 우리의 목표이고, 이러한 목표를 통해서 neural network를 train하게 된다.

Compute Partial Derivatives

그렇다면 어떻게 train을 시켜 $W, b$ 를 찾을 수 있는 것일까? 예를 들어 하나의 hidden layer를 생각해볼 것이다. 그러면 loss function은 다음과 같게 된다.

L = \sum_{n=1}^N(y_n-w_2\sigma(w_1\,^Tx_n))^2

w_x \in R, \quad w_1\in R^D, \quad x_n \in R^D

$w_2$ 는 scalar, $w_1$ 은 D차원의 column vector, $x_n$ 도 D차원의 column vector이다. 분명하게 하기 위해서 모든 벡터는 기본적으로 column vector로 간주하고 갈 것이다. 우리의 model은 prediction 값으로 $w_2\sigma(w_1^Tx_n)$ 을 계산하고, 이는 ture label $y_n$ 과 같을수록 model이 제대로 train이 된 것이다. 그러기 위해서 우리는 이 2개의 값의 차이를 최소한으로 만들고 싶은 것이다. 그래서 이 loss function은 mean squared error를 사용하려고 한다. Loss function으로 선택되는 function은 이를 최소화하는 $w_1$ 과 $w_2$ 를 찾기 위해서 non-convex optimization을 사용하게 된다. 그래서 이 loss function으로부터 gradient descent를 하기 위해서 우리가 할 일은 단지 모든 parameter에 대해서 partial derivative를 계산해주기만 하면 된다. 그래서 이 계산으로부터 $w$ 값들을 다음과 같이 새롭게 업데이트 시켜주면 된다.

w_1^{\text{new}} = w_1^{\text{old}} \leftarrow \alpha \cdot \frac{\partial L}{\partial w_1}

w_2^{\text{new}} = w_2^{\text{old}} \leftarrow \alpha \cdot \frac{\partial L}{\partial w_2}

이렇게 gradient를 업데이트하고 싶은 parameter에 대해서 구하고 이를 반영하여 새로운 값으로 바꿔주는 gradient descent 과정은 loss를 최소화하는 방향으로 진행이 된다. 그러나 이러한 방법은 일반화시키기에는 무리가 있어서 크게 좋은 방법은 아니다. Loss activation function과 neural network의 어떠한 변화가 있을 때, 우리는 모든 gradient를 다시 써줘야 한다. 이는 computational cost적인 측면에서 expensive하기에 실로 좋지 못하다. 그래서 우리는 gradient를 계산하기 위해서는 더 일반적인 접근 방식이 필요하다. Partial derivative를 계산하는 가장 일반적인 방법은 이제부터 살펴 볼 Back-propagation 알고리즘이다.

Back-propagation

Back-propagation을 이해하기 위해서 간단한 예시를 들어보고자 한다. 이는 neural network는 아니고, 단지 function의 조합들일 뿐이다.
Input은 $x, y, z$ 이고, output으로는 $q, f$ 가 있다. 가장 먼저 $x$ 와 $y$ 를 통해서 latent internal variabel $q$ 를 계산하고, 그리고 이 $q$ 와 $z$ 를 곱해서 $f$ 를 계산할 수 있다. 이제 이해하기 쉽게 숫자를 대입해서 생각해보자. $x, y, z$ 에 값을 대입해서 $q, f$ 를 계산하는 것은 어렵지 않다. 이제 back-propagation을 통해서 input variable에 관하여 function $f$ 를 optimization해주기 위해서 partial derivative를 구해야 한다.
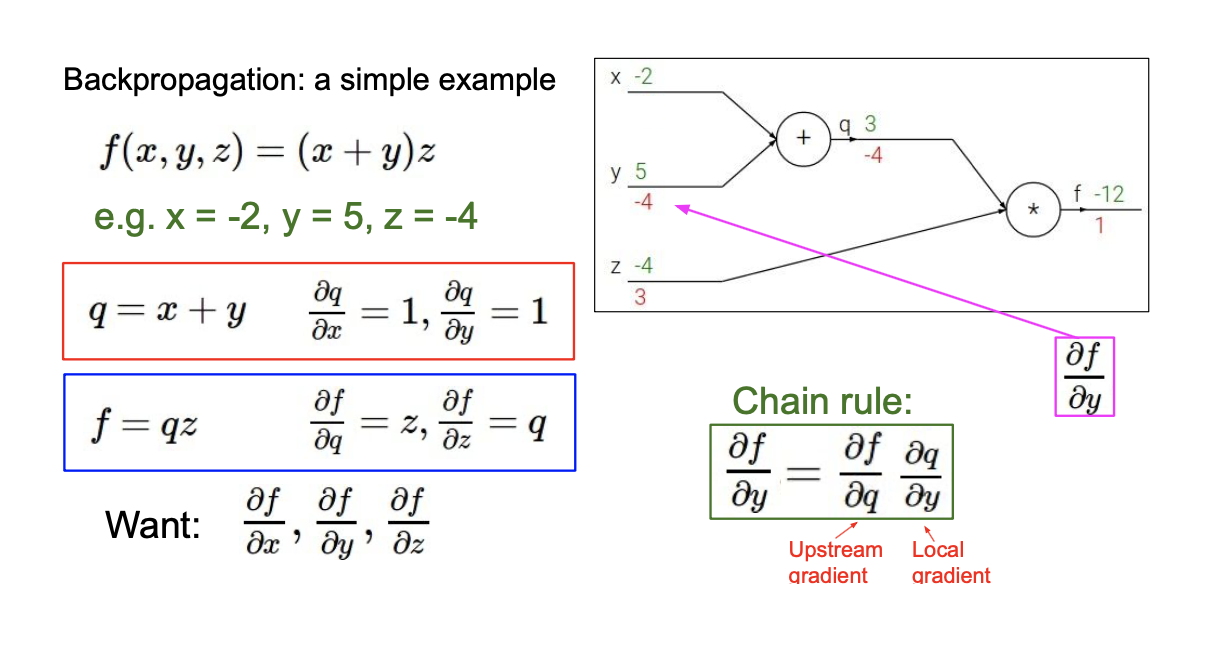우리가 원하는 결과를 구하기 위해서 $q$ 에 관해서도 partial derivative를 구해줘야 한다. 이렇게 중간 과정에 있는 변수들에 대하여 partial drivative를 구한 뒤에 chain rule이라는 것을 통해서 최종적으로 구하고 싶은 것들을 구하면 된다. 이 부분은 크게 어렵지 않은 내용들이다. 한단계씩 미분을 해가면서 chain rule에 따라 곱해주기만 하면 된다. 위의 예시는 매우 특수한 경우이고, 이를 일반화한다면 다음과 같이 할 수 있다.
각 variable의 composition에 대해서 먼저 local gradient를 계산할 수 있다. $z$ 를 local output이라 했을 때, input $x, y$ 에 대해서 partial derivative를 구할 수 있다. 그리고 이 정보들을 토대로 우리가 구하고자 하는 loss function과 각 variable $x, y$ 에 대해서 partial derivative를 구하면 된다. 그래서 chain rule에 의해서 upstream gradient와 local gradient들로부터 downstream gradient를 구할 수 있다.

Neural Networks(con't)

우리가 model을 train하기 위해서 필요한 것은 loss function $L$ 과 1부터 N까지의 모든 $w, b$ 에 관한 partial derivative들이다.

\frac{\partial L}{\partial W_L} = \frac{\partial L}{\partial h_L}\frac{\partial h_L}{\partial W_L}

그래서 neural network에 대해서 생각했을 때, 하나의 neuron에 대해서 local output은 $h_L$ 이고, input이 $W_L$ 이 되고 앞서 chain rule을 적용해 back-propagation을 하고 싶기 때문에 upstream gradient $\frac{\partial L}{\partial h_L}$ 와 local gradient $\frac{\partial h_L}{\partial W_L}$ 을 이용하여 downstream gradient $\frac{\partial L}{\partial W_L}$ 을 구할 것이다.
Layer가 늘어날수록 local gradient를 계속해서 곱해주면 된다. 계속해서 gradient를 구하다보면 우리가 원하는 paramet $w$ 에 대한 gradient를 얻게 될 것이다.

정리하면 $L$ 은 각각의 loss function의 합으로 나타낼 수 있고, 이 loss function의 정확한 값을 계산하기 위해서 각각의 loss function의 gradient를 계산해야 한다. 그러나 현실에서는 데이터의 양이 굉장히 많기에 이는 좋은 방법이 아니다. 그래서 우리는 stochastic gradient descent를 생각할 수 있었다.

Error Functions

지금까지 single perceptron를 보았고, 이에 대해서 표현하는 방식에 한계를 보였었다. 그래서 생각한 것이 multi layer perceptron이었고 간단한 예시들을 통해서 알아보았다. 그리고는 universal approximation을 보았다. 하나의 넓은 hidden layer가 있다고 했을 때, 거의 모든 continuous function으로 approximation 할 수 있다는 것을 알았다. 이는 단지 표현하는데 있어서 좋았던 것이고, 우리가 필요로 했던 것은 어떻게 MLP를 train하는가였다. Universal approximation에서는 표현하는 것에 있어서 충분하다는 것을 알게 되었고, 하나의 parameter를 train하기 위해서 gradient 기반의 방식들을 생각해 볼 수 있었다. 그래서 gradient descent를 수행하기 위해서 연속적인 chain rule에 의해서 계산이 가능했고, 이를 back-propagation이라고 불렀다. 지금부터는 여러 다른 loss function들에 알아보려고 한다.

Supervised learning에서 우리가 필요로 하는 것은 lable이 된 데이터셋과 true lable과 expected lable의 차이를 판단할 수 있는 method이다. 그래서 유명한 error function으로 sqaured error가 있다. 이는 regression task에 매우 유명한 function이다. Mean squared error는 squared error의 평균을 계산하는 것이다. 여기서 L2-norm은 L1-norm이나 cosine similarity 등과 같이 대체할 수 있다. 특히 classification에서는 cross entroy error를 주로 사용한다.

Softmax Layer for Classification

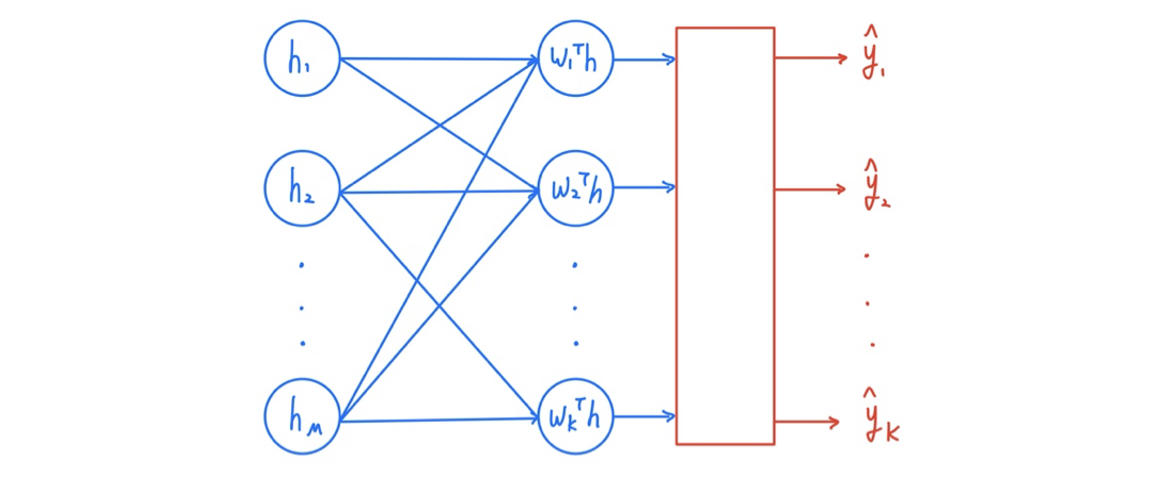어떠한 구조의 architecture를 사용해서 output이 여러개인 neural network를 만들었다고 해보자. 그리고 이 output들은 normalization이 되어 있지 않을 것이다. Classification을 위해서 우리는 모든 output의 합이 1이 되기를 원한다. 그래서 유명한 nomalization 방식 중 하나인 softmax를 이용한 softmax layer를 추가해줄 것이다. 그래서 결과적으로 0에서 1 사이의 확률 값으로 나타낼 것이다. Normalization을 위한 식은 다음과 같이 정의할 수 있다.

\hat{y_k} = \frac{exp(w_k\,^Th)}{\sum_{j=1}^K exp(w_j\,^Th)}

KL Divergence

다른 2개의 distribution $p, q$ 를 비교하기 위해서 KL divergence를 metric으로 사용할 것이다.

KL(p,q) = \sum_xp(x)log\frac{p(x)}{q(x)}

$p$ 는 real distribution이고 $q$ 는 virtual distribution으로 생각하면 된다.

Cross Entropy

우리가 바꾸고자 하는 것은 $q$ 이다. 그래서 우리는 KL divergence로부터 $q$ 에 대한 partial derivative를 구할 것이다. 우선 KL divergence에서 $log$ 항은 마이너스로 나눌 수가 있다. 이렇게 나누었을 때 $q$ 와 상관 없는 항은 $p$ 의 negative entropy라 부르고, 무시할 수 있다. 우리는 오로지 $q$ 와 상관이 있는 항을 최소화는데 집중할 것이다. 그리고 우리는 이 항을 cross entropy라 부를 것이다.

Cross Entropy Error

특히 binary classifcation에 대해서 true distribution을 안다고 하면 이를 one hot vector로 나타낼 수 있다. 그러면 결국 0아니면 1로 정해지게 되어 다음과 같이 cross entropy error를 계산할 수 있다.

\varepsilon = \sum_{n=1}^N [-y_nlog\hat{y_n}-(1-y_n)\,log(1-\hat{y_n})]

이번에는 만약 2가지 경우가 아닌 K개의 class로 classification을 한다면, cross entropy loss를 다음과 같이 계산할 수 있다. $y$ 를 하나의 값만 1로 두고 나머지를 전부 0으로 두어 one hot vector로 표현하면 된다.

\varepsilon= \sum_{n=1}^N \sum_{k=1}^K [-y_{k,n}\,log\, \hat{y}_{k,n}]

Cross entorpy error를 특정 값을 통해서 계산하면 다음과 같이 쉽게 이해가 될 것이다. 어떠한 model이 있고 여기에 tiger, lion, cat에 대한 정보를 받아서 각각에 대응되는 normalized value를 계산해낼 수 있다.
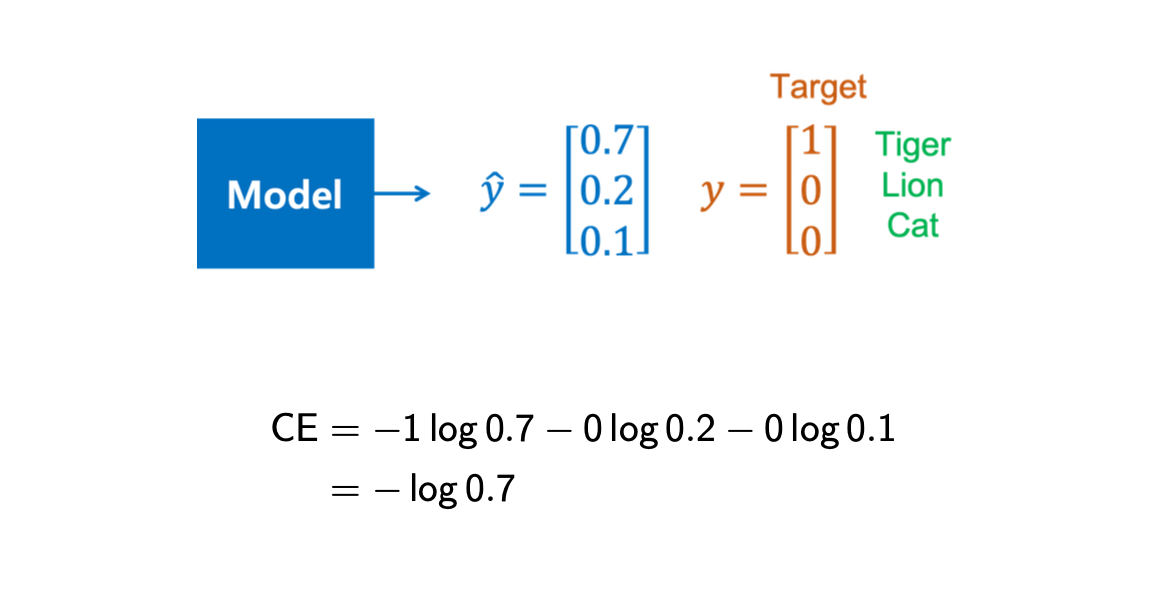이러한 경우에 대해서 실제 true lable에 해당되는 동물이 tiger인 경우에 cross entropy loss를 구할 때, tiger에 대응되는 $log$ 항에 1을 곱해주고 나머지 항에 0을 곱해주면 된다.