[기계학습] Some Insights of Model Selection 1

여러 model과 ML framework에 대해서 지금까지는 supervised learning에 집중했었다. Linear model, perceptron, SVM, neural network 등 많은 modele들에 대해서 알아보았다. 이렇게 많은 model들에 대해서 알고 사용하면 좋지만, 현실에서는 반드시 하나를 선택해야 한다. 그래서 이번에는 이러한 많은 model들 중에서 어떻게 하면 만족스러운 model을 하나 고를 수 있을지에 대해서 이야기해보려고 한다.

How to Build a Good Model?

Image Processing

어떻게 하면 좋은 model을 build 할 수 있을지 알아볼 것이다. 좋은 model을 고르기 위해서 몇가지 예시를 통해서 시작해보려고 한다. Image processing에서 fully connected(FC) layer을 사용할 수 있다. 그렇다면 오로지 FC layer만을 사용하는 것은 좋은 선택일까? 솔직히 여러 관점에서 생각해 보았을 때, 이는 좋은 생각은 아니다. 왜냐하면 model은 모든 데이터를 스스로 기억하는 충분한 능력을 가지고 있다. 그러나 generality나 이미지를 이해하는 intuition이 부족하기 때문이다. 이러한 문제를 극복하기 위해서 한 사례로는 이미지 데이터셋에 hypothesis를 추가하기도 했다. 유명한 hypothesis 중 하나는 이미지가 spational locality를 가지고 있다는 것이다.
Spatial locality란 이미지가 주어졌을 때 이웃하는 픽셀은 비슷한 데이터를 가진다는 것이다. 그리고 FC network를 학습하고자 하는 것은 모든 픽셀들에 대한 correlation이다. 이웃하는 픽셀 사이가 멀리 떨어져 있는 픽셀 사이보다 더 강한 correlation을 가지게 된다. FC network에서는 가까운 픽셀부터 멀리 떨어진 픽셀과의 corrlation도 학습하려고 한다. 이러한 것은 필요해 보일지도 모른다. 실제로는 이미지에서 멀리 떨어진 픽셀과는 보통은 중요한 정보를 가지지 않는다. 그런데도 FC network는 많은 parameter를 학습하려고 한다.

Convolutional Neural Network

Parameter 수를 줄이는 방법으로 convolutional operator는 generality를 높이고 model의 크기를 줄여 convolutional neural network를 정의하게 된다. Convolutional neural network는 다음의 convolutional operator를 수행하게 된다.

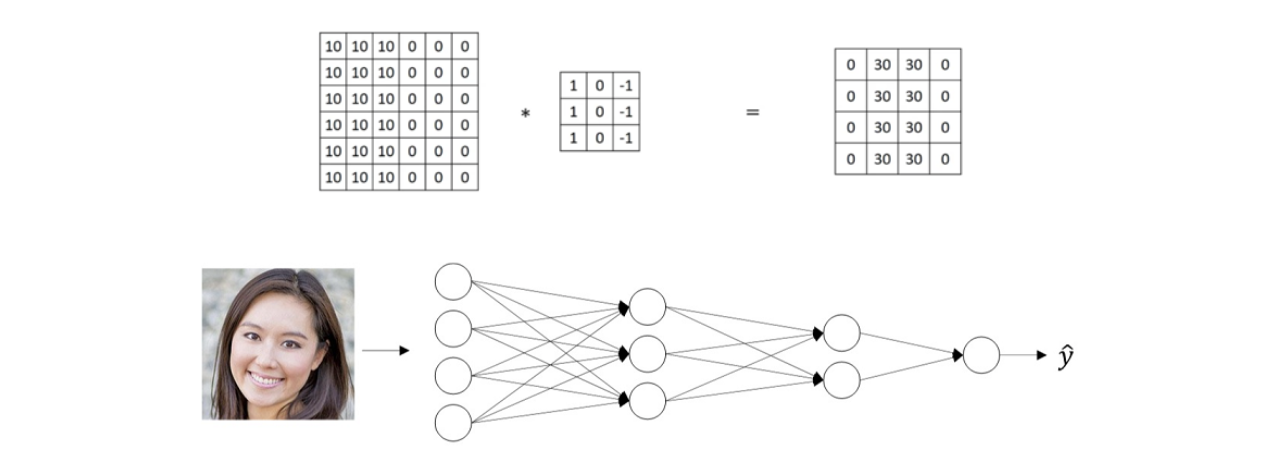2D 이미지는 2차원의 matrix로 해석될 수 있다. 그래서 위와 같이 절반은 10으로 절반은 0으로 된 2차원의 데이터가 있을 때, spatial locality를 학습하기 위해서 filter와 convolution operator를 수행하게 된다. 이 filter가 convolution neural network에서 parameter가 될 것이다. 좌측 상단부터 filter를 이용해서 convolution operator를 수행하게 되면 그 결과 값으로 새로운 matrix가 만들어지게 된다. Convolution operator는 해당하는 위치의 값들을 곱해서 전부 더해줘 하나의 값으로 도달하게 된다. 그렇게 filter를 이동해가면서 같은 연산을 진행해주면 된다.

문제가 있다면 convolution을 하게 되면 dimensionality를 잃게 될 수도 있다. 위와 같이 특정 filter가 주어지고 이미지가 극단적인 10과 0으로 구성되었을 때, 결과는 그 경계선 부근에 큰 값들로 구성이 되었다. 그래서 위의 filter와 같이 filter의 구성에 따라 edge를 검출하거나 특정 부분의 feature를 얻을 수가 있다.
Convolution을 하게 되면 이미지에 대해서 간단한 line과 같은 feature부터 line의 조합으로 이루어진 특정 shape, 그리고 더 나아가 high level의 feature를 얻을 수가 있다. 그래서 convolutional neural network는 조절할 수 있는 filter로 구성이 되어 있어서 filter의 parameter를 업데이트 할 수 있다. 이러한 방식은 좋아보이며 합리적이게 보인다.

Ventral Visual Stream

이러한 모든 것은 인간의 시각 시스템과 같은 hypothesis를 기반으로 하며, 이를 ventral visual system이라고 한다. 우리에 뇌에 대해서 뇌과학자들은 convolution operator와 비슷하게 수행하는 여러 module이 존재한다는 것을 알아냈다.
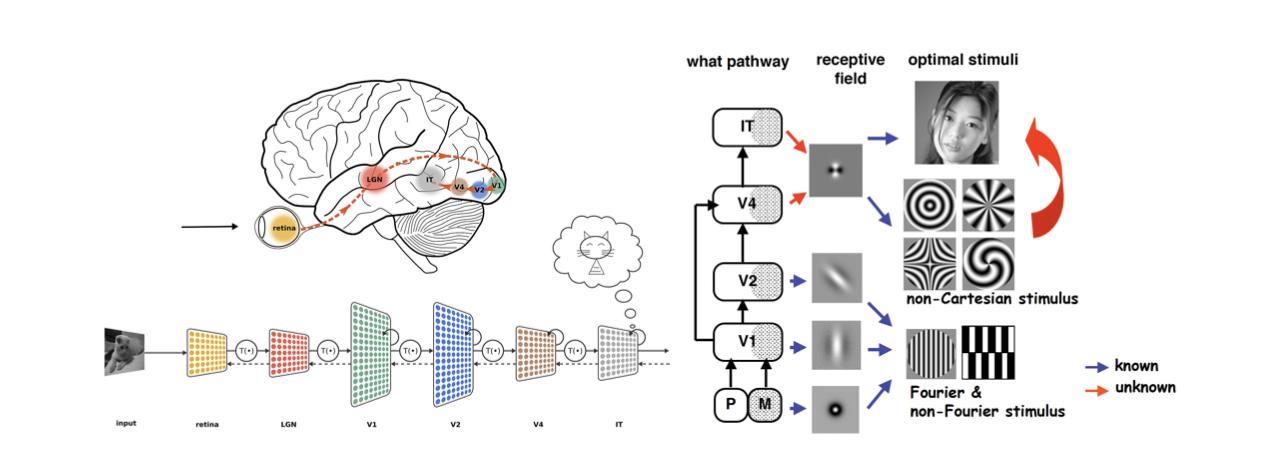눈으로 부터 받아들인 시각 정보는 LGN module로부터 line과 같은 작은 부분을 검출하게 된다. 그렇게 convolution operator를 따라 계속해서 다른 여러 module을 거쳐가게 되는 것이다. 그래서 인간의 뇌와 유사하게 convolution operator는 이미지에 대해서 합리적인 방식으로 보인다.

Convolutional Neural Network(Con't)

이미지는 2차원의 데이터와 2차원의 filter를 사용해서 2차원의 convolution operator가 적합하다. 반면 오디오 데이터와 같이 시계열 데이터는 시간에 따른 진폭으로 되어 있어서 이미지와는 구성이 다르다. 시계열 데이터는 시간에 따른 continuous 정보를 가지게 되어 temporal locality를 가지고 있고, 이 데이터에 대해서 convolution operator를 적용할 수도 있어 보인다. 대신 이러한 경우에는 1차원의 convolution operator를 적용해야 한다. 오디오 데이터를 1차원의 matrix로 생각하고 1차원의 filter를 사용하면 된다. 이렇게 convolutional neural network는 이미지와 오디오, 심지어는 비디오까지 많이 사용되는 선택지가 되었고, 이는 locality의 본질을 이용할 수 있다.

그러나 convolution operator와 같이 간단한 방식은 많은 문제를 가지게 된다. 첫번째로 convolution 이후에 데이터의 크기가 줄어들게 된다. 위의 예시에서 $6 \times 6$이었던 이미지가 $4\times 4$로 줄어들었다. 이는 dimenstionality에서 차이가 생기기 때문에 원래 이미지와 결과 사이의 correspondence를 파악하기 어려워진다. 동시에 이렇게 작은 크기를 가지게 되는 것은 좋은 아이디어는 아니다. Convolution의 결과에 대해서 원래 이미지의 외곽 픽셀들이 가지는 정보가 내부의 픽셀들이 가지는 정보에 비해서 기여하는 바가 적어지게 된다. 왜냐하면 convolution operator에서 코너에 있는 픽셀은 한번만 사용이 되기 때문이다. 반면에 중간에 있는 픽셀은 크기가 3인 filter에 대해서 적어도 6번에서 많게는 9번 사용이 된다. 즉, 중간에 있는 픽셀은 9배나 결과에 기여하는셈이 된다. 물론 보통 이미지에서 중요한 정보는 중앙에 가까울수록 많겠지만, convolution적인 관점에서는 외곽의 정보가 상대적으로 적게 기여하게 되는 것이다. 물론 이러한 imbalance contribution은 확률적일 수 있지만, 이러한 boundary 문제를 해결하기 위해서 zero padding과 같은 기법을 사용하게 된다. 기존의 이미지의 크기를 보존하기 위해서 외곽을 임의의 0이 둘러싸고 있다고 생각하고 convolution을 하는 것이다. 물론 0의 개수도 조절이 가능하다. 이는 filter의 크기를 기반으로 정하는 것이 일반적이다. 0을 추가하게 되면 원래 이미지의 외곽의 픽셀도 같은 횟수로 기여할 수가 있게 된다.

그리고 convolution의 속도를 높이기 위해서 모든 patch에 대해서 연산을 진행하지 않을 수 있다. 위의 예시에서 1칸씩 이동하면서 convolution을 하게 되면 총 16번을 하게 되는데 이러지 말고 3칸씩 이동해서 하면 4번만 할 수도 있다. 보통 high resolution 데이터에 대해서 이렇게 convolution을 조금만 수행하여 속도적인 측면을 해결하기도 한다. 그리고 이렇게 이동하는 칸의 개수를 stride라고 한다. Stride를 키울수록 convolution을 덜 하겠다는 이야기다. 이미지에 대해서 최대한 정보를 많이 사용하겠다고 하면 stride를 1로 설정하면 된다.

Pooling Layer

많은 정보를 가지고 있는 것은 사실 좋은 생각은 아니다. 그래서 많은 정보를 줄이거나 요약하는 방법으로 pooling이 있다. 보통 pooling을 할 때 2가지 선택지가 존재한다. 하나는 max pooling이고 다른 하나는 average pooling이다.
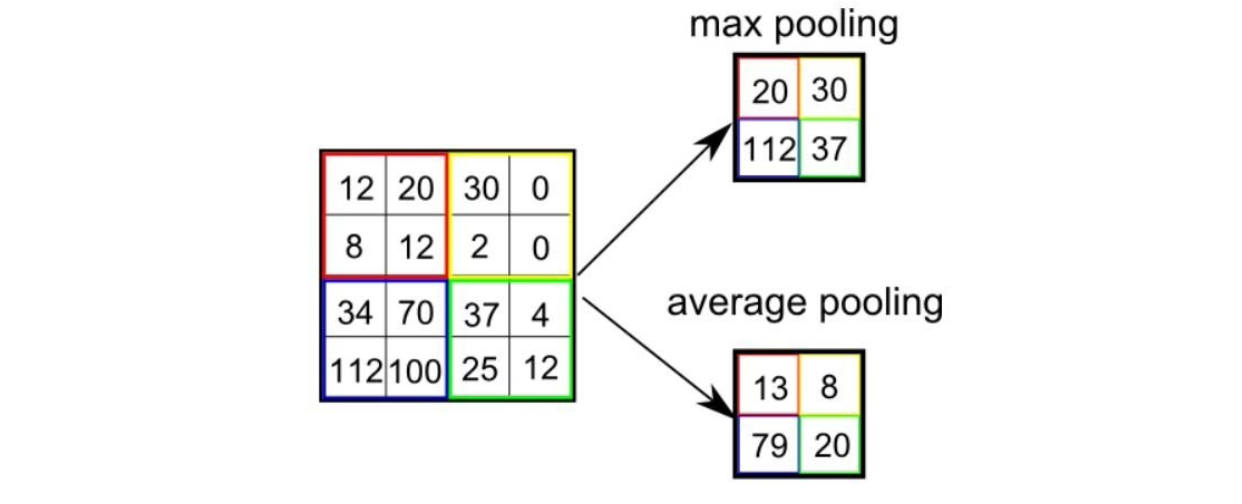이름 그대로 pooling은 local 값들을 하나의 어떤 값으로 대체하게 된다. Max pooling은 max operator를 사용해서 값들 중에서 가장 큰 값을 선택하게 된다. 반면 average pooling은 값들의 평균을 내어 그 반올림 값을 선택하게 된다.

Data Augmentation

Computer vision에서 이미지의 정보에 대해서 prior를 이해하는 방법 중 하나로 data augmentation이 있다. Image classification task를 한다고 했을 때, 이미지의 개수가 충분치 않을 수 있다. 이렇게 데이터셋이 적을 때 늘리는 효과를 내주는게 바로 data augmentation이다.
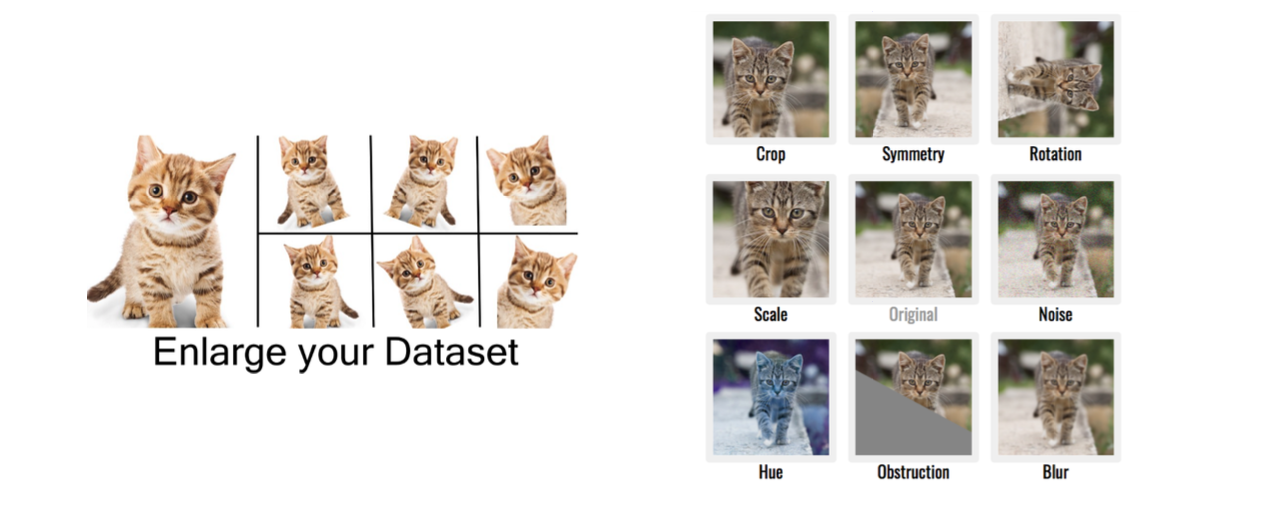이미지에 대해서 기울이거나 잘라내어 마치 다른 이미지인 것처럼 만들어 데이터셋을 늘리는 효과를 만들 수가 있다. 원래의 데이터에 대해서 (x,y)라고 했을 때 같은 label y에 대해서 x만 계속해서 바꿔주는 식이다.

이러한 data augmentation은 computer vision 외에도 natural language task에도 적용이 될 수 있다.
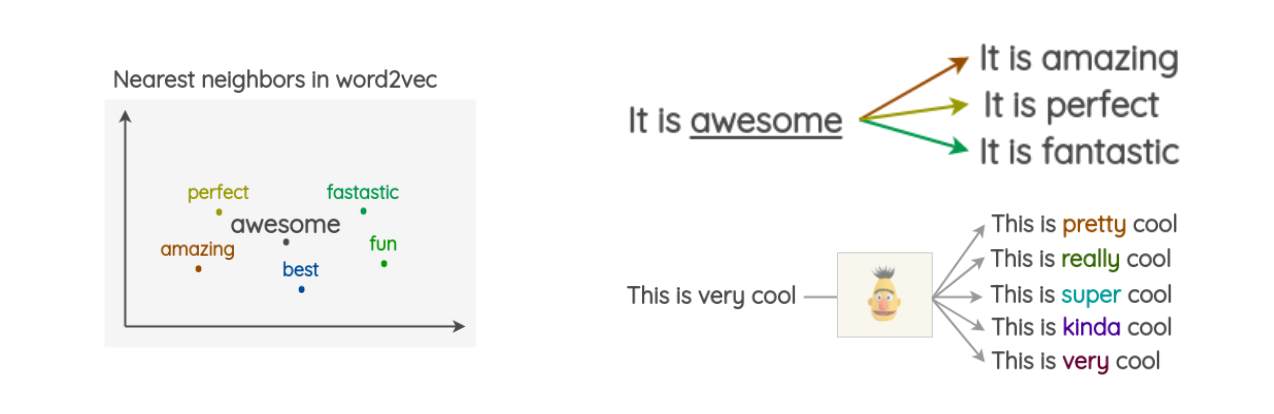하나의 문장이 주어졌을 때, 특정 단어를 같은 의미를 가지는 다른 단어로 대체할 수 있다. Very라는 단어도 pretty, really, super, kinda 등과 같이 대체할 수 있다.

Fair Comparison between Models

지금부터는 좋은 model을 선택하기 위해서 fair comparison에 대해서 알아보려고 한다.

No Free Lunch(Theorem)

만약 우리가 하려고 하는 일이나 데이터셋에 대해서 range를 정하지 않으면, 이에 대해서 generalization을 이야기할 때 그 의미가 다소 불분명하다. 다른 말로 model을 선택하는데 있어서 free lunch라는 것은 존재하지 않는다. 이게 무슨 소리일까? 일단 매우 구체적인 시나리오데 대해 정의하고 매우 완벽한 model을 만든다고 했을 때, 이 model은 내가 가정한 상황에 대해서만 한정적으로 완벽한 model이 되는 것이다. 만약 같은 model을 이용해서 여러 분야나 다른 시나리오에 적용하게 된다면 많은 overfitting이나 underfitting과 같은 여러 문제를 겪게 될 것이다. 즉, 이 세상에는 모든 일에 완벽하게 적용이 되는 유일한 model이나 학습 알고리즘이 존재하지 않는다는 것이다.

Generalization

Gerneralization을 이야기 할 때는 좀 더 신중해질 필요가 있다. 만약 일반적인 상황들에 대해서 general model을 build하고 싶다면 좋은 overfitting(특정 상황)과 generalization(일반적인 상황) 사이의 trade-off를 찾아야 한다. Parameter의 개수가 늘어나면 늘어날수록 training performance에 대해서는 좋아지게 되지만 testing performance에 대해서는 더 안좋아지게 된다. Overfitting이 일어나게 되면 적절한 model과 regularizer를 찾을 필요가 있다.

Ridge regression에서는 model parameter w에 대해서 $\lambda$가 regulization의 정도를 조절할 수 있었다. $\lambda$에 따라서 testing performance가 달라지게 된다. Overfitting 문제를 완화하기 위해서 $\lambda$는 어떻게 선택이 되어지게 될까? Test 데이터셋이 있다고 가정했을 때, training 데이터셋으로 model을 학습시키고 test 데이터셋으로 확인할 수 있다. 이때 test 데이터셋을 통해서 $\lambda$ 값을 찾을 수가 있다. 그렇지만 현실적으로 test 데이터셋으로부터 그 값을 찾기란 쉽지 않다.

Cross Validation

그래서 validation 데이터셋을 이용해서 값을 결정하려고 한다. Test 데이터셋에 대해서 hyper parameter을 찾기 위해서 cross validation 방법을 사용하면 된다. Cross validation은 4-fold cross valication으로도 불리는데, 이는 데이터셋을 4개로 분할하기 때문이다.
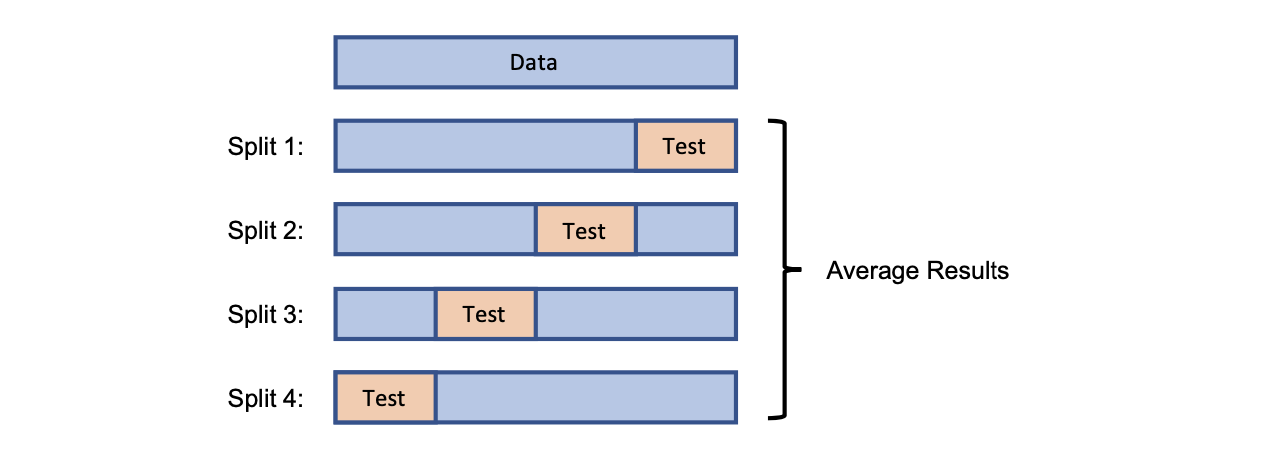이렇게 4개의 validation set이 생기면 각각에 대해서 3부분은 training 용으로, 나머지를 test 용으로 사용하여 test performance를 측정하면 된다. 그리고 마지막에 test performance를 이야기 할 때는 각각의 결과를 통해서 평균을 내어주면 된다. 이는 굉장히 그럴듯해 보이는 해결 방안이다. 사실 hyper parameter는 굉장히 많은데, 이렇게 4개로 분할해서 측정하게 될 때는 임의의 hyper parameter를 통해서 결과를 내기 때문에 처음 우리의 목적에는 부합하지 않는다. 우리는 적절한 hyper parameter를 찾고 싶다.

Hyper Parameter Selection: Nested Cross Validation

적절한 hyper parameter를 찾기 위해서 다음과 같이 nested cross validation을 할 것이다.
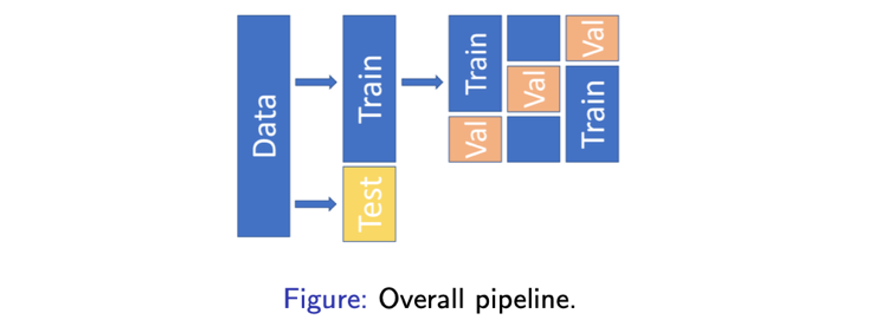먼저 데이터셋을 training과 test로 나눌 것이다. 그리고 training 데이터셋에 대해서만 validation performance를 최대로 하는 hyper parameter를 optimize하고자 cross validation 기법을 적용하려고 한다. 그리고 이를 통해서 이전에 만들어둔 test 데이터셋에 적용할 것이다. 이렇게 진행하는 것이 꽤 그럴듯한 hyper parameter optimization이다. 하지만 이는 다소 computational cost적인 측면에서는 heavy하다. 왜냐하면 optimal hyper parameter를 찾기 위한 cross validation이 많은 시간 수행되기 때문이다.

Hyper Parameter Selection: Train/Validation/Test

그래서 이를 단순화하고자 데이터셋을 train, validation, test용으로 나누는 것이다. 이는 데이터셋이 클 때 매우 간단한 해결책이다. 그러면 model을 training 데이터셋으로 학습을 시키고, validation 데이터셋을 통해서 hyper parameter를 찾고 이를 테스트 데이터셋에 적용시킬 수 있다. 이러한 방식이 딥러닝이나 여러 분야에 있어서 표준이 된다.

Optimal hyper parameter는 bayesian optimization과 같은 방식으로 찾을 수 있다. 우리는 training과 test 데이터셋에 대해서 bayesian optimization을 하게 된다. 이는 일종의 trial and error 방식이며, $\lambda_1$을 처음에 선택하고 이를 이용해서 학습을 진행하고 이를 validation 데이터셋으로 찾은 값으로 바꾸게 된다. Validation performance가 우리가 원하는 optimzation 결과이고, 이를 여러 $\lambda$에 대해서 진행한 뒤에 나온 값들을 기반으로 maximum validation performance에 대한 $\lambda$를 찾으면 된다. 그리고 이 값을 기반으로 test 데이터셋에 적용시켜 test performance를 측정하면 된다.