[선형대수] An Example of Gaussian Elimination

Gaussian Elimination

이제 Gaussian Elimination에 대해서 자세하게 알아볼 것이다. Ax = b 혹은 특수한 경우인 Ax = 0을 풀고 싶을 때, 어떻게 해야하는지 다음의 식을 가지고 알아볼 것이다.
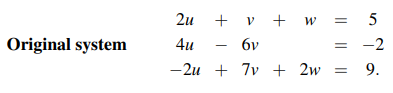우리는 위의 방정식들로부터 미지수인 u, v, w를 찾고 싶다. 그래서 우리가 할 행동은 첫번째 식을 가지고 나머지 식과 뺼셈 연산을 할 것이다. 이 연산의 목적은 미지수의 개수를 줄이기 위해서이고, 첫번째 식에 2를 곱해서 두번째 식과 뺄셈 연산을 하고, 첫번째 식에 (-1)을 곱해서 세번째 식과 뺄셈 연산을 할 것이다. 왜 2와 -1인가? 우리의 목표는 두번째 식과 세번째 식에서 미지수 u를 없애고 싶다. 그러면 다음과 같이 식이 변형된 것을 볼 수 있다.
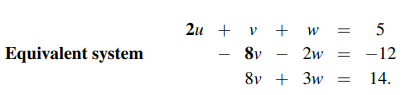여기서 첫번째 식의 u의 계수인 2를 첫번째 피벗(Pivot)이라고 한다. 피벗은 특정 계산을 수행하기 위한 임의의 알고리즘에 의해 먼저 선택된 행렬의 성분(항, 원소)이다. 이 피벗은 나중에 중요한 역할을 하게 될 것이다. 다시 돌아와서, 우리는 두번째 식을 가지고 세번째 식과 뺄셈 연산을 할 것이다. 두번째 식에 (-1)을 곱해서 세번째 식과 연산을 하면 세번째 식에서 v항을 지울 수가 있다. 그러면 다음과 같이 삼각형과 같은 형태로 미지수가 사라진 것을 볼 수 있다.
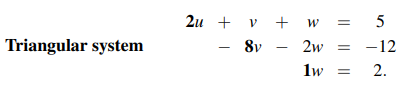최종적으로 두번째 식에서 v의 계수인 (-8)이 두번째 피벗이 되고, 세번째 식에서 w의 계수인 1이 세번째 피벗이 될 것이다. 이렇게 하면 결과적으로 어떻게 되었는가? 세번째 식에는 w만 남게 되어 w의 값이 2로 정해질 수 있게 되었다. 그러면 이제 이 정해진 w를 이용해서 두번째 식에 대입하면 v의 값이 정해지고, 이 값들을 다시 첫번째 식에 대입하면 u까지 구할 수 있게 된다. 이 과정은 후방 대입(Back Substitution)으로 소거법에서 값을 찾을 때 수행하게 된다. 그리고 위의 식이 삼각 구조를 이루기 때문에 Triangular System이라 한다.
이처럼 선형 방정식들이 주어졌을 때, 이것을 피벗을 중심으로 그 밑을 소거하여 Triangular System으로 만들고 Back Substitution을 이용해서 해를 구하는 과정을 Gaussian Elimination이라고 한다. 그리고 지금까지의 과정을 Matrix Notation을 사용해서 표현하면 다음과 같다. 그리고 앞으로는 미지수 없이 이런식으로 많이 사용이 될 것이다.

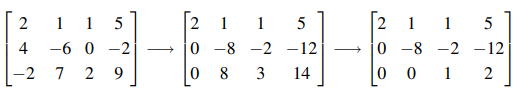
피벗(Pivot)이 0이 되는 경우

위는 정말 자연스럽게 해를 구하는 과정이 이루어졌다. 이는 3개의 식에서 3개의 피벗이 모두 0이 아니기에 가능했다. 즉, n개의 식과 미지수가 있을 때, n개의 피벗이 존재한다면, 해는 한개로 특정할 수 있다. 피벗이 0이 되는 경우는 두가지로 나눌 수 있다.

1. Nonsingular (Equation Exchange가 필요한 경우)
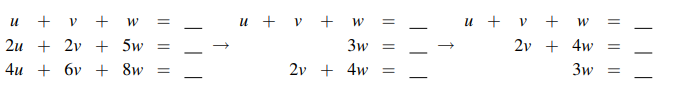   위의 경우는 뺄셈 연산 도중에 두번째 식의 피벗이 0이 되었을 경우이다. 이러한 경우에는 방정식 교환(Equation Exchange)를 이용해서 두번째 식과 세번째 식의 위치를 바꿔서 Traingular System을 만들어주면 해결이 가능하다. 물론 이렇게 식의 위치를 바꾸는 행동은 상관이 없다.

2. Singular (Triangular System을 만들 수 없는 경우)
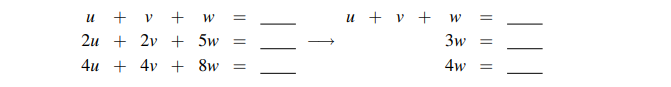   위아 같이 식의 위치를 바꿔도 안되는 경우가 있을 것이다. 이러한 경우에는 더이상 Gaussian Elimination을 진행할 수 없고, Singular case로 분류하면 된다. 즉, 해가 없을 수도 있고, 무수히 많을 수도 있다.