기하학적 접근
선형 방정식들의 기하학적인 접근은 방정식들 자체를 사용하는 행(Row) 접근법이 있고, 방정식들의 계수를 사용하는 열(Column) 접근법이 있다. 다음의 예시를 통해서 어떻게 기하학적으로 접근할 수 있는지 알아볼 것이다.
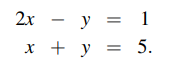
행(Row) 접근법
사실 이 방법은 굉장히 우리에게 친근할 것이다. 어릴적부터 이 방법으로 방정식들의 해를 구해 왔으며, 만약에 차원 수가 2라면 더더욱 빠르게 풀 수 있다. x축과 y축을 그려서 선형 그래프의 교점을 찾으면 되기 때문이다. 위의 식은 2차원으로 표현이 되며 직선으로 그릴 수 있다.
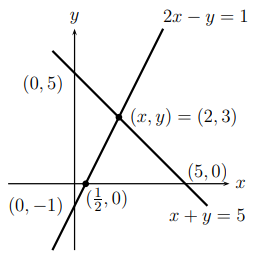우리는 두 직선이 교차하는 지점의 x값과 y값을 찾으면 된다. 그래고 이 값들이 방정식들의 해가 되는 것이며, 찾는 방법은 소거법(Elimination)을 이용하면 쉽게 찾을 수 있을 것이다.
열(Column) 접근법
이 방법은 앞으로 배우는 선형 대수에서 자주 볼 수 있으며, 벡터(Vector)를 이용하여 방정식을 새롭게 만들어 해를 구하는 것이다. 위의 2개의 방정식은 다음과 같이 하나의 벡터 방정식으로 바뀌는 것을 볼 수 있다. 우리는 이를 Column form이라고 말할 것이다. 그리고 여기서 각 방정식들의 계수를 새롭게 행렬로 바꾸어 세로로 적어 2개의 식을 1개로 바꾼 것이다. 우리는 이 식을 만족하는 x와 y를 찾으면 되는 것이다.
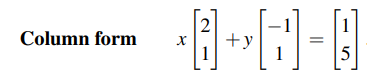
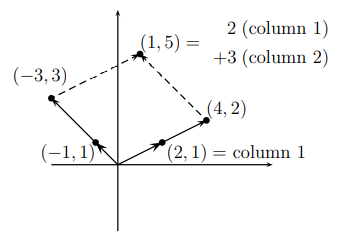
우리가 주목할 것은 이제 어떻게 우변의 벡터를 만드는 좌변의 벡터 식의 조합을 가지고 해를 찾을 수 있는 것인가이다. 위의 식을 보면, 좌변의 2개의 벡터를 이용해서 우변의 1개의 벡터를 표현하고 있다. 이처럼 벡터 여러개에 상수를 곱해서 만든 것을 선형 결합(Linear Combination)이라고 한다. 기하학적으로 풀고자 한다면, 아래 그래프에서 (2, 1)과 (-1, 1) 벡터를 이용해서 (1, 5) 벡터를 만들어야하는 셈이다. 이는 어떠한 상수갑들을 곱해서 벡터의 상수배를 만들어 구하면 되고, 여기서 곱해진 상수값들이 벡터 형식의 방정식에서의 해가 된다.
일반화
그러면 이제 조금 더 복잡한 경우를 생각해서, n = 3일 때는 어떤지 볼 것이다. 2차원이 직선이라면, 3차원은 평면이 되는 것이고, 만약 이를 그림을 그려 해결하고자 한다면 난해할 수 있다. 아래 그림을 보면 저것을 그린다고 어떠한 해답이 나오지는 않는다. 정말 그림에 소질이 있고, 그림을 통해서 값이 도출이 된다면 상관은 없을 것이다. 하지만, 일반적으로 쉽지는 않다.
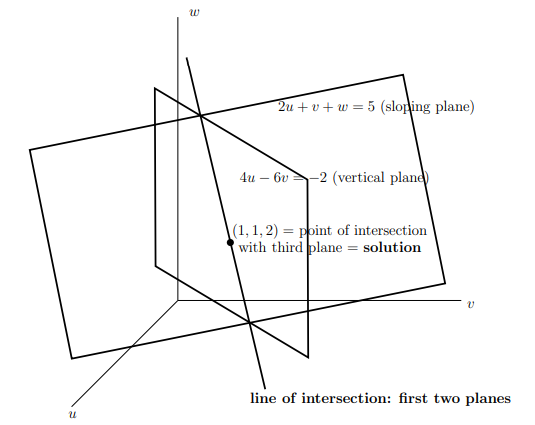아래의 식을 예를 들어보자.
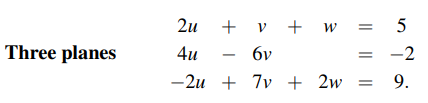이를 행 접근법을 이용해서 풀고자 한다면 똑같이 소거법과 후방 대입을 이용해서 미지수를 하나씩 찾아가면 된다. 하지만 n이 무수히 많아진다면, 하나씩 값을 찾아내서 원래 방정식들에 대입해서 다른 해를 구해가는 것은 효율적이지 못하다. 그래서 이를 열 접근법을 통해서 풀어볼 것이다. 위의 식을 Column form으로 바꾸면 다음과 같다.
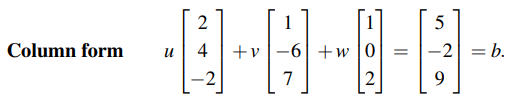그리고 여기서 b = (5, -2, 9)이다. 사실 지금까지 벡터를 괄호를 이용해서 적었는데, 이는 어떻게 적어도 괜찮다. 화살표를 이용해도 되고, 대괄호를 이용해도 되는 것이다. 여기서 핵심은 벡터를 어떻게 표현하느냐가 아니라, 벡터의 덧셈(Vector Addition)과 스칼라 곱셈(Multiplication by Scalar)의 개념을 알고가는 것이다.
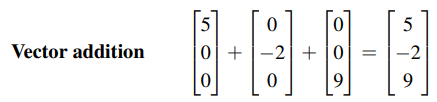우변의 b는 사실 3개의 방향을 가진 벡터의 합으로 표현이 되었다. 위와 같이 같은 행의 값들을 더해서 새로운 벡터를 만들어 낼 수 있다.
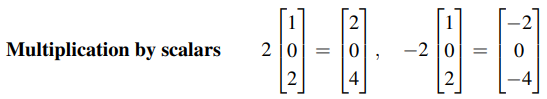어떤 벡터의 상수를 곱하게 되었을 때, 해당 벡터의 모든 값들이 상수배를 가질 수 있다. 물론 음수를 곱하게 된다면, 부호가 바뀌게 될 것이다. 그래서 다시 Column form을 보게 되면, 이제는 같은 식이어도 다르게 보일 것이다. 우리가 찾을 해인 u, v, w는 사실 벡터의 특정 상수배이고, 이들의 덧셈으로 우변의 벡터가 만들어지는 것이다. 그리고 이는 선형 결합 형태인 것을 알 수 있다.
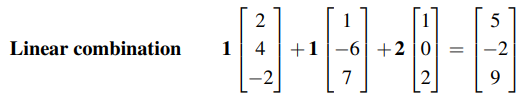사실 u, v, w를 직접 구하는 방법은 앞으로 볼 것이며, 지금은 저러한 방식으로 식을 보는 관점을 바꿔 문제를 해결할 수 있다는 것을 알아야 한다.
부정방정식(Singular Case)
우리가 여러 방정식을 통해서 하나의 해를 찾겠다는 것은 굉장히 일반적인 경우에 해당한다. 가령 계수의 조합이 특이하게 되었을 경우, 우리는 하나의 해를 단정짓기 어려워진다. 그리고 이러한 부정방정식이라 하고, singular case이다. 뒤에서 정칙 행렬(Singular Matrix)에 대해서는 자세하게 알아볼 것이다. 이 케이스는 해가 아예 없거나, 해가 무수히 많은 경우가 해당된다. 가장 쉽게 생각할 수 있는 것은 2차원에서 직선이 평행한 경우가 있을 것이다.
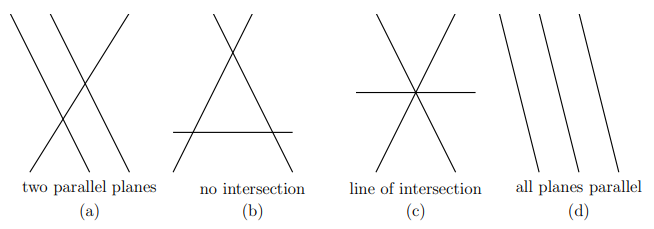위에는 다양한 singular case를 보여준 것이고, 여러 plane들을 위에서 내려다본 것이다. 그래서 (a), (b), (d)는 해가 없는 경우이고, (c)는 해가 무수히 많은 경우에 해당한다. 아무래도 가장 어려운 경우는 (b)일 것이다. 교차하는 직선이 평면들마다 존재하지만, 이 직선들이 평행하기 때문이다. 다음은 부정방정식의 한가지 예제이다.
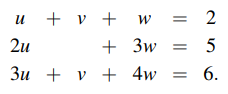그리고 이를 Column form으로 바꾸어 벡터의 관점으로 볼 것이다.
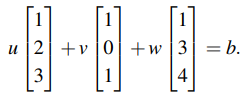
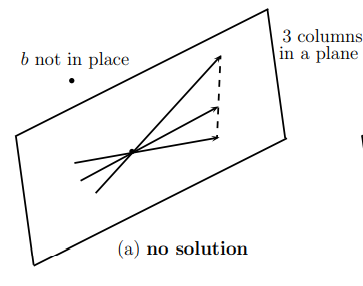
세 벡터가 한 공간에 있는 경우(No Solution)
다음과 같이 3개의 벡터가 이루는 공간에 b가 놓여있지 않으면, 해는 없게 된다.
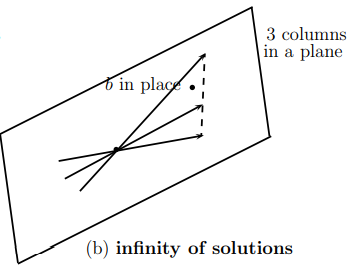
세 벡터가 이루는 공간에 b가 있는 경우(Infinity Solution)
다음과 같이 3개의 벡터가 이루는 공간에 b가 놓여 있으면, 해는 무수히 많게 된다.
우리는 어떻게 3개의 벡터가 하나의 공간 위에 있다는 것을 알 수 있을까? 한가지 답으로는 특정 상수배를 한 뒤에 이를 더했을 때 0이 되는 벡터의 조합이 있는지이다. u = 3, v = 1, w = -2인 경우가 이에 해당한다. 3(1, 2, 3) = 1(1, 0 ,1) + (-2)(1, 3, 4)라는 식이 가능하다(이는 다음 내용에서 더 정확히 다룰 것이다). 이 경우가 만족한다면, 3개의 벡터는 한 공간에 있게 되는 것이다. 그리고는 b가 동일 평면 상에 존재하는지를 따져서 해가 무수히 많은지, 아니면 아예 없는지 찾으면 된다. 사실 해가 1개로 단정되지 못한 경우인 것을 알면 b가 어떤지 구할 필요가 없을 때가 많다.
