Matrix Notation
이제 방정식을 그대로 사용하지 않고 행렬의 형태로 계수들만 사용해서 표현할 것이다. 우리는 주어진 방정식을 벡터들의 연산인 Column Form으로도 바꿨었는데, 이를 더 효율적으로 보기 좋게 바꾸게 되면 행렬식으로 바꿀 수 있다.
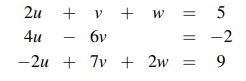위의 예시에서 우리가 확인할 수 있는 정보로는 좌변에 9개의 계수(Coefficient), 3개의 미지수(Unknowns)가 있고 3개의 우변항이 존재한다. 우리는 이 정보들을 따로 행렬로 만들어 전체 식을 행렬 형태로 바꾸고 싶다.
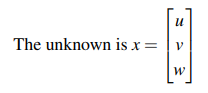위처럼 미지수들은 하나의 x 벡터로 표기하는 것이 자연스러운 표기법이다. 우리가 찾아야 할 해들만을 모아서 x 벡터로 만들었다.
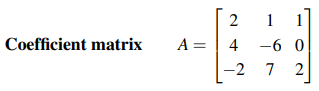그리고 9개의 계수들로 Coefficient Matrix A를 만들 수 있다. 아무래도 A는 정사각 행렬일 수 밖에 없다. 왜냐하면, 방정식의 수와 미지수의 수가 n으로 동일하기 때문이다.
그리고 다음과 같이 행렬의 기본 연산으로 덧셈(Addition)과 덧셈(Multiplication)이 가능하다는 것은 이미 알고 있는 사실이다. 기본적인 내용이지만, 이 내용에 기반하여 행렬의 값을 바꿀 수가 있는 것이다.
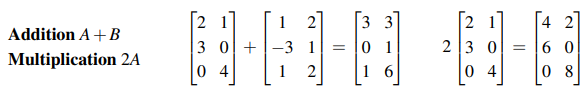
Multiplicaton of a Matrix and a Vector
그래서 우리는 결국 3개의 미지수가 존재하는 3개의 방정식을 Ax = b의 형태로 바꾸고 싶다. 그래서 위에서 정의한 대로 같은 속성을 가진 것들을 행렬과 벡터로 만들어 다음과 같은 형태로 만들 수 있다. 번거롭겠지만, 곱셈과 덧셈을 하나하나 해보면 결국 처음 등장했던 원래의 3개의 방정식과 같은 식들이 만들어지게 된다.
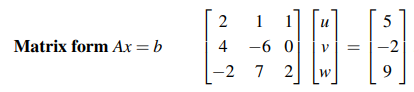A에서 첫번째 행과 x를 따로 떼어내서 보면 다음과 같이 우변의 첫번째 항인 5를 만들게 된다.
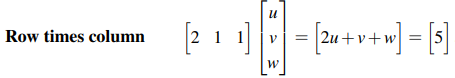이러한 방식으로 A의 두번째 행과 세번째 행도 계산이 가능하다. 지금까지의 방식은 A의 행을 이용하여 계산을 진행하는 방법이고, A의 열을 이용해서도 계산을 진행할 수 있다. 두 방법 모두 알고 있으면 좋지만, 행보다는 열의 관점으로 계산할 줄 아는 것이 더 중요하다. 다음은 하나의 예시인데, 예시를 통해서 어떠한 차이가 있는지 알 수 있을 것이다.
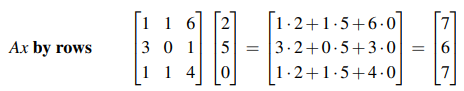위 방법은 A의 행을 x와 곱해나가는 방식이다.
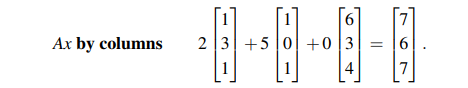위 방법은 A의 열을 x의 원소 하나씩 곱해나가는 방식이다. 물론 위 두개의 방법은 결과가 똑같다. 단지 이렇게도 할 수 있고, 저렇게도 할 수 있다는 것을 알아둬야 한다.
Elementary Matrix
우리는 Gaussian Elimination 에서 한 번의 Elimination 단계를 행렬로 표현이 가능하다. 이를 우리는 기본 행렬(Elementary Matrix)이라고 한다. 이 기본 행렬들을 잘 정리해둬야 Gaussian Elimination 전체의 과정이 쉽게 정해질 수 있다. 우리는 주어진 방정식을 Ax = b로 바꾸었을 때, 양변에 기본 행렬들을 곱해줌으로써 Elimination 단계를 진행할 수 있다.
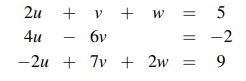다시 그러면 처음 예시로 돌아가서 어떻게 기본 행렬을 만들 수 있는지 알아보도록 할 것이다. 우리는 첫번째 식에 2를 곱해서 두번째 식과 뺄셈 연산을 진행했다. 그렇게 해서 두번째 식의 미지수 u를 없앴는데, 이 과정을 다음과 같이 대각선의 원소가 1인 행렬에 두번째 행의 첫번째 열에 해당하는 원소에 (-2)를 기입함으로써 만들 수 있다.
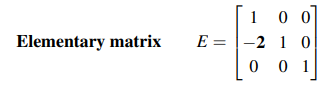이 기본 행렬을 우변의 b와 곱했을 때 똑같은 결과가 얻어지는 것을 확인할 수 있다.
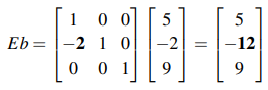여기서 원소 5와 9는 각각 (1, 0, 0)과 (0, 0, 1)을 곱했기 때문에 값이 바뀌지 않았다.
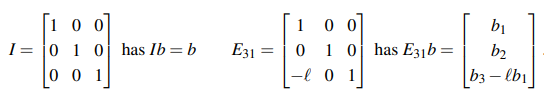우리는 기본 행렬을 만들기 위해서 단위 행렬(Identity Matrix)를 베이스로 사용할 것이다. Eij이라고 한다면 j행에 l을 곱해서 i행에서 뺼셈 연산을 진행했다고 생각하면 될 것이다. 이렇게 기본 행렬들을 찾아서 E(Ax) = Eb와 같이 양번에 곱해주면 새로운 System 이 만들어지고, 이렇게 단위 행렬을 한번 곱함으로써 Gaussian Elimination을 한 단계 진행했음을 알 수 있다. 그리고 Ax = b와 E(Ax) = Eb는 정확하게 같은 해를 가지고 있다.
Matrix Multiplication
우리는 원래 행렬인 A와 기본 행렬인 E를 알고 있고, 이를 곱하게 된다면 다음과 같이 될 것이다. 원래 행렬과 기본 행렬의 곱셈은 Gaussian Elimination 과정에 있어 가장 자주 등장하는 행렬 곱셈이다.
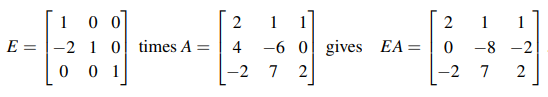여기서 하나 짚고갈 내용으로, 위에서 기본 행렬을 곱한다고 했을 때, E(Ax) = Eb라고 적었다. 사실 행렬은 행과 열의 변하지 않는 성질의 곱셈이기 때문에 괄호가 크게 의미가 없다. 그래서 E(Ax)라고 적어도 되고 (EA)x라고 적어도 된다. 일반적으로는 괄호는 의미가 없기 때문에 역행렬을 표시하는 것이 아니면 굳이 적지 않고 EAx라고 바로 적는다.
지금부터 행렬의 곱셈에 있어 몇가지 성질과 같은 것들을 확인해볼 것이다. 만약에 행렬 B가 오직 한개의 열만 가지고 있는 것이라면, 행렬 A와 행렬 B의 곱인 AB는 행렬과 벡터의 곱인 Ax와 일치하게 된다. 하지만 B가 여러개의 열을 가지고 있다면 다음과 같이 표현할 수 있을 것이다.
그리고 A와 B의 곱에서 특정한 원소를 구하고 싶으면 다음과 같이 찾으면 된다. 예시로는 AB의 3행 2열의 원소를 표현한 것이고, 이는 A의 3행과 B의 2열의 내적을 통해서 얻을 수 있다.
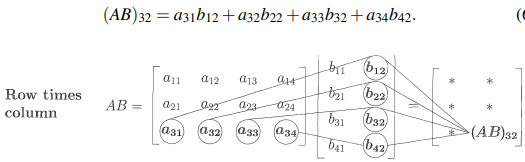다음은 행렬의 곱셈을 3가지 형태로 표현한 것이다.
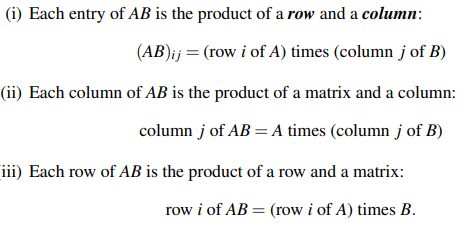단순히 보면 어려워보일 수 있지만, 너무나도 당연한 이야기를 적어놓은 것이다. (i)는 바로 위에서 설명한 AB의 특정 원소에 대한 이야기이다. (ii)와 (iii)은 AB의 행과 열에 대한 이야기로, AB의 j번째 열은 A와 B의 j번째 열을 곱해서 얻을 수 있고, AB의 i번째 행은 A의 i번째 행과 B를 곱해서 얻을 수 있다.
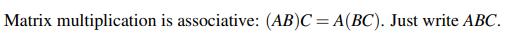위의 내용도 사실 이미 다뤘던 내용으로 행렬의 곱셈도 곱셈의 성질을 그대로 가지고 있어 어느 것을 먼저 곱하든지 간에 결과는 동일하게 된다.
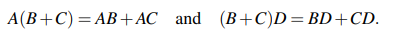그리고 분배해서 곱하는 것도 곱셈의 성질과 같아 행렬에서도 가능하다.
하지만 곱셈의 성질 중 하나인 교환 법칙은 행렬에서는 성립하지 않는다. 행렬에서는 행과 열의 2차원 데이터를 다루기 때문에, 곱셈에서의 차원 수도 맞춰야 하기에 바꿔서는 계산이 불가능하다.
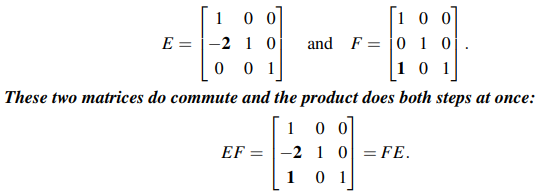위의 성질은 기본 행렬을 여러번 곱할 때 편리할 것이다. Gaussian Elimination을 한 단계만으로 끝내는 경우는 드물 것이다. 이럴 경우에 기본 행렬이 무수히 많이 생길 것인데, 이를 위와 같이 하나의 행렬로 표현할 수 있다면 하나의 행렬만으로도 Gaussian Elimination 전체 과정을 설명할 수 있다.
