두 벡터 x와 y가 서로 orthogonal 할 때, 우리는 이 두 벡터가 서로 orthogonal 함을 이제는 당연하게 받아들일 수 있다. 이번 단원에서는 두 벡터가 주어졌을 때, 내적이 0이 아니고 orthogonal 하지 않은 경우에 대해서 다뤄볼 것이다. 다음의 상황을 가정하고 시작해보자.
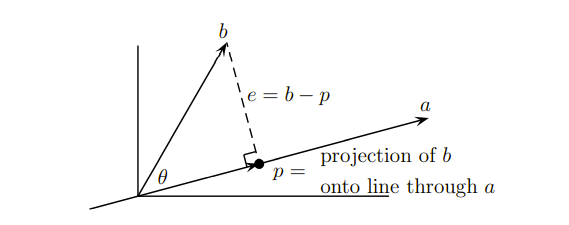위의 상황은 벡터 b가 벡터 a 위로 정사영 한 것으로, 이때의 점은 a위에 놓인 p가 된다.
우리가 ax = b가 해를 가지기 위해서는 b가 C(a)에 있어야 한다는 것을 알고 있다. 그렇다면 반대로 해가 없다는 것은 b는 C(a)에 없다는 것이 된다. 우리는 이제 해가 없다고 하면 해가 없다고 하고 넘어갈 것이 아니라, 최대한으로 근접한 해를 찾으려고 할 것이다. 그리고 이것을 least squre solution이라고 하고 다음과 같이 x위에 꼬깔 모자를 쓴 것 같다 해서 'x hat'이라고 읽을 것이다.
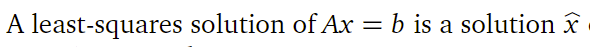
실제로 b를 a의 방향으로 연장한 직선에 projection 시킨 벡터 p가 b와의 차이가 최소가 되는 벡터일 것이다. 우리는 이런 p를 찾고 싶고, 이는 몇가지의 개념만 알면 쉽게 알아낼 수 있다.
Inner products and cosines
다음과 같이 벡터 a와 b가 x축으로부터 α, β의 각도를 가지고 있다고 해보자.
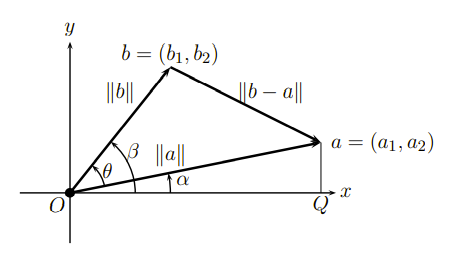가장 기본적인 sine과 cosine을 a 벡터의 x 값과 y 값을 통해서 다음과 같이 구할 수 있다.
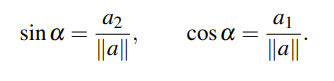b 벡터도 똑같이 구할 수 있다. 그럼 이 상황에서 θ = β - α라고 한다면, cosθ는 다음과 같이 cosine formula를 통해서 구할 수 있다.
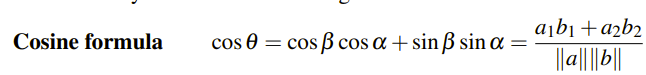그리고 위의 식에서 분자는 두 벡터의 내적의 식과 같아서 다음과 같이 식을 표현할 수도 있다.
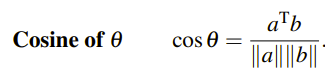
Projection onto a Line
만약 θ가 주어지지 않으면, cosθ는 사용할 수없다. 그래서 cosθ를 벡터화 시킨 것이다. 이제 cosine을 벡터의 내적으로 표현할 수 있다는 것을 알게 되었으니, 이를 이용해서 벡터 p를 찾아볼 것이다.
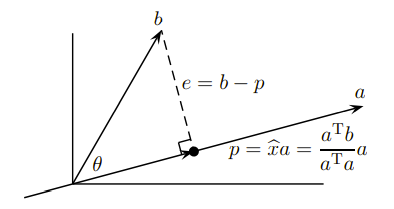우리는 두 벡터가 직교할 때 내적이 0이라는 사실을 알고 있다. 이를 그대로 위에서 주어진 벡터들로 표현하면 다음과 같고, 여기서 우리는 least square solution을 찾을 수 있다.
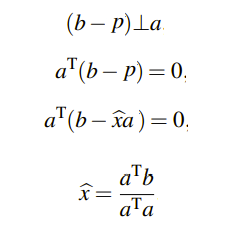우리가 최종적으로 찾고 싶은 것은 p 이기 때문에 위에서 찾은 least square solution을 대입하면, 다음과 같이 직선위에 projection한 점 p가 벡터 식으로 표현이 된다.
Projection Matrix of Rank 1
이전에 projection matrix를 배웠는데, 이때는 xy 평면 위에서 y = (cosθ)x로 projection 시키는 행렬이었다. 그렇지만 이번에는 n차원 공간에서 벡터 a의 방향으로 연장시킨 직선으로 projection시키는 행렬을 구할 것이다.
임의의 벡터 b를 a의 방향으로 연장시킨 직선 위로 projection 시킨 벡터를 p라고 하면, 우리가 구할 projection matrix P는 p = Pb를 만족시키는 P이다.
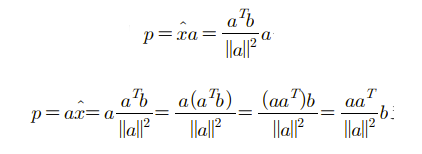위의 식을 통해서 우리는 projection matrix인 P만을 따로 구할 수 있다.
분모를 길이의 제곱을 써도 상관이 없고, 내적으로 적어도 상관이 없다. 예제를 통해서 간단하게 계산해보자.
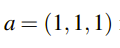a라는 벡터가 위와 같이 주어졌을 때, projection matrix P를 구하면 다음과 같다.
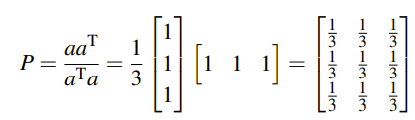이 행렬은 다음과 같이 2가지 성질을 만족한다.
1번은 P 자체로 만족하는 성질이고, 2는 계산해도 되지만, 의미적으로 projection한 결과는 이미 원하는 위치에 있기 때문에 몇번을 projection 해도 위치는 변하지 않는다.
