이전 내용에서는 ax = b인 미지수가 1개인 경우에 대해서만 알아보았다. 이번에는 이를 일반화시켜 식이 m개이고, 미지수가 n개인 m by n 행렬인 Ax = b인 경우에 대해서 알아볼 것이다. 이때, A의 열들이 linearly independent하다고 가정할 것이기에 이는 full rank를 가지고 있다. Linearly dependent한 경우는 나중에 알아보기로 한다.
Least Squares Problems with Several Variables
Ax = b는 해를 가지거나 가지지 않는다. b가 column space C(A)에 없다면, 해가 없을 것이다.
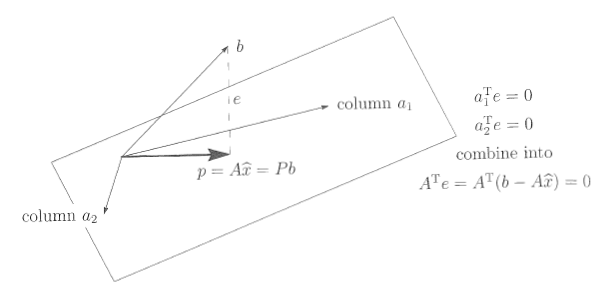
이때 위와 같이 least sqaure solution을 사용해서 b를 C(A)에 projection 시킨 벡터 p로 나타낼 것이다. p는 C(A) 위에 있고, C(A)에서 b에 가장 가까운 벡터가 될 것이다. 이때 오차 e는 벡터 b와 p의 거리로, C(A)와는 수직이 된다. Column space와 left null space가 orthogonal하기 때문에 e는 left null space에 있게 될 것이다. 그렇기 때문에 다음과 같은 식이 성립이 된다.
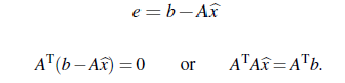우리는 이 식으로 부터 least square solution을 구할 것이다.
그러기 위해서는 A의 열들이 lienarly independent해야 한다.
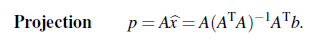앞서 구한 least square solution을 이용해서 projection p를 구할 수 있다. 예시를 통해서 보자.
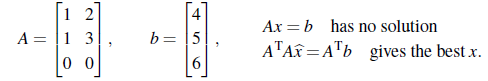A의 열에 모두 0이 있기 때문에, C(A)는 3차원 공간 상의 xy평면이 될 것이다. 위를 통해서 projection p를 구하면 다음과 같다.
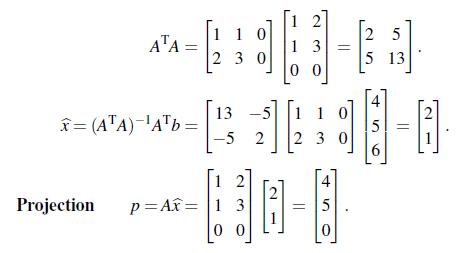가장 무난한 경우를 예시로 살펴보았으며, 다음으로는 몇가지 극단적인 경우를 살펴볼 것이다.
- b가 column space에 있는 경우: 그러면 다음과 같이 p는 b자체가 될 것이다.
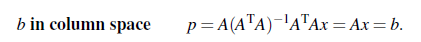
- b가 left null space에 있는 경우: 이 경우는 C(A)와 orthogonal한 공간에 있는 것이므로, p는 projection 하게 되면 0이 될 것이다.
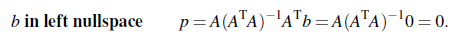
- A가 square하고 invertible한 경우: 그러면 A의 columnn space가 전체 공간에 해당하게 될 것이다. 그러면 모든 벡터 b는 projection하게 되면 자기 자신이 되므로, p와 b는 같게 될 것이다.
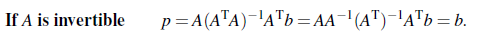
The Cross-Product Matrix
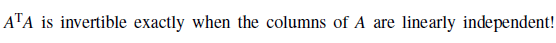이 문장을 다시 보자. Invertible의 성립을 확인을 해볼 것인데, symmetric은 당연히 성립하기에 넘어갈 것이다.
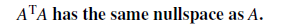그러기 위해서 위에 해당하는 명제에 대해서 증명을 할 것이다.
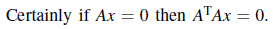당연한 사실이기 때문이기에, 이를 증명할 것이고 우변이 0이기 때문에 다음과 같이 쉽게 가능하다.
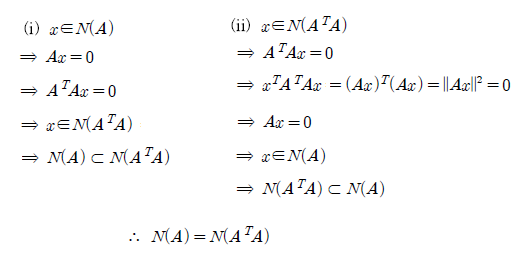결과적으로, 2개의 null space가 동일하게 된다. 그래서 A가 independent columns들을 가지게 되면, A와 A를 내적한 행렬도 자연스럽게 independent columns를 가지게 된다.
Projection Matrices
위에서는 임의의 벡터 p가 C(A)에 projection 되었을 때의 벡터 혹은 점 p를 구했지만, 이번에는 projection을 시키는 행렬 P의 대해서 알아볼 것이다.
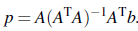그래서 b와 가장 가까운 p를 구하는 법을 알아봤었다. 그리고 이전에 p = Pb라고 해서 b를 projection 시키는 행렬 P에 대해서도 알아봤었다. 이 2개의 관계식은 사실 똑같은 형태를 취하고 있다.
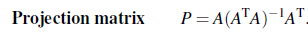그래서 P는 자연스럽게 b부분을 제외한 부분이 된다. 그리고 P는 다음과 같은 성질을 가지고 있다.
이는 직접 대입을 해보면 성립이 될 것이고, 반대의 경우도 생각해보자.
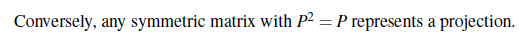제곱을 취하거나, 전치시켰을 때 자기 자신이 되는 행렬이 왜 projection 행렬이 되는 것일까? 다음과 같이 증명해볼 수 있다.
이 증명에서의 핵심은 b - Pb가 C(P)에 수직이 되는지이다. 다음의 예를 살펴보자.
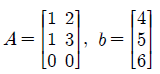Ax = b가 해가 없고, C(A)가 xy 평면임을 쉽게 알 수 있다. 따라서 b를 C(A)에 projection 시키면 p = (4, 5, 0)이 될 것이다. 정말 그렇게 되는지 위에서 알게 된 식을 통해서 확인해보자.
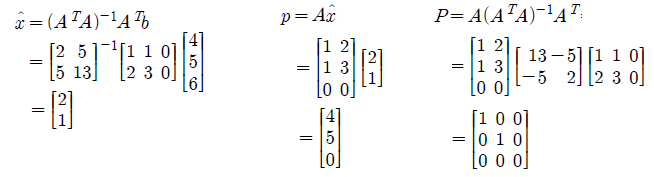Least square solution x, projected vector or point p, projection matrix P를 구할 수 있고, 예상했던 것과 같은 결과를 냈다.
Least-Squares Fitting of Data
지금까지 배운 least square를 이용해서 추세선을 그리는 방법을 알아볼 것이다. 어떤 실험을 통해서 n개의 (t, b) 데이터를 얻었다고 가정해보자. 그리고, t1 < t2 < ... < tn으로 값의 차이가 있다고 생각할 것이다. 우리는 이제 이 좌표들을 이용해서 좌표 평면에 오차가 가장 적도록 추세선 b = C + Dt를 그려볼 것이고, 여기서 C와 D는 어떤 상수이다.
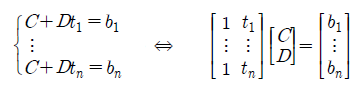직선의 방정식을을 Ax = b의 matrix form으로 바꿀 수 있고, 이 식은 미지수의 개수보다 방정식의 개수가 많아 해가 없다. 그래서 다음과 같이 best solution을 구해야 하고, 이 해는 squared error를 최소화하게 된다.
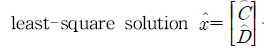
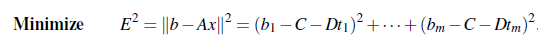예를 보자. 어떤 실험을 통해서 다음과 같은 데이터를 얻었다.
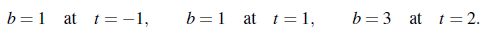이 데이터들을 이용해서 다음과 같이 행렬식을 나타낼 수 있다.
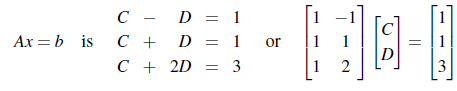
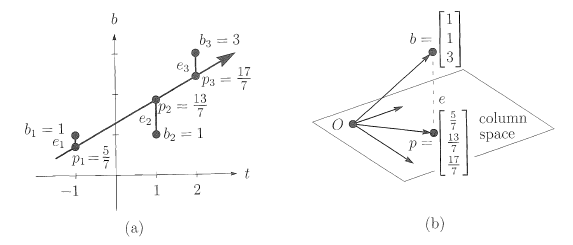만약 Ax = b의 해가 존재한다면, error는 없을 것이다. 하지만, 위의 데이터들이 직선을 만들 수 없어서 해를 구할 수 없다. 그래서 다음과 least square solution을 통해서 C와 D를 구할 수 있다.
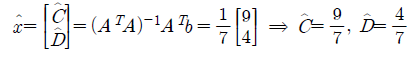따라서 9/7 + (4/7)t가 오차를 최소화 시키는 추세선이 되는 것이다.
