지금부터는 n차원의 벡터 v를 열벡터로 간주할 것이다. 그래서 그냥 v를 사용한다면, column인 것으로 생각하면 되고 여기에 transpose 기호인 T를 붙인다면, 행벡터로 간주하면 된다. 그리고 우리는 같은 공간 안에서 벡터를 표현하고 싶을 때, basis의 linear combination으로 표현하면 되는 것도 알고 있다. 여기서 linear combination은 basis인 벡터와 어떠한 상수의 곱으로 이루어지는 것도 알고 있을 것이다. Basis가 주어지는 상황이나 그렇지 않더라도 앞에서 공간의 특성에 따라 basis를 찾는 방법을 배워서 알고 있을 것이다. 그렇다면 상수배를 하기 위한 c값들은 어떻게 결정해야 하는 것일까? 만약에 basis들이 수직이라면 c를 구하는 것은 쉽다.
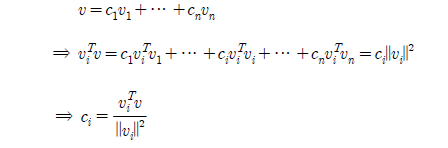위와 같이 구하고 싶은 상수와 곱해지는 basis를 모든 basis와 곱하면, 나머지 항은 수직이기 때문에 0이 될 것이다. 그러면 상수값들을 쉽게 구할 수 있다. 하지만 일반적으로 basis들이 전부 수직이라고 생각하기는 어렵다. 그래서 지금부터는 수직에 대해서 좀 더 다양한 이야기를 하고 최종적으로는 basis들을 서로 수직하게 바꾸는 일종의 작업을 해줄 것이다. 또한 linear equation의 해가 없는 경우에 이전에는 그냥 해가 없다면 넘어가는 식이었지만, 이제부터는 그래도 해에 근접하여 근사값을 구하는 방법도 알아볼 것이다.
기본 개념이겠지만, 몇개만 짚고 넘어갈 내용이 있다. 우선 length라고 하는 벡터의 길이를 구할 때 각각의 원소를 제곱해서 루트를 씌워주는 것은 알 것이다. 이는 3차원에서도 똑같이 해당하는 이야기이다.
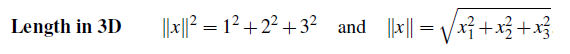그런데 이를 좀 더 확장하면 벡터의 길이의 제곱은 곧 벡터의 내적과 동일하게 취급할 수 있다.
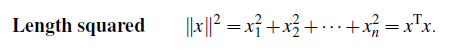다음의 예시를 통해서 바로 확인이 가능하다.
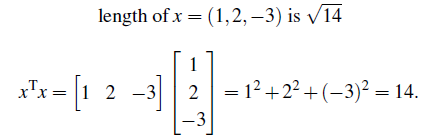
Orthogonal Vectors
두 벡터 x와 y가 주어졌을 때, 이 두 벡터가 수직한지 어떻게 알 수 있을까? 두 벡터 사이의 각도가 90도를 이루게 된다면, 이 두 벡터를 직교 벡터(Orthogonal vector)라 한다. 이때 벡터는 임의의 모든 n차원에 대해서 해당이 된다. 90도를 이룬다는 것은 다른 말로 표현하면 두 벡터가 직각 삼각형을 이루면 된다.
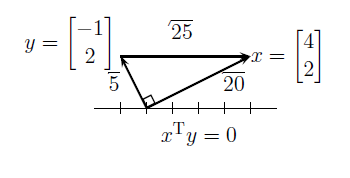두 벡터가 이루는 각도가 직각이고, 이는 피타고라스에 의해 정의된 직각 삼각형이다. 2차원에서는 위와 같이 표현하면 되는데, 이를 n차원으로 확대하면 어떻게 되겠는가? 직접 그리는데 어려움이 있을 수는 있으나, 이론적으로는 n차원의 두 벡터가 직교인지 확인하기 위해서는 내적을 통해서 확인하면 된다. 내적을 했을 때 값이 0이 되면 두 벡터는 서로 orthogonal 한 것이다.
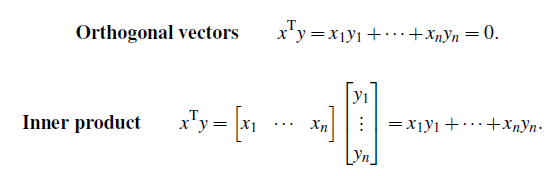우리가 원래 배운 내적의 식은 길이의 곱에 cosine 값을 곱해서 만들어진다. cosine은 90도일 경우에는 값이 0이 되기 때문에, 두 벡터가 orthogonal 할 경우 그 값이 0이 나오는 것이다.
벡터들이 서로 orthogonal하면, 이 벡터들은 linearly independent하다. 증명은 다음과 같다.
증명은 간단하기에 읽어보면 되지만, 간단하게 설명을 해보겠다. Linearly independent하다는 것은, 벡터들을 linear combination 했을 경우 오직 하나의 c값들만 나와야만 하는 것이다. 직교라는 조건이 얼마나 강한 조건인지 살펴보면 위와 같이 하나의 c를 구하기 위해서 linear combination으로 만들어진 임의의 벡터와 하나의 벡터를 내적했을 때, 나머지 벡터항들은 orthogonal하기 때문에 0으로 날라가고 하나의 항만 남는다. 이때 같은 벡터의 내적이 남게 되는데, 같은 벡터의 내적은 0이 되지 않기 때문에 해당하는 상수 값이 0이 되어야 한다. 이를 일반화시켜 나머지 벡터와 상수들의 경우에 전부 대입해보면, 모든 c의 값은 0이 되고, 유일한 경우만 존재하게 된다. 그렇기 때문에 orthogonal 하다는 조건이 있으면, independence는 보장이 된다.
그리고 orthogonal한 벡터들의 길이가 1인 경우에는 orthonormal하다고 이야기 할 것이다. 이 벡터들을 보통 unit vector라고 많이 하고 자주 쓰이는 것으로는 x축을 (1, 0), y축을 (0, 1)의 단위 벡터로 사용한다.
Orthogonal Subspaces
벡터뿐만 아니라 공간에 대해서도 orthogonal이란 말을 사용할 수 있다. 벡터의 orthogonality를 생각했을 때 이를 공간으로 확장시킨다면, 두 공간이 orthogonal하다는 말은 공간 내에 있는 어떠한 벡터를 잡아도 다른 공간과 orthogonal할 것이다. 그래서 하나의 공간 내에서 모든 벡터가 다른 공간 내의 모든 벡터들과 직교하면 이는 orthogonal 한 것이다.
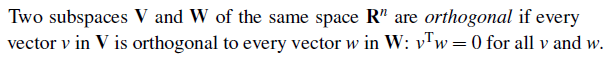정의를 통해서 정확히 알아보면, 두 부분 공간 V와 W가 orthogonal 하다는 것은 V의 모든 벡터가 W의 모든 벡터와 orthogonal하면 된다는 것이다. 즉, 벡터간의 내적이 0이 되면 된다. 그래서 보통은 V와 W의 basis를 가지고 orthogonal 한지만 확인하면 된다. 다른 벡터들은 basis의 linear combination으로 가능하기 때문이다.
우리가 지금까지 본 부분 공간들 중에서 orthogonal한 공간들이 존재한다. 첫번째로 살펴 볼 공간들은 null space와 row space이다. 이 두 공간은 m by n 행렬 A라고 했을 때, n차원의 부분 공간이 된다. 그러면 이제 왜 이 두 공간들이 orthogonal인지 알아볼 것이다.
x 벡터를 null space에 있다고 가정하자. 그러면 Ax = 0이고, 이는 다음과 같이 생각할 수 있다.
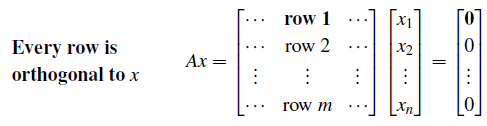위에서 row 1은 x와 orthogonal하다. 왜냐하면, 이 둘의 내적이 0이기 때문이다. 모든 우변이 0이기 때문에, row 1 ~ row m까지 x와 내적을 했을 때 0이 될 것이고, 따라서 x는 모든 row의 조합과 orthogonal하게 된다. Null space에 있는 x는 row space에 있는 각각의 벡터들과 orthogonal하기에, 다음과 같이 null space와 row space의 관계를 표기할 수 있다.
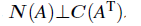가운데 'ㅗ'기호는 공간과 공간이 orthogonal 하다는 기호이다.
두번째로 살펴 볼 공간들은 left null space와 column space이다.
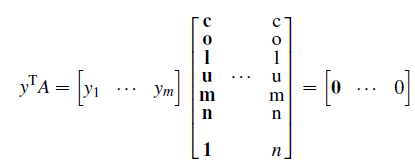벡터 y는 모든 column들과 orthogonal하다. 우변이 모두 0이기 때문에 y와 column 1 ~ column n까지의 내적은 0이 된다. 그래서 y는 모든 column의 조합과 orthogonal하고, 이는 다음과 같이 left null space와 column space의 관계를 표기할 수 있다.
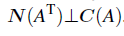이는 위에서 A를 A의 전치 행렬로 바꿔주면 같아지기에 성립한다.
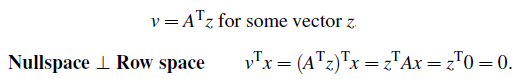만약 x가 null space에 있다면, Ax = 0이다. 그리고 만약 v가 row space에 있고, 행들의 조합으로 표현이 가능하다면, v는 위와 같이 벡터 z에 대해서 성립한다. 그렇게 되면 v와 x를 내적했을 때 0이 나오는 것을 확인할 수 있다.
두 공간 U, V가 직교하면 orthogonal 하다고 말할 수 있다. 그리고 부분 공간 V에 대해서 orthogonal한 벡터를 전부 모아놓은 부분 공간 U를 orthognoal component라고 하고 위와 같이 V perp라는 기호로 적어준다. 이 용어와 기호를 통해서 우리는 지금까지 공간들의 관계를 다음과 같이 표기할 수 있다.
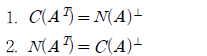1은 row space와 null space가 orthogonal하다는 의미이며, 2는 column space와 left null space가 orthogonal하다는 의미이다. Dimension은 어떠할까?
1은 r과 (n - r)의 합이므로 n이고, 2는 (m - r)과 r의 합이므로 m이다.
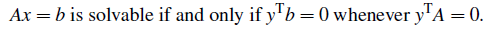이것은 당연한 사실이지만 알아둬야 할 필요가 있다. Ax = b가 해를 가진다는 말은 직교하는 y와 A를 만족시키는 y에 대해서 y와 b도 직교하다는 것과 동치이다.
간단하게 증명해보면, Ax = b가 해를 가진다고 가정하면 b는 C(A) 내에 있을 것이다. 이 때 벡터 y가 A와 직교하면, y는 A의 left null space에 있을 것이고, column space와 left null space는 orthogonal하므로, 벡터 y는 b와 직교할 것이다.
반대로, 벡터 y가 A와 직교할 때, 벡터 y가 벡터 b와 직교한다고 가정하자. 그러면 y는 A의 left null space에 있으므로, b는 직교하는 공간인 A의 column space에 있을 것이다. 따라서 Ax = b는 해를 가지게 된다.
Matrix and Subspaces
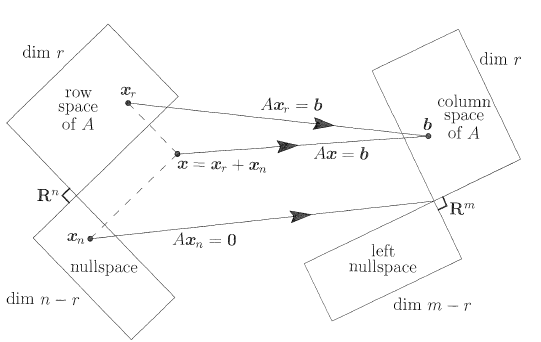m by n A를 linear transformation으로 생각해보면, n차원의 공간에서 m차원의 공간으로 transform 시키는 함수가 된다. 이때, 정의역은 row space, null space이고, 공역은 column space, left null space로 나눌 수 있다. 우리는 x를 row space의 x와 null space의 x의 벡터 합을 이용해서 쓸 수가 있다.
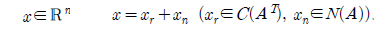여기서 Ax = b가 column space에 있게 된다면, 다음과 같이 된다.
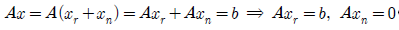즉, null space의 x는 A에 의해 전부 0으로 보내지고, row space의 x는 b로 보내지게 된다면 row space의 x와 null space의 x의 벡터 합으로 만들어진 모든 벡터 x는 b로 보내지게 된다. 따라서 A를 row space에서 column space로 transfrom해주는 함수라고 생각하면, 이는 일대일 대응 함수가 된다.
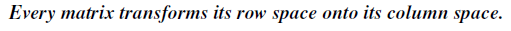이렇게 설명하면 어렵기 때문에, 예시를 통해서 위의 4공간이 어떠한 관계를 가지게 되는지 한번 살펴볼 것이다.
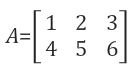A는 간단하게 2개의 행과 3개의 열로 구성된 행렬이다. 그러면 m = 2, n = 3이 되어, 2개의 방정식과 3개의 미지수가 존재하게 된다. 먼저 A의 row space를 보면 A의 행 벡터들의 linear combination으로 형성된 공간이다. n = 3이기 때문에 3차원 공간 상에 존재하게 된다.
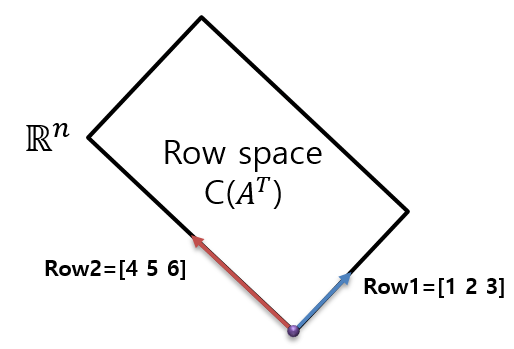Row space는 (1, 2, 3)과 (4, 5, 6)의 linear combination을 통해서 3차원의 공간상에 2차원의 평면을 채우게 될 것이다. 하지만, 2차원 평면을 채울 수 있지만, 3차원의 공간을 채우지 못하는데, 이 두 벡터와 직교하는 또 하나의 벡터가 존재하지 않기 때문이다. 여기서 두 행 벡터들과 직교해서 3차원의 공간을 형성할 수 있도록 하는 것이 바로 null space이다.
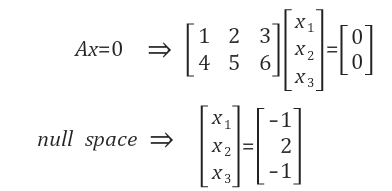위에서 null space는 (-1, 2, -1)이 span할 것이다. 그렇다면 이 벡터가 (1, 2, 3), (4, 5, 6)과 orthogonal한지 확인하기 위해서 내적을 해봐야 한다. 각각 내적을 하게 되면 둘 다 0이 되므로 이렇게 만들어진 3개의 벡터는 orthogonal하고 다음과 같이 3차원 공간을 형성하게 된다.
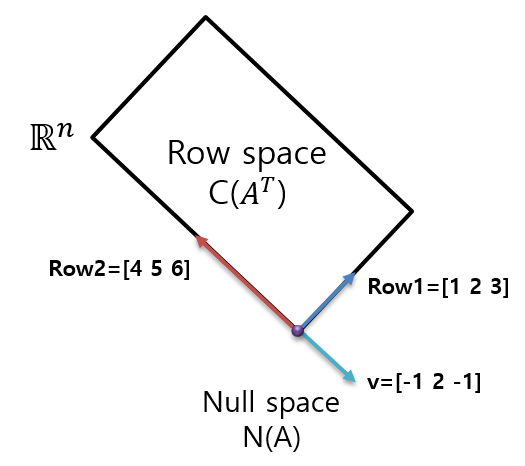A의 row space의 dimension은 rank와 같은 r이고, A의 rank는 2이기에 A가 정의할 수 있는 공간은 3차원의 공간상에 존재하지만, dimension에 의해서 2차원 평면인 것이다. A의 null space의 dimension은 n - r이기에 1이라서 1차원의 직선이 될 것이다.
A의 column space의 dimension은 row space와 같은 r이기 때문에, column space도 2차원이 될 것이다. 그렇다면 left null space는 어떠한가?
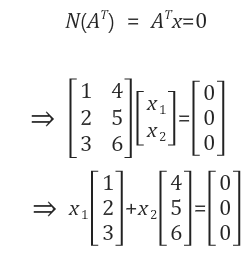위를 만족시키는 x벡터는 (0, 0)이 된다.
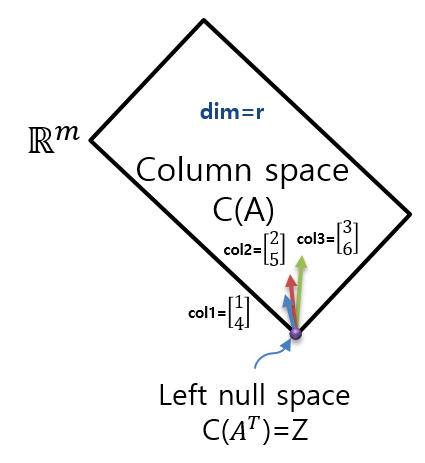A의 column space는 m차원의 공간 상에 존재하는데, column space의 dimension이 2이고, m이 2이기 때문에 left null space의 dimension은 자연스럽게 0이 된다. 이렇게 임의의 행렬 A가 주어졌을 때, 4개의 주요한 공간들의 orthogonal 관계에 대해서 알아보았고, 이 공간들의 특성과 관계를 잘 파악할 수 있어야 한다.
