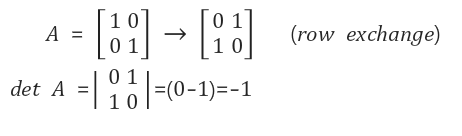선형 대수학을 공부하는 입장에서 행렬식이라고 하는 determinant는 어떠한 의미를 가지고 있는 것인가? 정의를 먼저 살펴보면, determinant는 정사각 행렬에 수를 대응시키는 하나의 함수로, 대략 정사각 행렬이 나타내는 선형 변환의 부피를 확대시키는 정도를 나타낸다. 이렇게만 이야기하면 굉장히 난해할 수 있다. 확실히는 모르겠지만, 무엇인가 결정하는 중요한 역할을 하는 함수 정도로 생각할 수 있다. 그냥 어떤 특별한 계산식에 따라서 행렬의 원소들을 대입해서 얻은 수치를 지칭하는데, 이 결과값이 그 행렬의 특성을 결정짓는 중요한 값이 된다. 그렇다면 determinant가 하는 역할이 무엇이 있을지 조금만 살펴보도록 하자.
1. Invertibility
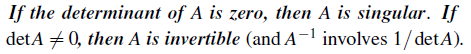어떤 행렬 A가 주어졌을 때, determinant가 0이면 singular하다. 즉, A는 invertible하지 않다는 것이다. Determinant가 어떤 행렬의 역행렬 존재 여부를 판단할 수 있기에 중요한 역할을 하고있다. 이 성질은 뒤에 가서 자세하게 살펴보도록 할 것이다. 왜냐하면, 꽤 중요한 성질이기 때문이다.
2. Volume
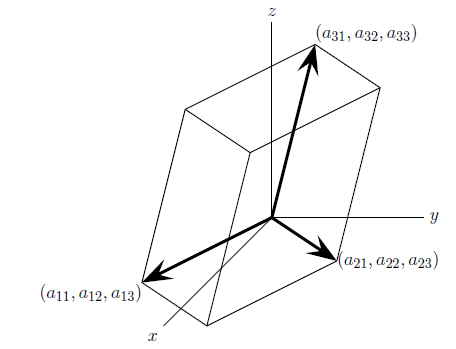n차원의 공간 상에서 determinant는 부피를 나타낸다. 기하학적인 해석으로 볼 수 있는데, 만약 determinant가 0이 되면 무슨 의미일까? 행렬을 구성하는 벡터가 0 벡터가 아닌데도, determinant가 0이라는 사실은 행렬을 구성하는 벡터들이 사실은 서로 동일한 선상에 있다는 것을 의미한다. 즉, 벡터가 해당 공간의 basis가 아님을 의미한다. 이 성질도 왜 determinant가 크기, 부피 등으로 이해할 수 있는지는 뒤에 자세하게 살펴볼 것이다.
3. Formula for each pivot
이론적으로, 우리는 pivot이 언제 0이 될지 예상할 수 있고, 이때 row exchange를 실행했었다.
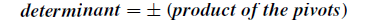Row exchange를 한다는 것은 determinant의 부호(sign)가 바뀌는 것을 의미한다. 어떤 행렬이든 임의의 row를 교환하면 determinant의 부호가 바뀌게 되는데, 부호가 +에서 -를 번갈아 결정이 된다. 이는 row exchange를 짝수번 진행했는지, 홀수번 진행했는지에 따라 정해진다. 쉬운 예시로 identity matrix를 row exchange를 진행하면 permutation matrix의 형태가 나온다.
