Determinant를 이해하는데 있어 몇가지 특성을 알아둬야 한다. 특성이 조금 많기는 하지만, 그렇게 어려운 내용은 아니다. 이해하기 쉽도록 가장 간단한 경우인 n = 2인 행렬에 대해서 살펴볼 것이다. 그리고 determinant는 모든 정방(square) 행렬에 대해서 다룰 것이다.
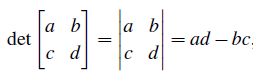우리에게 친숙한 2 by 2 행렬의 determinant는 위와 같이 계산할 수 있다. 행렬 앞에 "det"를 표기해주면, 이는 어떤 행렬의 determinant임을 의미하고, 2 by 2 행렬은 대각선의 곱끼리 뺄셈 연산을 해주면 된다. 이제 성질들을 차례대로 살펴볼 것이다.
1. The determinant of the identity matrix is 1
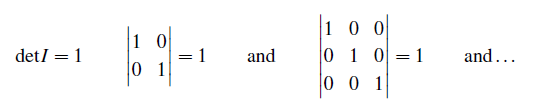모든 diagonal의 값이 1인 identity matrix의 determinant는 1이 된다. 이때 n by n 행렬에 대해서 동일하게 적용이 된다.
2. The determinant changes sign when two rows are exchanged
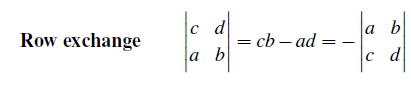행렬의 어떤 row를 다른 row와 바꾸면 determinant의 부호(sign)이 달라진다. 이 특성을 1번 특성과 합쳤을 때, identity matrix I의 row를 바꾸면 permutation matrix P가 되고, 결국 다음과 같이 P의 determinant는 (+1)과 (-1)이 된다.
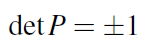이때 row exchange를 짝수번 했는지, 홀수번 했는지에 따라 부호가 정해질 것이다. 이는 임의의 n by n permutation matrix에서도 동일하게 적용이 된다.
3. The determinant depends linearly on the first row
임의의 행렬에 대해서 determinant를 구하는데 있어 linear combination의 규칙이 적용이 된다. 그리고 이 규칙은 첫번째 row에 대해서 해당이 된다.
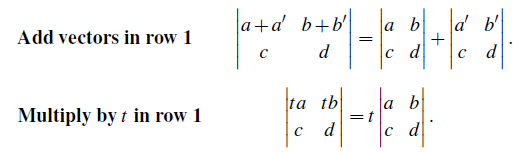위와 같이 첫번째 row에 대해서 덧셈과 곱셈은 linear combination의 규칙에 따라서 분리시킬 수 있다.
4. If two rows of A are equal, then detA = 0
이는 2번 특성으로부터 파생된 내용으로, 2개의 row가 동일할 경우에 다음과 같이 determinant는 0이 될 것이다.
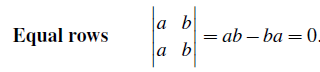2 by 2는 이해가 되지만, n by n은 어떠할 것인지 쉽게 이해가 되지 않을 것이다. 하지만 n by n 행렬의 경우에도 2개의 row가 동일하다면, determinant는 반드시 0이 될 것이다.
2번 특성에서 row exchange가 발생하면 원래의 행렬과 다른 행렬이 만들어지게 되고, determinant의 부호는 바뀌게 된다. 그러나 두 row가 같아져 버리면 row exchange를 해도 결과가 같아진다. 하지만 2번 특성을 만족하기 위해서는 부호는 바뀌게 될텐데, 원래 행렬과 바뀐 행렬의 부호를 바꿔도 행렬이 같기 때문에 determinant도 같아야 한다. 따라서 어떤 행렬이 2개의 row가 같게 된다면, determinant는 반드시 0이 되어야 같은 row를 바꾸더라도 특성 2를 만족하게 된다.
5. Subtracting a multiple of one row from another row leaves the same determinant
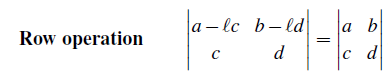이 특성은 3번 특성과 4번 특성으로부터 쉽게 만들 수 있다. 3번 특성과 같이 덧셈과 곱셈은 linear combination으로 나눌 수가 있으며, 이때 두번째 행렬의 row들이 같아진다.
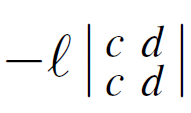이러면 4번 특성에 의해서 이 행은 자연스럽게 0으로 지워지게 되어 첫번째 항만 남게 될 것이다.
6. If A has a row of zeros, then detA = 0
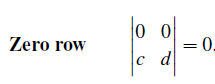6번 특성도 간단하다. 바로 원소들이 모두 0인 row가 한개라도 존재하면, determinant는 0이 된다. 0인 row가 있으면 이 행렬은 singular matrix가 되어 rank가 n보다 작아지게 되어 역행렬이 존재하지 않게 된다.
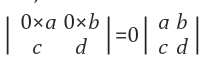이는 자연스럽게 3번 특성으로부터 유도할 수 있다.
7. If A is triangular then detA is the product of diagonal entries
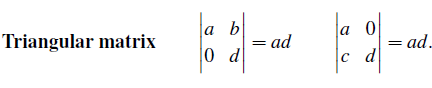만약 행렬이 triangular matrix라면, 즉 대각 성분을 제외하고 한쪽이 모두 0이 된다면 determinant는 모든 대각 성분의 곱이 된다.
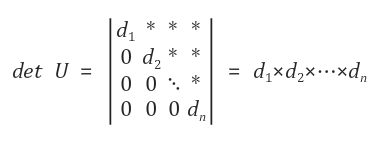추가로 신경써야하는 부분으로 determinant의 부호이다. U는 보통 elimination 과정을 거쳐서 만들어지고, 이 과정에서 row exchange가 여러번 일어날 수 있다. 만약 row exchange가 홀수번 일어나게 되면 결과에 마이너스(-) 부호를 붙여주면 된다.
8. If A is singular, then detA is 0. If A is invertible, then detA is not 0.
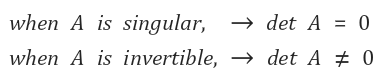7번 특성에서 대각 원소들이 0이 아님을 가정했고, 만약 하나라도 0이 된다면 determinant는 0이 된다. 이 경우 6번 특성에 의해서 행렬이 singular matrix임이 판명나게 되고, 따라서 singular일 때는 determinant가 0이 된다. 반대로 nonsingular, 즉 invertible하면 determinant는 0이 아니게 된다.
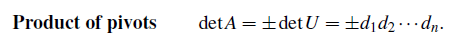여기서 이야기하고 싶은 것은, elimination을 통해서 upper triangular matrix를 만들게 된다면 대각 원소들의 곱으로 determinant를 쉽게 구할 수 있다. 주의해야할 부분으로 0인 row의 존재여부이고, 없다면 부호를 신경써서 determinant를 구하면 된다.
9. detAB = (detA)(detB)
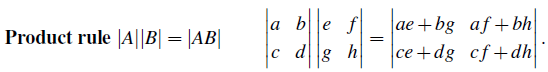행렬 A와 B의 곱의 determinant는 determinant A와 determinant B의 각각의 곱과 같다. 여기서 우리는 특별한 경우인 A의 역행렬의 determinant를 구할 수 있다.
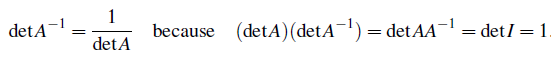다음의 예시를 보자.
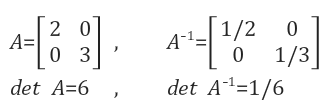정말로 간단하게 구할 수가 있다.
10. The transpose of A has the same determinant as A itself
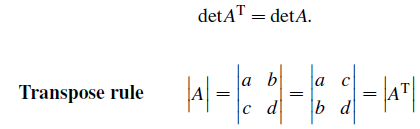Transpose matrix는 row와 column의 크기는 그대로이지만, 원소들이 바뀐다는 것이다. 지금까지 0인 row가 존재하면, determinant가 0임을 알아봤다. 이와 같이 0인 column이 존재하면 determinant는 0이 된다. 그리고 부호도 마찬가지로 column exchange를 통해서 바뀌게 된다. 우리는 PA = LDU라는 decomposition을 알고 있다. 이를 통해서 이 특성을 증명해볼 것이다.
우리는 9번 특성을 이용해서 각각을 determinant한 것과, transpose한 결과의 determinant를 한 것이 같음을 보이고 싶다.
L과 U의 determinant는 같을 것이고, 이를 transpose해도 triangular matrix이기 때문에 determinant는 대각 성분들의 곱일 것이다. 그리고 L과 U은 대각 성분들이 1이기 때문에 determinant는 1이 된다. D도 diagonal matrix이기 때문에 transpose를 취해도 determinant는 같다. 그래서 마지막으로 permutation matrix P만 같음을 보이면 된다. P는 I가 row exchange를 하여 생긴 것으로, P와 P의 transpose를 곱하면 I가 된다. 그래서 결론적으로 P와 P의 transpose는 반드시 같은 determinant를 가져야 하고, 결과적으로 A와 A의 transpose의 determinant도 같아야 한다.
