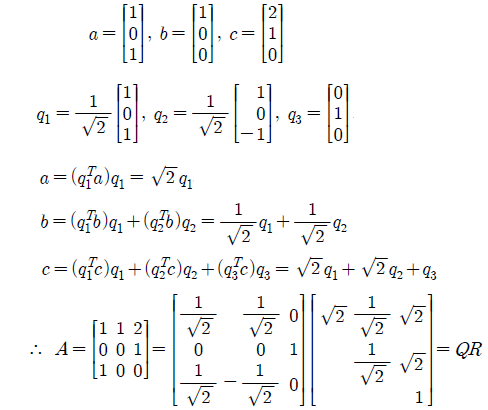지금까지 orthogonal과 관련해서 많은 이야기를 해봤는데, 이번에는 임의의 basis를 orthogonaal하게 바꾸는 과정을 진행할 것이다. 그리고 이 과정을 Gram-Schmidt process라고 한다. 그 전에 간단한 정의 하나 알고 가자.
벡터가 서로 orthogonal하고 각각의 길이가 1이면, orthonormal하다고 말하고, 행렬에서 column들이 서로 orthonnormal하면 이 행렬은 기호로 Q로 표기한다. 대표적인 예시로 identity matrix I의 column들이 서로 orthonormal하다는 것을 쉽게 알 수 있다. 그리고 이 columnn들을 e로 표기하여 standard basis라고 한다.
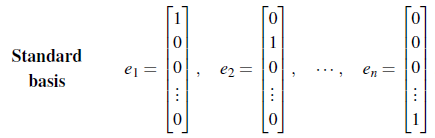
Orthogonal Matrices
행렬 Q의 column들이 orthonormal하기 때문에 다음과 같은 성질이 성립된다. 이때 행렬 Q는 정사각 행렬이어도 되고, 아니어도 된다.
특히, Q가 정사각 행렬 일 경우, Q를 orthogonal matrix라고 한다. 다음의 예를 보자.
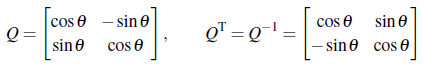Rotation matrix를 예시로 들어보면 Q가 orthonormal matrix라는 것을 쉽게 확인 할 수 있다.
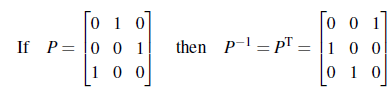또 다른 예로는 permutation matrix P가 있다. P의 column들은 standard basis이기 때문에, P는 orthogonal matrix이다. Orthogonal matrix의 성질을 알아두면 좋다.
- 벡터 x의 길이를 보존한다.
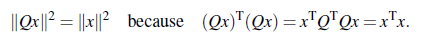
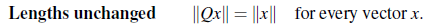
- 벡터 x, y 사이의 내적을 보존한다.
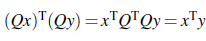
- 벡터 x, y 사이의 각도를 보존한다.
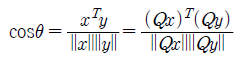
모든 내적과 길이는 보존이 되는데, 이는 공간이 rotation하거나 reflection해도 보존이 된다.
Rectangular Matrices with Orthonormal Columns
A가 정사각 행렬이 아닌 경우에 대해서 Ax = b에 대해서 알아보았다. 이번에는 Qx = b에 대해서 좀 더 자세히 알아보고자 한다. Qx = b에서 Q가 정사각 행렬이 아닌 경우에는 b가 C(Q)에 없어 해를 구할 수 없을 것이다. 이 경우에는 least square solution을 구하기가 오히려 쉽다.
벡터 p를 column form으로 적으면 다음과 같다.
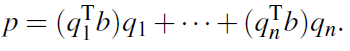즉, orthonormal basis q들에 대해서 임의의 벡터 b를 q들의 span에 대한 projection을 하면 위와 같이 표현이 되는 것이고, 이 표현은 Gram-Schmidt process에서 사용될 것이다.
Gram-Schmidt Process
우리의 최종 목표인 basis를 직교하게 만들려면 조작해주는 작업이 필요하다. 우리는 이를 Gram-Schmidt process라고 하고, 어떻게 하는지 알아볼까 한다.
n개의 벡터 v가 벡터 공간 V를 span하는 V의 basis라고 하면, 이들을 orthonormal한 basis q로 바꾸고자 한다. 아이디어는 간단하다. 하나의 벡터를 기준으로 잡고 나머지 벡터들을 기준 벡터와 직교하도록 만들어가면 된다.
첫번째 v를 q로 바꾸는 과정은 쉽다. 길이만 1로 만들면 되기 때문에 다음과 같이 자신의 길이로 나눠주면 된다.
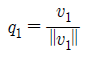그리고 보통은 다음 그림과 같이 2개의 벡터가 orthogonal 하지 않을 것이다. 그럼 첫번째 벡터에 orthogonal한 벡터를 먼저 찾아야 한다.
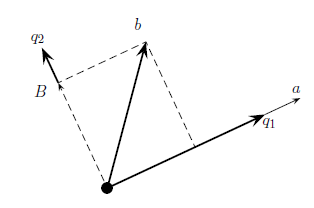위의 그림에서 a와 b가 서로 평행하지도, 직교하지도 않는다. a 방향으로 길이가 1인 첫번째 q는 쉽게 만들었다. 그렇다면 두번째 q는 어떻게 만들면 될까? 앞서 b를 a에 projection시킨다고 했을 때, 그 error가 a와 직교 한다는 조건을 통해서 projection point나 matrix를 구할 수 있었다. 그걸 이용해서 b를 a방향의 길이가 1인 첫번째 q에 projection시킬 것이다. 이때의 error를 B로 하면, B는 첫번째 q와 orthogonal하고, 이를 다시 자신의 길이로 나누어 두번째 q를 만들 수 있다.
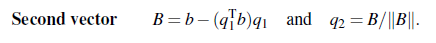이렇게 첫번째 q와 두번째 q를 만들었으면, 세번째 q도 만들 수 있다. 아무래도 모든 벡터가 서로 직교해야하기 때문에, 세번째 q는 첫번째와 두번째 q와는 같은 평면에 있지 않을 것이고 직교해야 한다.
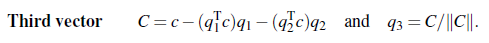이러한 아이디어들이 전체 Gram-Schmidt process의 과정이다. 네번째가 추가 된다면, 위와 같이 하나의 항을 더 빼주면 된다. 예를 보자.
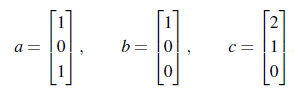첫번째 q는 a를 이용해서 만들 것이다.
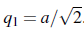이를 이용해서 두번째 q를 구할 것이다.
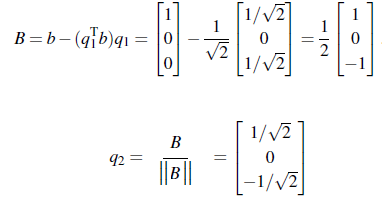이를 이용해서 세번째 q도 구하면 된다.
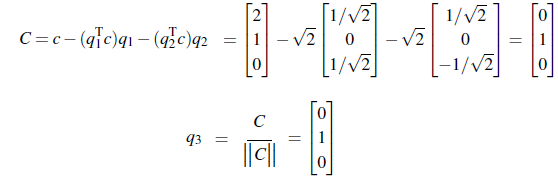사실 이미 unit vector이기에 그 자체로 세번째 q가 된다. 이렇게 만든 3개의 벡터를 이용해서 orthonormal matrix Q를 만들면 된다.
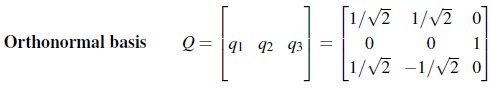이거는 이제 일종의 경험인데, 위와 같이 a, b, c가 주어졌을 때 굳이 a를 기준으로 하지 않아도 된다. 다만 어느 벡터를 기준으로 했을 때 더 계산이 쉬운지 생각하고 진행하면 쉽게 Gram-Schmidt를 진행할 수 있다.
Factorization A = QR
행렬 A가 주어졌을 때 LU factorization을 통해서 A를 일종의 인수분해하는 것과 같은 분해하는 작업을 했었다. 여기서 우리는 A가 linearly independent하다고 가정한다. 그러면 이제 A의 column들을 이용해서 우리는 Gram-Schmidt process를 진행할 수 있고, 이를 통해서 A의 column들을 orthonormal vector로 바꿀 수 있다. 그렇게 바꾸는 과정에서 부가적인 행렬이 생기는데, 이를 R이라고 표기하여 A = QR factoriztion을 진행할 것이다.
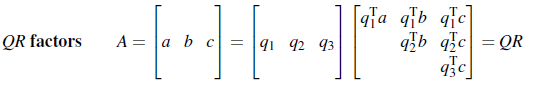A = LU와 비슷하지만 Q가 orthonnormal column들로 이루어져 있다. 그리고 R은 upper triangular matrix U와 같이 오른쪽 위로 0이 아닌 원소들이 존재하기 때문이다. 간단하게 다음 행렬을 QR factorization 해보자.
