Formulas
이제 determinant의 여러 식들에 대해서 알아보고자 한다.
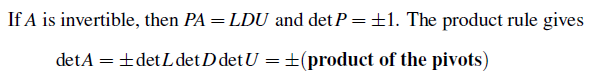이전에 A를 PA = LDU로 나눌 수 있다고 했다. 이때 D는 pivot들이 대각 원소로 존재하는 행렬이고 L과 U의 대각 원소들은 전부 1이기 때문에 determinant를 구하면 1이 될 것이다. 그래서 detL, detD, detU의 곱은 pivot들의 곱이 될 것이다. 그리고 부호는 P의 영향으로 row exchange가 얼만큼 일어났는지에 따라 결정이 된다.
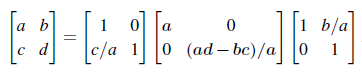2 by 2 행렬을 LDU 분해를 하면 위와 같이 일반화 할 수 있을 것이다. Pivot들의 곱은 ad - bc가 되고, 이것이 D 행렬의 determinant가 된다.
n이 2인 경우, determinant는 ad - bc가 되는 것을 알고 있다. 그렇다면 n이 3인 경우는 어떻게 determinant를 구할 수 있을까. 결과부터 이야기하면 다음과 같이 구할 수 있다.
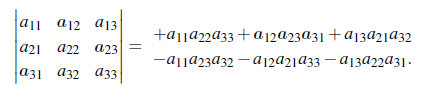총 6개의 항으로 구성되어 있음을 확인할 수 있는데, determinant의 몇가지 특성들을 이용하면 일반화시킬 수 있다.
시작하기에 앞서, 각각의 row가 다음과 같이 벡터들의 합으로 분해된다는 사실을 알고 있어야 한다.
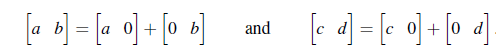이 사실은 determinant의 특성 중에서 첫번째 row에 대해서 determinant가 linearly dependent하다는 사실로부터 알 수 있다. 벡터는 하나의 row로 구성이 된 행렬로 볼 수 있기에, 이를 분해하는 것은 당연시 된다.
놀랍게도 이 사실은 행렬이라면 어떠한 행에서도 가능하다. 왜냐하면 행렬은 row exchange가 가능하기 때문이다.
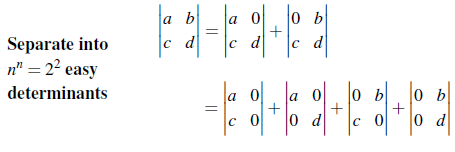분해를 시키다보면 기하급수적으로 계산량이 많아지는 것을 알 수 있다. 그리고 determinant의 특성 중에서 0인 row와 column이 존재하면 determinant가 0이 된다는 사실을 알고 있다.
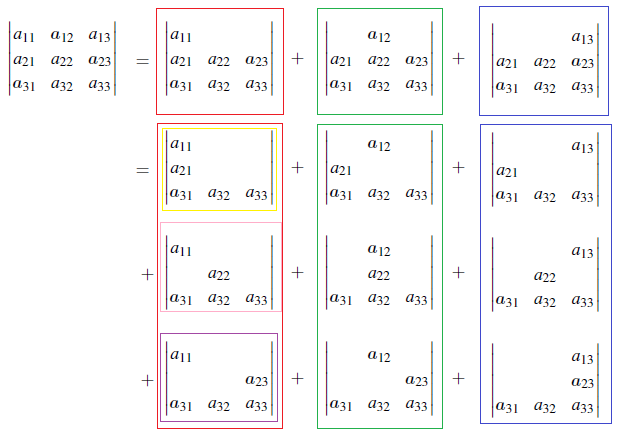
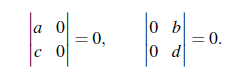이러한 사실들을 기반으로 해서 3 by 3 행렬의 determinant를 구할 것이다. 그리고 다음과 같이 계산을 하면 최종적으로 6개의 항이 남을 텐데, 이는 n을 확장해보면 알겠지만 2n개의 항으로 일반화가 가능하다.
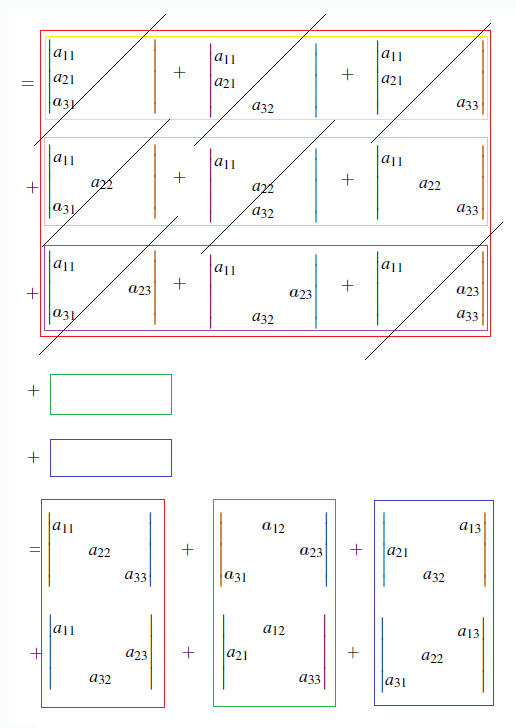
특성들을 활용해서 분해하다보면 다음과 같이 column이 전부 0인 determinant가 나올 것이다. 이러면 이 항들은 전부 0이 되어 처음 3개로 분해한 결과 각각에 대해서 2개씩의 항만 살아남게 된다.
따라서 3 by 3의 경우에는 3! = 6개의 determinant를 계산해주면 된다. 위에서도 2 by 2의 경우 2! = 2개의 determinant를 계산해준 셈이다. 그렇다면 4 by 4 행렬은 4! = 24개의 determinant를 계산해주면 된다.
이는 최종적으로 column이 0인 determinant 항들을 제거한 개수이고, 그렇다면 처음에 분리했을 때는 몇 개의 determinant로 분리하는지도 일반화할 수 있다. 2 by 2의 경우 4개, 3 by 3의 경우 27개였다. 즉, n의 n 제곱개만큼 분리할 수 있기에 4 by 4는 256개일 것이다. 물론, 이 많은 determinant 항들을 계산할 때 일일이 분리해서 하면 너무나도 귀찮을 것이다. 위에서 본 것과 같이 column이 0인 항들이 많이 생길 것이기에, 실제로 계산하는 determinant는 256개 중에 24개 뿐이다.
그렇다면 어떠한 determinant들이 0이 아니게 되어 살아남는 것일까?
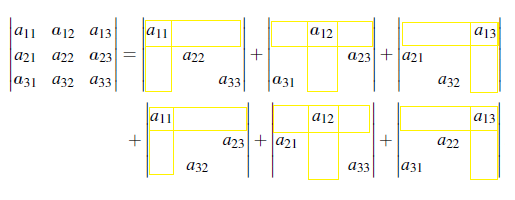각 원소들이 row와 column에 오직 자기 자신만이 존재하는 determinant만이 살아 남게 된다. 당연한 이야기일 수 있지만 뭔가 식으로 정립되지 않는 것 같다. 그래서 determinant를 식으로 일반화한 것이 있는데, 바로 다음에 볼 big formula이다. 위에서 3 by 3의 경우 살아남은 column들을 숫자로 적어보면 다음과 같다.
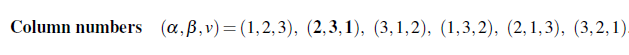숫자로 적어보니 어떠한 규칙이 보이지 않는가? 바로 (1, 2, 3)의 6가지 permutation들이다. 즉, (1, 2, 3)을 순서를 바꿔가는 것이고, 이를 행렬로 바라보면 permutation matrix P의 6가지 형태임을 알 수 있다. 그리고 우리는 모든 a를 다음과 같이 인수로 뺄 수 있고, 그렇게 되었을 때 곱해지는 determinant들은 permuation matrix의 형태를 취한다.
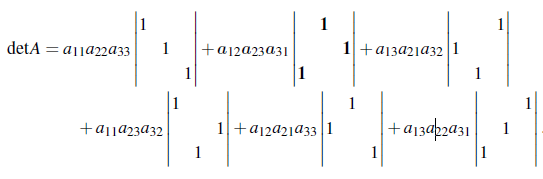그래서 우리는 이를 일반화 하여 다음과 같이 big formula라고 정의할 것이다.
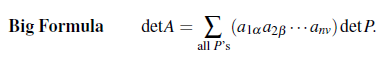Permuation matrix는 row exchange를 통해서 만들어지게 되는데, 이러면 부호의 변화가 생기게 된다.
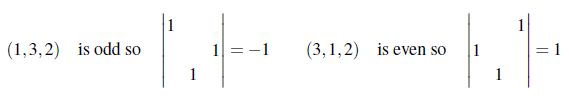(1, 3, 2)는 두번째 row와 세번째 row를 바꾼 것으로 홀수번에 해당하기에 부호는 마이너스가 붙을 것이다. 이렇게 해서 다시 처음의 3 by 3 행렬의 determinant를 보면 반은 양의 부호, 반은 음의 부호를 가지는 것을 알 수 있다.
우리는 여기서 새로운 개념을 알아볼 것이다. 바로 여인수(Cofactor)이다. Cofactor는 big formula를 분리하는 방법에서 사용되며, n by n의 determinant를 계산할 때 (n - 1) by (n - 1)의 determinant로 분리해가면서 계산할 때 다음과 같이 사용된다.
Cofactor는 우리가 column과 row에서 자기 자신만 존재하는 항들을 찾을 때, 3 by 3이라면 해당 column과 row를 지운 2 by 2의 행렬의 determinant가 된다. 그래서 위에서 n by n이 (n - 1) by (n - 1)로 분리해가면서 계산한다. 즉, 우리는 n을 줄여가면서 더 쉬운 determinant 계산들을 이용해서 n에 대한 determinant를 구한다고 생각하면 쉽다.
Expansion of detA in Cofactors
위에서 우리는 factor를 첫번째 row에 있는 원소들로 잡았었다. 그렇다면 두번째나 그 이상의 row의 원소들을 factor로 잡으면 안되는 것일까? 결론부터 이야기하면 우리는 어떠한 row를 factor로 잡아도 해당하는 row와 column을 지우고 나머지 원소들로 하나 작은 determinant들을 계산해도 결과는 같다. 첫번째 row를 잡아서 하는 이유는 아무래도 계산의 편의성 때문이다. 다른 row를 잡아서 할 때는 대신 부호만 주의해주면 된다. 이 부호를 정할 때도 일반화하는 식이 존재한다.
앞서 첫번째 row를 factor로 잡았을 때 부호는 +, -, +가 나왔다. 이를 일반화 하면 첫번째 row에 대해서는 다음과 같이 cofactor를 정의할 수 있다. 여기서 i는 row, j는 column에 해당한다.
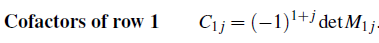그리고 이를 일반적인 row i에 대해서 정의하면 다음과 같다.
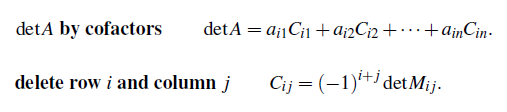결국 어떠한 row를 잡았을 때, 그 row와 각각의 column에 대해서 i + j가 홀수가 되면 음의 부호가 붙고, 짝수가 되면 양의 부호가 붙게 된다. 역시 예를 통해서 살펴보면 이해가 쉽게 될 것이다.
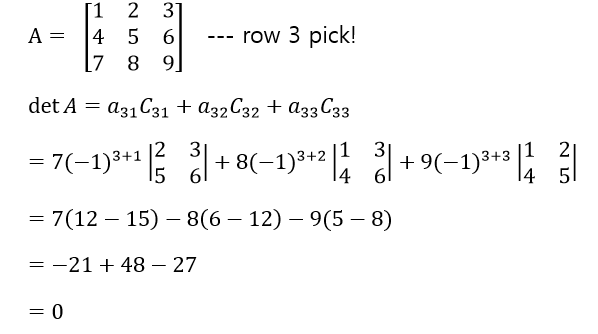
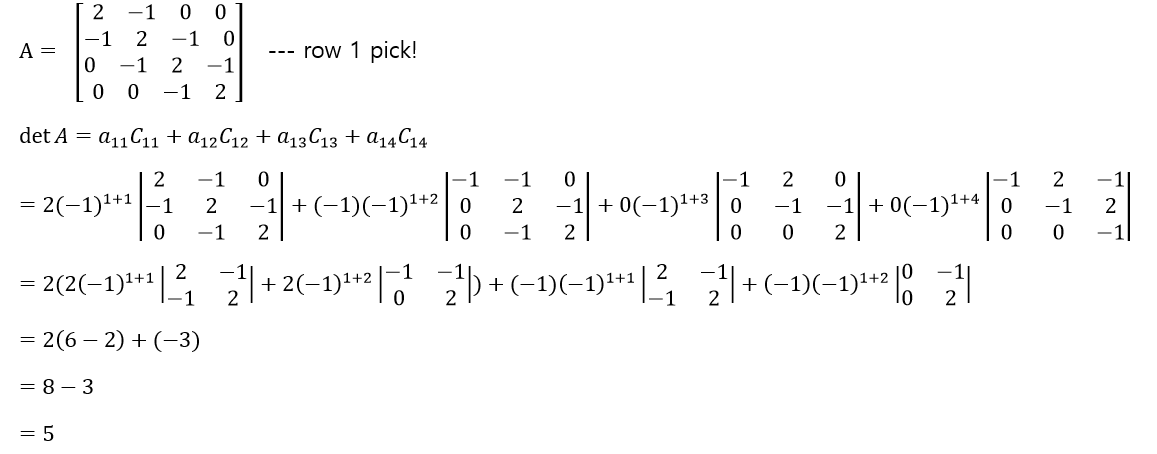결과적으로 계산의 편의성을 위해서라면 0이 많이 존재하는 row를 선택하는 것이 좋다. 0의 존재는 determinant의 계산의 효율성을 증가시켜준다.
