역행렬(Inverse Matrix)
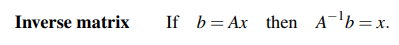역행렬을 원래 행렬과 곱하게 되면 단위 행렬(I)가 나오게 된다. 이 사실은 누구나 알고 있을 것이다. 그렇다면 여기서 주목할 것은 역행렬의 존재성에 대한 것이다. 모든 행렬이 역행렬을 가지지는 않는다. 만약에 AX는 0이고 x는 0이 아니라면 역행렬은 존재할 수 없다. 어떠한 행렬도 0인 AX 벡터와 곱해서 0이 아닌 x 벡터를 만들지 못할 것이다. 우리의 목표는 역행렬을 정의하고 계산하고 또 그것을 사용하는 것까지이다. 그러기 위해서는 역행렬의 존재성에 관심을 가져야하며, 어떠한 행렬이 역행렬이 없는지 알아볼 것이다.
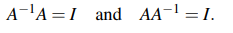위의 식은 기존의 행렬 A와 그 역행렬을 곱하게 되었을 때 단위 행렬이 되는 것을 말해준다. 처음식은 A의 왼쪽에 역행렬이 붙어 있는데, 이를 Left Inverse라고 부르며, 두번째 식은 A의 오른쪽에 역행렬이 붙어 있는데, 이를 Right Inverse라고 부른다.
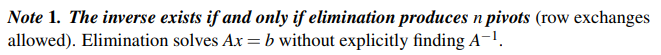이 사실은 반드시 알고 가야 한다. 행렬이 역행렬을 가지기 위해서는 Elimination 이후에 정확히 n개의 피벗을 가져야 한다.
A의 역행렬은 두가지가 될 수 없다는 것이다. 즉, A의 역행렬은 유일하다는 것이다.
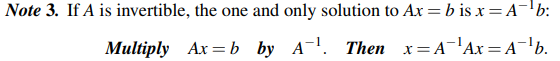우리는 invertible하다는 말을 자주 사용하게 될 것인데, 이는 A가 역행렬을 가질 수 있다는 것을 의미한다. 그래서 A가 invertible하다는 말은 x는 유일하다는 말과 동치이다.
그리고 만약 0이 아닌 벡터 x가 있는데, Ax = 0 이라고 한다면, A는 역행렬을 가질 수 없다는 이야기이다. 만약 A가 invertible하다면, Ax = 0은 유일한 해인 x = 0을 가지게 된다. 이 둘을 헷갈리면 안된다. 역시나 중요한건 A 역행렬의 존재성이다.
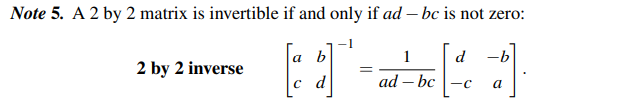그리고 n = 2인 행렬에서 역행렬을 구하고 싶을 때, 위와 같은 공식을 사용하면 바로 구할 수가 있다. 여기서 분모항에 들어가는 ad - bc를 우리는 determinant라고 부르며, 이것을 통해서 invertible한지 안한지 알 수가 있다. 이것이 0이 된다면 invertible하지 않은 것이고, 0이 아니라면 invertible한 것이다. 자주 사용되니 알아두면 좋다.
대각 행렬같은 경우는 어느 대각 원소도 0이 아니라면, 역행렬을 위와 같이 분자 분모를 바꿔주면서 쉽게 구할 수 있다.
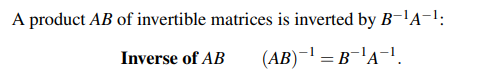역행렬을 곱해나갈 때 주의해야하는 점은 순서이다. 보통 반대로 곱해나간다고 생각하면 이해하기 쉬울 것이다. 이를 증명하는 과정은 아래에 있는데, 어렵지 않으니 읽어보면 될 것이다.
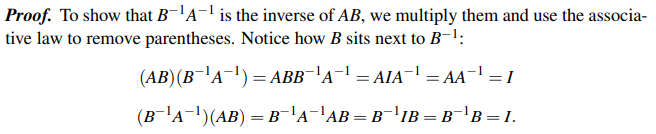그렇다면 3개는 어떨까?
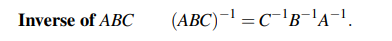순서가 반대로 된다는 사실은 변함이 없다. 몇개를 곱하든 똑같기 때문에 순서가 반대로 된다는 사실만 기억하면 된다.
Gauss-Jordan Method
위에서 n = 2인 정사각 행렬의 역행렬은 쉽게 구하는 방법을 알았고, 대각 행렬도 쉽게 역행렬을 구할 수 있었다. 그렇다면 일반적인 정사각 행렬의 역행렬은 어떻게 구할 수 있을까? 역행렬을 구하는 방법은 2가지가 있는데 그 중 하나가 바로 Gauss-Jordan Method이다. 이 과정에서 앞에서 배운 Gaussian Elimination이 필요할 것이다.
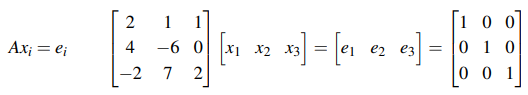역행렬의 정의를 생각했을 때, 위에서 x는 A의 역행렬이어야 하고, e는 단위 행렬이어야 한다. 우리는 X를 찾고 싶은 것이다. 정확하게는 ei는 I의 i번째 열인 셈이다. x도 마찬가지이다. 다음의 예시를 통해서 어떻게 역행렬을 구하는지 볼 것이다. 우리는 A와 I의 곱셈 결과가 I와 A의 역행렬의 곱셈 결과가 같다라는 사실로부터 차근차근 형태를 만들어가면서 구할 것이다.
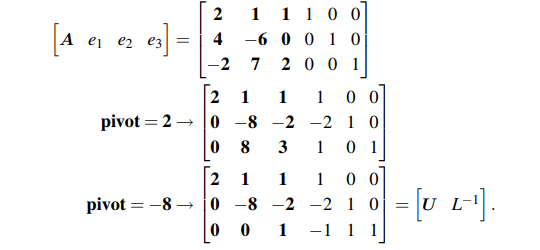첫번째 과정은 A 행렬을 U로, I 행렬을 L의 역행렬로 바꿔주는 과정이다. 대괄호 안에 A와 I를 처음에 적은 뒤에 Gaussian Elimination을 동시에 진행해주면 된다. 그렇게 했을 때 I는 자연스럽게 L의 역행렬로 만들어질 것이다.
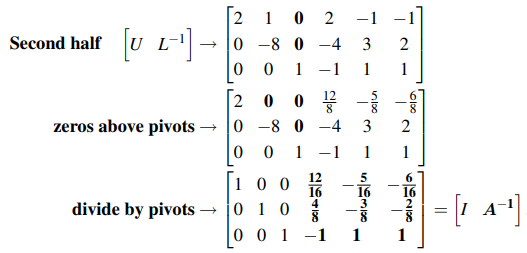두번째 과정은 U 행렬을 D를 거쳐 I로 만드는 과정으로, 이 과정을 진행해주다 보면 L의 역행렬로부터 자연스럽게 어떤 행렬이 만들어 질 것인데, 전체 구조를 봤을 때 이 행렬은 A의 역행렬이 될 것이다. 다만 이 과정에서 식이 좀 복잡해 질 수 있는데, 유의하면서 Gaussian Elimination을 진행해주면 된다.
전치행렬(Transpose Matrix)
전치 행렬(Transpose Matrix)는 역행렬과 비슷하면서도 조금 더 간단하다. 쉽게 생각하면 행렬을 상하좌우 대칭 시켜놨다고 생각하면 된다. 전치 행렬의 원소는 기존 행렬에서 행과 열의 인덱스 값만 바꿔주면 된다.
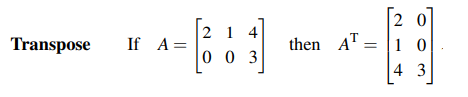
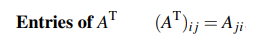이제 몇가지 성질에 대해서 볼텐데, 만약 2개의 행렬을 더하고 전치시키면 어떻게 될 것인가? 
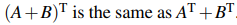그냥 각각을 전치 행렬로 바꾼 뒤에 더한 것과 결과가 같다. 그렇다면 곱셈과 역행렬은 어떻게 되는가?
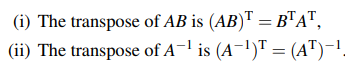덧셈과는 다르게 곱한 뒤에 전치 행렬로 바꾸면 각각의 전치행렬의 곱이긴하나 순서가 바뀌게 된다. 이전에 행렬의 곱셈에서 교환 법칙은 성립이 안된다는 것을 알았을 것이다. 그만큼 행렬에서는 곱하는 순서가 중요하다. 역행렬의 전치 행렬같은 경우 전치 행렬의 역행렬과 결과가 같은 것을 볼 수 있다. 이는 다음의 간단한 증명 과정을 통해서 알 수 있다.
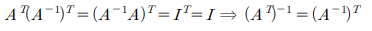
대칭행렬(Symmetric Matrix)
전치 행렬이 상하좌우 대칭 시킨 결과라고 했는데, 그렇다면 대칭 행렬은 어떠한 행렬을 대칭 행렬이라고 하는 것일까? 전치 행렬과 대칭 행렬은 이름만 보았을 때 이 둘이 같은 것이 아닌가 싶지만, 사실 반은 맞고 반은 틀린 이야기이다.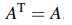 
대칭 행렬의 정확한 정의는 자신의 전치 행렬과 원래 자신의 행렬이 같은 행렬을 대칭 행렬이라고 말한다. 쉽게 말해서 A라는 행렬이 이을 때, 이를 전치 행렬로 바꿨는데도 똑같은 결과가 있다면 대칭 행렬이라고 하면 된다.
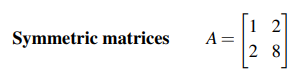
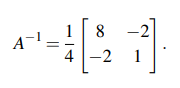위의 예시를 보면, 대칭 행렬의 역행렬을 구했는데, 역행렬을 자세히보니 이 또한 대칭 행렬의 형태이다. A와 A의 역행렬이 같다는 것이 아니다. A가 대칭 행렬이니 A의 역행렬도 대칭 행렬이라는 것이다. 대칭 행렬이 꼭 invertible할 필요는 없다. 그러나 invertible하다면 자연스럽게 대칭 행렬이 된다.
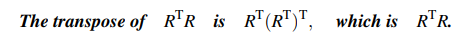m개의 행과 n개의 열로 이루어진 행렬 R이 있을 때, 전치행렬 R과 R의 곱셈과 R과 전치 행렬 R의 곱셈은 모두 대칭 행렬이 된다. 다음의 간단한 증명 과정을 통해서 확인할 수 있다.
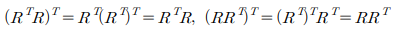간단한 예시를 보면 이해가 빠를 것이다.
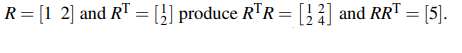다음은 알아두면 좋은 이야기를 해볼까 한다.
어떤 행렬 A가 invertible하고 symetric(대칭 행렬이 존재할 수 있는)하며 row exchange가 없을 때, LDU Factorization시에 U는 L의 전치 행렬이라는 것이다. 기본적으로 U와 L의 구조는 대칭 행렬을 떠오를 수 있는 구조이다. 이때 A가 앞의 조건을 만족하게 되는 경우에 한에서 둘은 대칭 행렬 사이를 만족하는 것이다.
