Triangular Factors
우리의 목표인 Ax = b를 풀기 위해서 계속해서 나아가고 있다. 이번에 볼 내용은 A를 LU 구조로 Factorization하는 것이다. 다항식에서 생각했을 때 인수분해와 같은 메커니즘이라고 보면 이해하기 쉬울 것이다. A를 이렇게 구조를 바꾸려는 이유는 Ax = b의 계산 횟수를 줄이기 위해서이고, 더 나아가 PA = LDU Factorization 까지 보려고 한다. 아래의 예시를 한번 보자.
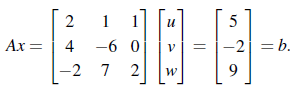우리는 여기서 3번의 Gaussian Elimination을 진행할 수 있다. 자세한 계산 과정은 생략하고 결과를 보면 다음과 같다.
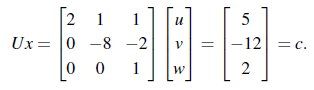여기서 A가 U로 바뀌었는데, U가 의미하는 것은 상삼각행렬(Upper Triangular Matrix)로, 말 그대로 대각선을 그었다고 생각했을 때 위에는 원소가 존재하고, 아래의 원소는 0이 되는 행렬을 말한다. 즉, 대각선(Diagonal)아래는 전부 0인 행렬이다.
위에서 3번의 단계를 했을 때 생기는 기본 행렬(Elementary Matrix)을 E, F, G 라고 하면 이는 다음과 같이 적을 수 있다.
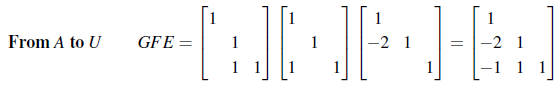E는 첫번째 행과 두번째 행의 연산, F는 첫번째 행과 세번째 행의 연산, 그리고 G는 두번재 행과 세번째 행의 연산임을 알 수 있다. 여기까지 꽤 괜찮게 진행이 되었지만, 정작 가장 중요한 포인트는 반대이다. 우리는 U로부터 어떻게 A를 찾아낼 수 있을까? A로부터 U를 찾는 과정이 GFEA = U 였다면, U로부터 A를 찾는 과정은 결론부터 말하면, 다음과 같이 역행렬을 차례로 곱해나가면 된다.
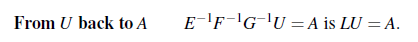그리고 여기서 우리는 기본 행렬에서 대각 성분을 제외한 값의 부호를 바꿔 기존의 기본 행렬과 곱하게 되면 단위 행렬(Identity Matrix)가 나옴을 알 수 있다.
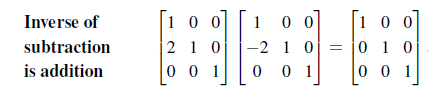놀라운 것은 U에 곱해진 단위 행렬의 역행렬들이 L이라는 것이다. L은 하삼각행렬(Lower Triangular Matrix)로, U와는 반대로 대각선을 기준으로 위의 성분이 전부 0이다.
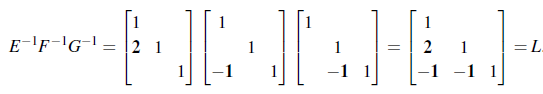그리고 L에서 주목해야 할 부분은 대각선 아래의 원소들이 Gaussian Elimination에서 뺄셈 연산을 진행할 행에 곱한 승수(Multiplier)들이라는 것이다.
조금더 재미있는 성질들을 살펴보면 U의 대각 성분들은 Gaussian Elimination의 피벗(Pivot)들이다. 그리고 알아두면 좋은 것이 Lower Triangular Matrix끼리의 곱은 다시 Lower Triangular Matrix가 되고, Lower Traingular Matrix의 역행렬도 Lower Traingular Matrix이다.
그리고 정말 중요한 내용 중 하나는, A = LU Factorization에서는 행 교환을 하지 않을 때만 가능하다는 것이다.
우리는 n = 2, 3인 경우만 볼 것이 아니라 더 확장해서 일반적인 경우도 생각하고 싶다. 아래는 n = 4인 경우이고, 이 경우에도 똑같이 Gaussian Elimination이 적용된다.
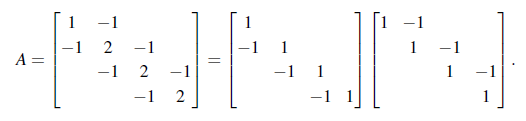
One Linear System = Two Triangular Systems
지금까지 Ax = b가 Gaussian Elimination에 의해서 Ux = c로 바뀌는 것을 확인했다. 그리도 기본 행렬들이 합쳐져 L이 됨으로써 A = LU Factorization까지 알아봤다. Ux = c의 양변에 L을 곱하면 LUx = Lc가 되는데, LUX = Ax이므로 Lc = b로 놓을 수 있다. 여기서 우리는 Ax = b를 Lc = b 와 Ux = c로 나누어서 생각할 것이다.
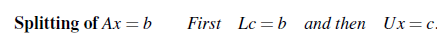우리가 이렇게 하는 이유는 L과 U가 Lower, Upper Triangular Matrix이기 때문에 Elimination이 필요 없이 바로 후방 대입(Back Substitution)을 하기 때문에 계산 횟수가 정말 많이 줄어든다.
순서를 보면 Ax = b에서 A를 LU로 바꾸면서 Lc = b와 Ux = c로 나누고, Lc = b에서 L과 b를 이용해서 c를 구하고, 이 c를 이용해서 Ux = c 에서 U와 함께 x를 구하면 되는 것이다.
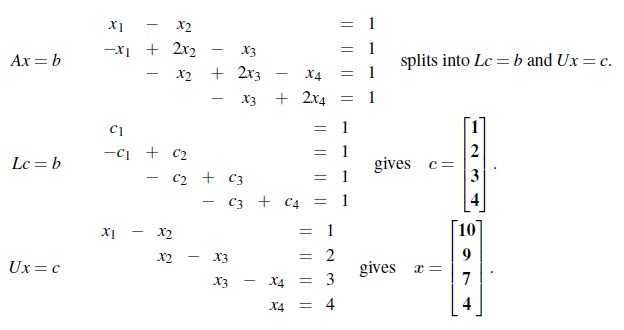우리가 알고가야하는 사실 중에서 Lower Triangular Matrix의 대각 성분은 전부 1이라는 사실이다. 그런데 Upper Triangulr Matrix의 대각 성분은 A의 피벗이라는 사실이다. 이 차이를 알아둬야 한다.
그래서 U를 다시 다음과 같이 나눌 것이다.
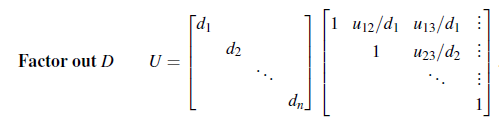즉, U에 피벗들을 대각선에 놓고 나머지에 0을 놓은 대각 행렬(Diagonal Matrix) D와 i번째 row를 i번째 피벗으로 나눈 행렬의 곱으로 나타낼 수 있다. 결국 U = DU로 새롭게 됨으로써 이 경우에는 A = LDU Factorization이 된 것이다. LDU 상태에서 L과 U의 대각 성분은 항상 1이어야 하고, unique 하다는 것을 알아두면 좋다. Unique 하다는 것은 오직 한가지 경우만 존재하는 것을 말한다.
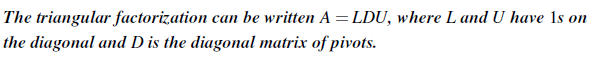
Row Exchanges and Permutation Matrices
Gaussian Elimination을 할 때 피벗 자리에 0이 올 경우에 앞에서는 Singular case 이거나 Row Exchange를 통해 계속 단계를 진행하는 case로 나눌 수 있다고 했다. 앞에서 Gaussian Elimination의 한 단계를 알려주는 역할을 하는 행렬로 기본 행렬(Elmentary Matrix)의 존재를 알게 되었는데, 여기 Row Exchange의 역할을 해주는 행렬도 이제 알아보려고 한다. 아래의 예시를 보자.
위의 식을 행렬로 바꾸고 순서를 바꾸고 싶다면 다음과 같이 순서를 바꿀 수 있도록 어떤 행렬을 곱해줘야 한다.
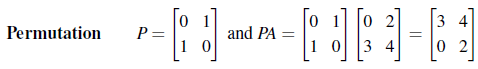이러면 기존의 Ax = b가 P라는 행렬에 의해 PAx = Pb가 된다. 여기서 P는 치환 행렬(Permutation Matrix)이며, 이 행렬로 인해서 행의 순서를 바꿀 수 있다. 즉, 앞으로 우리는 Row Exchange가 필요한 경우에는 PA = LU Factorization을 하면 된다.
만약 순서를 여러번 바꿔야 하는 경우 P도 여러개를 사용할 수 있다.
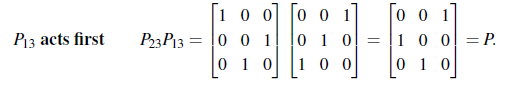그러나 순서를 여러번 바꾸다 보면 결국 기존의 결과와 같기 때문에 기본 행렬(Elementary Matrix)의 경우와는 다르게 많지는 않을 것이다.
PA = LU Factorization 은 어떤지 다음의 예시를 보면서 기존의 과정들을 생각하면서 풀어보면 좋을 것 같다.
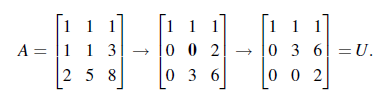첫번째 행에 1을 곱해서 두번째 행과 뺄셈 연산을 진행하면 두번째 행의 첫번째와 두번째 열의 값이 0이 되는 것을 볼 수 있다. 즉, 두번째 피벗 자리에 0이 오기 때문에, 이 경우에는 Row Exchange를 해줘서 새롭게 U를 만들어준다. 다음의 P를 이용해서 다시 PA로 Gaussian Elimination을 진행해보면 다음과 같다.
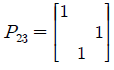위의 P를 이용해서 새롭게 만든 PA에 Gaussian Elimination을 진행하면 U를 만들 수 있고, E의 역행렬을 곱해줌으로써 PA = LU Factorization을 진행할 수 있다.
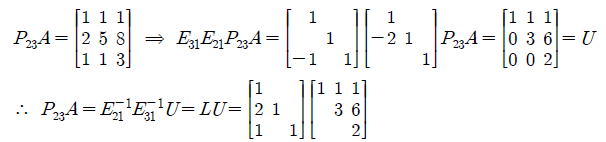그리고 한단계 더 가서 U를 DU로 만들면 다음과 같다.
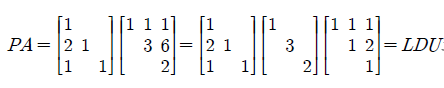Gaussian Elimination을 하면서 필요한 Row Exchnage의 개수에 따라 P의 부호(Sign)이 바뀌는데, 필요한 개수가 짝수이면 Sign = +1이고 홀수이면 Sign = -1이다.
