벡터 공간(Vector Space)
지금까지 A가 정사각 행렬인 경우에 대해서 Ax = b의 해를 구했다. 지금부터는 행렬을 정사각행렬에서 행의 길이가 m이고, 열의 길이가 n으로 확장해 일반적인 Ax = b를 풀어볼 것이다. 그러기 위해서는 벡터 공간(Vector Space)라는 개념이 필요하여 이에 대해서 알아볼 것이다.
벡터 공간은 벡터들을 모아놓은 집합으로 다음 2개의 연산에 대해서 닫혀있다. 여기서 '닫혀있다'라는 표현은 어떤 연산을 해도 그 범위 내에서 답이 나온다는 것이다. 간단하게 생각하면 자연수 범위 내에서 덧셈 연산은 닫혀있다. 1과 2를 더한 3도 자연수이기 때문이다.
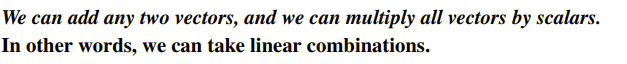벡터 공간에서는 더하기(Addition)와 실수 곱(Multiplication by Scalars)에 대해서 닫혀 있어야 한다. 즉, 주어진 집합이 벡터 공간인지 아닌지 판단하기 위해서는 위의 조건을 만족시키는, 즉 더하기와 실수 곱이 닫혀있는지만 확인하면 된다.
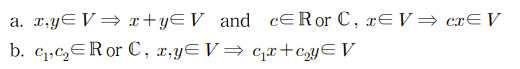위의 조건 a와 b 중 하나만 만족하면 바로 벡터 공간이 된다. 0과 같은 경우에는, 0은 실수 범위에 해당하므로, 0에 어떠한 값을 곱해도 이는 0이 되고, 다시 실수 범위에 해당한다. 즉, 모든 벡터 공간은 0을 항상 포함하게 되는 셈이다. 그럼 어떠한 것들이 벡터 공간에 해당하는지 조금 더 알아보자.
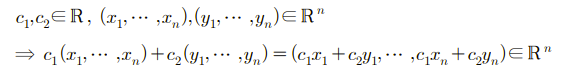지금까지 알고 있는 n차원의 유클리드 공간들은 모두 벡터 공간이다.
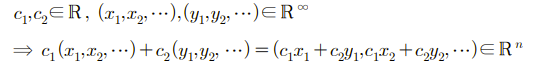무한차원의 유클리드 공간도 벡터 공간이다.
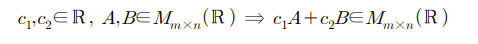우리가 이제부터 해를 구해나갈 행이 m이고 열이 n인 행렬의 집합도 벡터 공간이다.
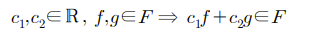특정 구간내에서 정의된 함수들의 집합 또한 벡터 공간이 된다.
위의 조건들만 만족한다면 그 어떠한 공간도 벡터 공간이 될 수 있다. 그리고 벡터 공간 안에 포함된 또 다른 공간이 있다면, 이 또한 벡터 공간이고 우리는 이 공간을 따로 부분 공간(Subspace)라고 할 것이다.
부분 공간(Subspace)이라는 용어가 등장했는데, 부분 집합(Subset)과 잘 구분해야만 한다. 부분 공간은 벡터 공간의 부분 집합일 뿐만 아니라, 위의 조건인 더하기와 실수 곱에 닫혀있어야 한다.
즉, 부분 공간은 부분 집합이면서 더하기와 실수 곱에 닫혀있어야 한다는 조건이 추가로 필요한 것이다.
열 공간(Column Space)
지금부터 벡터 공간들 중에서 가장 중요한 4가지 벡터 공간에 대해서 알아볼 것이다. 그 중 첫번째로 알아 볼 공간은 열 공간(Column Space)이다. 열 공간이란는 이름부터 행렬의 열이 떠오를 것인데, 어느정도는 맞는 이야기이다. 열 공간을 정의해보면, 열 공간이라는 것은 m by n 행렬 A가 있을 때, 이 A의 열 벡터들의 모든 선형 결합(Linear Combination)들을 포함하는 집합이다. A의 열 공간은 m차원 R의 부분 공간이 되고, A의 열 벡터 들이 m차원 R을 생성(Span) 할 때에만 A의 열 공간이 m차원 R이 된다. 우선 열 공간이 벡터 공간이 맞는지 확인해보자.
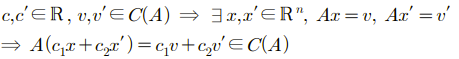더하기와 실수 곱에 대해서 닫혀 있음이 확인이 가능해서 열 공간이 벡터 공간임은 틀림이 없다. 앞으로 열 공간은 C(A)라고 표기할 것이다. 이제 간단하게 예시를 들어보자.
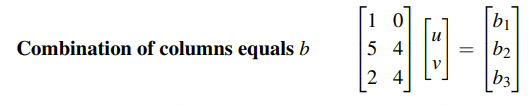위와 같이 Ax = b 행렬식이 존재하고 m과 n의 크기가 다른 경우에(m > n), 흔히 해는 존재하지 않는다. 하지만 우리는 해를 찾아야 하는 경우가 대부분일 것이다.
그래서 Ax = b 가 해를 가지기 위해서는 벡터 b가 A의 열 공간안에 존재해야 한다. 이 조건만 만족하면 우리는 주어진 행렬식을 풀 수가 있다.
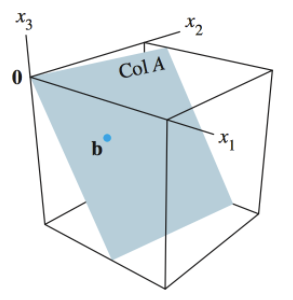즉, 다음과 같이 선형 결합을 했을 때, 벡터 b가 A의 열들의 선형 결합의 형태로 표현이 되어야, b가 열 공간 안에 있을 수 있게 된다.
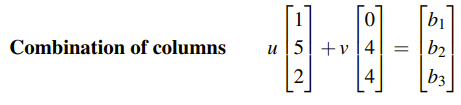
영 공간(Null Space)
두번째로 살펴 볼 공간은 영 공간(Null Space)이다. 열 공간과 같이 이름에서 알 수 있듯이 숫자 0과 관련되 공간일 것임을 알 수 있다. m by n 행렬 A가 주어졌을 때, Ax = 0의 해들을 전부 모은 집합이다. Ax = 0은 어떻게 보면 Ax = b의 특수한 경우이다. 그래서 열 공간과 영 공간을 같이 살펴보는 것이다. A의 영 공간은 n차원 R의 부분 공간이 되고, 열 공간과는 차원 수가 다름을 알아둬야 한다.
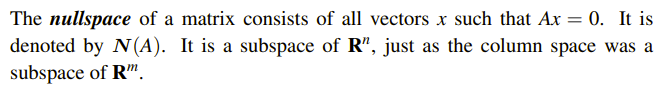열 공간과 마찬가지로 영 공간이 벡터 공간임을 확인해보자.
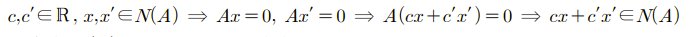영 공간도 더하기와 실수 곱에 닫혀있으므로 벡터 공간이 된다. 그리고 영 공간(Null Space)는 앞으로 N(A)라고 표기할 것이다.
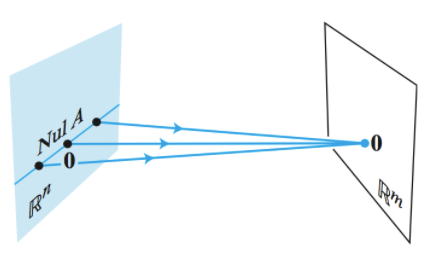영 공간의 예시를 살펴보자.
가장 간단한 경우로 A가 invertible하면, Ax = 0의 해는 오직 0밖에 없으므로 N(A) = {0}이 된다.
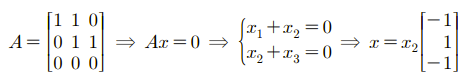위의 예시를 통해서 우리는 A의 영 공간은 (-1, 1, -1)의 상수배임을 구할 수 있다. 이는 곧 직선을 말하게 되고, 다음과 같이 표현할 수 있다.
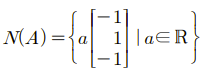조금 더 복잡한 예시를 보자.
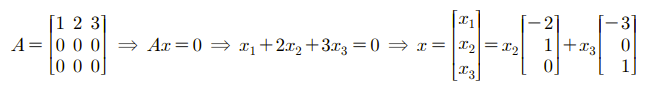이번 예시는 두 벡터의 선형 결합 형태로 되어 있음을 확인할 수 있다. 즉, 이는 공간을 의미하며 다음과 같이 실수 상수를 하나 추가해 표현할 수 있다.
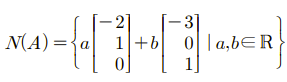
조금 정리를 해보면, 벡터 b는 열 공간(Column Space) 안에 있고, 벡터 x는 영 공간(Null Space)안에 있다. 우리는 앞으로 이 공간들의 차원과 이 공간들을 생성하기 위한 벡터 집합을 잘 계산할 줄 알아야 한다. 그리고 우리는 어떠한 행렬식인 Ax = b가 주어졌을 때, C(A)와 N(A)를 구해야 하며, C(A)는 우변의 벡터 b와의 관계를 잘 살펴보고, N(A)는 Ax = 0일 때 가능한 해의 경우를 잘 살펴봐야 한다.
