Linear Independence or Dependence
벡터들이 서로 linear independent 한지, dependent 한지는 다음의 정의를 보면 알 수 있다.
벡터 공간 V에서 k개의 벡터 v와 상수 c가 있을 때, 벡터 v의 c배의 합이 0인데, 여기서 c가 전부 0이면 linear independent하다 하고, c가 0이 아니면 linear dependent하다고 한다. 추가로 알아야 할 사실은 임의의 벡터 v가 V에 있을 때, v를 c와 다른 v의 곱으로 표현하는 방법이 하나밖에 없다면 이것은 linearly independent와 동치이다.
0 벡터는 linearly dependent하다. c0 = 0을 만족하는 c는 무수히 많은 수가 가능하기 때문이다. 그렇다면 0 벡터가 아닌 벡터는 linearly independent하다. cx = 0을 만족하는 c는 0밖에 없기 때문이다.
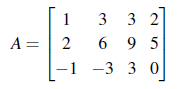위 A의 column들은 linearly dependent하다. 그 이유는 두번째 column이 첫번째 column의 3배이기 때문이다. (-3), 1, 0, 0의 c값들을 column에 곱해서 더하게 되면 0이 된다.
A의 row은 어떨까? A의 row도 또한 linearly dependent하다. 세번째 row는 2번째 row의 2배와 첫번재 row의 (-5)배의 합이다.
이 upper triangular matrix A의 column은 linearly independent하다. 이를 만족하는 조합을 만드는 c는 다음과 같이 0일 때만 가능하다.
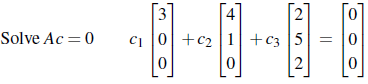지금까지 봤을 때 어떠한 사실을 알 수 있는가.
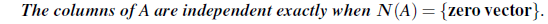A의 column들이 linearly independent하면 Ax = 0의 해는 오직 x = 0뿐이다. 따라서 N(A) = {0}이 되고, 또한 linearly independent의 동치에 의해서 Ax = b를 만족시키는 해 역시 하나뿐이다.
Echelon matrix U의 0이 아닌 행들은 반드시 linealy independent하다. 또한 pivot을 가진 열들도 linearly independent하다. 지금까지 잘 이해해왔다면, 이 사실들이 당연하게 받아들여질 것이다. U뿐만 아니라 row reduced form R도 마찬가지이다.
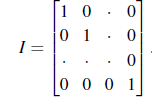n by n의 단위 행렬 I의 열들도 linearly independent하다.
지금까지 여러 예시들을 통해서 linearly independence에 대해서 알아봤다. 생각보다 정의에 임하면 판단이 가능하다. 그래도 아직 어려움이 있다면, 원하는 벡터들을 모아다가 열로 이루어진 새로운 행렬 A를 만들어서 N(A) = {0}인지 알아보면 확실하다.
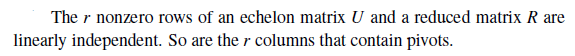U와 R에서 r개의 0이 아닌 row들이 linearly independent하다면, 이 사실로부터 r개의 pivot을 포함하는 column이 존재한다는 것을 알 수 있다.
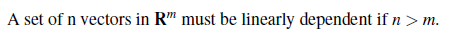m by n 행렬에서 n이 m보다 크면 free variable이 반드시 존재한다. 그렇기 때문에 n > m인 경우에 행렬의 column은 항상 linearly dependent 하다.
Spanning a Subspace
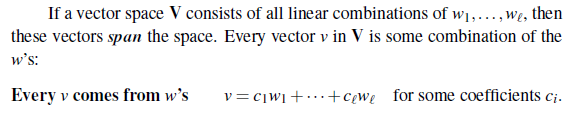Span이라는 말은 위와 같이 조건을 만족하는 벡터들이 어떤 벡터 공간을 형성할 때 사용된다.
예를 들어 a = (1, 0, 0), b = (0, 1, 0), c = (-2, 0, 0)이라는 벡터들이 존재할 때, 이 벡터들은 xy 평면을 span한다. 하지만 a와 b만 있어도 xy 평면을 span하게 된다. 한편 a와 c만 있게 된다면 x축을 span하게 될 것이다.
앞서 우리가 열 공간 C(A)에 대해서 알아봤는데, span의 개념을 도입하면 A의 column들이 열 공간을 span하는 것이다.
Basis for a Subspace
기저(Basis)는 굉장히 중요한 개념이다. 벡터 공간 V가 주어졌을 때, 가장 먼저 확인해야 할 것이기 때문이다. Basis가 V에 있는 모든 벡터들을 대표할 수 있다.
Basis는 위의 두 성질을 만족하면 된다. 벡터들이 linearly independent하면서, 벡터 공간 V를 span하면 된다. 그래서 위의 두 개념을 먼저 살펴본 것이다. 즉, V의 basis인 벡터 v가 존재하게 되면, 모든 벡터를 basis 벡터들의 조합으로 표현이 가능하게 된다. 쉽게 이해하려면 basis는 벡터 공간의 가장 기본 뼈대로 생각하고 여러가지 조합으로 해당 공간에 여러 벡터를 생성한다고 생각하면 된다. 다음의 예시를 보자.
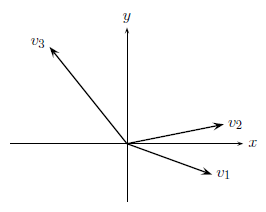
위는 xy평면으로 2차원이다. v1은 그 자체로 linearly independent 하지만, 이 벡터만으로 2차원을 span할 수 없다. 그렇다면 벡터가 3개이면 어떨까? 이 경우에는 확실하게 2차원 평면을 span할 수 있지만, linearly independent하지 못하다. 3개 중 2개로 나머지 1개를 표현할 수 있기 때문이다. 그래서 이 경우에는 2개의 벡터만을 가지고 basis를 이룰 수 있다. 2개의 벡터로는 2차원을 span하면서 linearly independent하기 때문이다. 그리고 중요한 사실로 알아둬야하는 부분은 하나의 벡터 공간이 반드시 한가지 경우의 basis를 가지는 것은 아니다. Basis는 unique하지 않고 여러 경우가 존재할 수 있다.
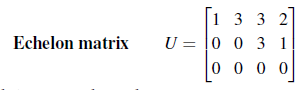이 경우는 어떠한가? Echelon matrix U는 4개의 column으로 구성되어 있다. 앞서 말했듯이 U의 column들은 열 공간 C(U)를 span한다. 하지만, column들이 linearly dependent하기 때문에 basis는 될 수 없다. 여기서 pivot이 있는 첫번째와 세번째 column은 linearly independent하고, C(U)를 span 하기 때문에 첫번째와 세번째 column만 basis가 된다.
즉, 어떠한 행렬에서 열들이 열 공간을 span할 때, 만약 이들이 linearly independent 하다면 이들은 열 공간의 basis가 되는 것이다.
Dimension of a Subspace
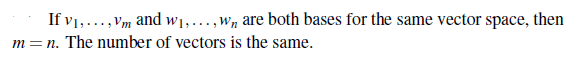벡터 공간 V에서 basis를 2개 알고 있다면, 이 basis의 개수는 동일할 것이다. Basis의 개수는 어떻게 있어도 개수가 같아야 하며, 이 basis의 개수를 차원(Dimension)이라고 하고, 기호로 dim(V) 라고 표기한다.
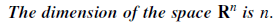우리가 흔히 실수 공간을 자주 표기하는데, 이 때 R의 지수에 있는 숫자가 그 공간의 dimension을 의미한다. 이는 곧 basis가 n개임을 말한다.
V가 linearly independent하게 벡터 v를 선택했을 때, 만약에 이 v들만으로 V를 span하지 못한다면, 이들과 linearly independent하게 새로운 벡터들을 추가해서 basis를 만들 수 있다. 반대로, 벡터 v들이 V를 span하지만 linearly dependent하다면, 벡터를 하나씩 제외하면서 basis를 만들 수 있다.
