우리는 기존의 invertible한 정사각행렬에서 유일한 해의 존재에 대해서 알아봤다. Gaussian Elimination을 사용했는데, 이제는 m by n 행렬이 주어져도 마찬가지로 Gaussian Elimination을 사용해서 해를 구할 것이다. 하지만 이 경우에 m과 n의 크기가 같은 정사각행렬이 아닌 경우에 Upper Triangula Matrix는 만들어지지 않고, Back Substitution을 하려고 해도 정해진 값이 없어 해를 구하다보면 아예 존재하지 않거나 무수히 많을 것이다. 하지만 이런 경우 이제 벡터 공간을 알았기 때문에 벡터 공간을 이용해서 좀 더 구체적으로 표현할 수 있게 되었다.
Echelon Form U
바로 간단한 예시로부터 Echelon Form이 무엇인지 알아볼 것이다.
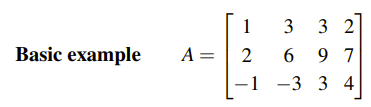위와 같이 평범한 4 by 3 행렬 A가 있다. 첫번째 피벗은 1로 0이 아닌 것을 볼 수 있고, 두번째 피벗을 찾기 위해서 Gaussian Elimination을 진행했다.
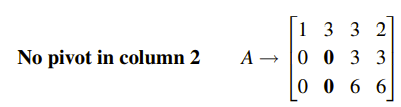그런데 진행해본 결과, 두번째 피벗이 0이 나와버렸다. 그래서 행 교환을 하려고 하니 아래도 0이 생겨 두번째 열에 대한 피벗이 없음을 알았다. 이 경우에는 다음 행으로 넘어가 0이 아닌 숫자가 오면 그 숫자를 피벗으로 생각할 것이다. 아무래도 정사각행렬이 아니다보니 열의 개수가 많아지면, 특정 열은 피벗이 없을 수 밖에 없다. 그래서 두번째 피벗은 3이 된다. 다시 Gaussian Elimination을 진행하면 다음과 같이 나온다.
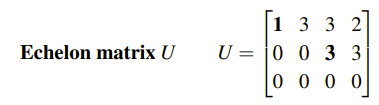마지막 행까지 소거법이 끝나고 나면 남은 행렬을 가지고 Upper Triangular Matrix과 같은 기호 U를 사용하고, 우리는 이를 Echelon Form이라고 할 것이다. 위의 예시에서는 피벗이 1과 3으로 2개뿐이었다. 이처럼 피벗의 개수는 행과 열의 개수와 굳이 똑같을 필요가 없다. 정사각행렬의 경우는 똑같아야 하지만, 일반적으로 행과 열의 개수가 다를 때는 0이 아닌 숫자에만 주목해서 피벗으로 설정하면 된다. 이를 더 확장해보면 Echelon Form은 다음과 같이 계단 모양의 꼴이 나오게 될 것이다.
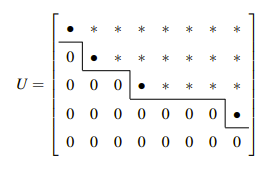위의 4 by 3 행렬 U에서 기본 행렬(Elementary Matrix)까지 이용하게 되면 A = LU 혹은 A = LDU Factorization이 가능하게 된다.
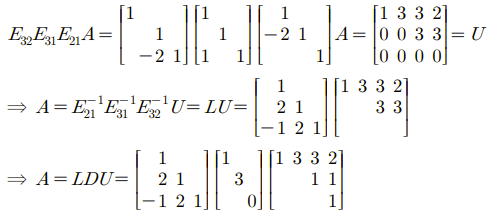
Row Reduced Form R
A로부터 Echelon Form U까지 잘 만들었다. 하지만 우리는 U를 더 간단하게 만들고 싶다. 그래서 U에서 피벗이 존재하는 열의 윗부분까지 전부 0으로 만들고, 각각의 행을 피벗으로 나누어 피벗이 전부 1인 상태로 만들고 싶다. 우리는 다음과 같이 추가로 소거법을 이용해서 만든 형태를 Row Reduced Form이라 할 것이고, R이라고 표기할 것이다.
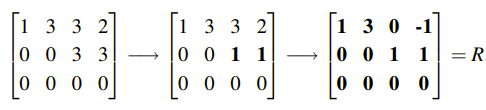이렇게 하는 이유는 처음에 방정식을 Column Form과 Matrix Notation으로 바꾼 이유와 같다. 데이터의 개수가 많아질수록 계산이 복잡해지는데, 이러한 과정을 하는 자체도 계산의 효율성을 위해서 더욱 간단한 형태로 바꾸기 위해서다.
Pivot Variables and Free Variables
우리는 이제 Ax = 0을 풀고 싶다. 여기서 알아야 할 사실은 Ax = 0의 해는 Ux = 0, Rx = 0의 해와 같다는 것이다. 즉, 소거법을 이용해 A를 간단하게 바꿨더라도 해는 변함이 없다는 것이다. 그래서 우리가 지금까지 행렬을 변형시킨 것이다.
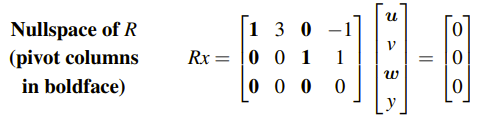우리는 미지수 u, v, w, y를 2개의 그룹으로 나눌 수 있다. 하나의 그룹은 피벗이 존재하는 열에 해당하는 Pivot Variable로 위의 경우에는 u와 w가 여기에 해당한다. 그리고 피벗이 존재하지 않는 열에 해당하는 v와 y는 Free Variable에 해당하게 된다. 위의 식을 풀어서 잘 정리하면 다음과 같이 Pivot Variable에 해당하는 U와 w에 대해서 정리할 수 있다. 즉, Pivot variable들을 Free Variable들에 관한 식으로 표현할 수 있다.
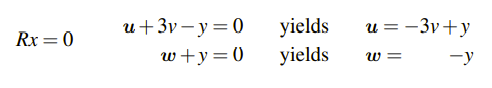그리고 u와 v를 정리한 식을 대입하면 다음과 같이 벡터의 선형 결합 형태로 해를 적을 수 있다. 즉, Ax = 0의 해를 모아 놓은 벡터 공간 N(A)를 찾아낸 것이다.
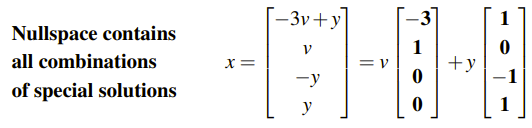이 N(A)에서 특정한 해의 형태를 찾을 수 있다.
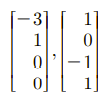위의 벡터들은 N(A)에서 계수를 1로 생각했을 때, 특정한 경우로 보고 이를 우리는 Special Solution이라고 할 것이다. 또한 아래와 같이 Sepcial Solution들을 열로 취하는 행렬을 Nullspace Matrix라고 할 것이다.
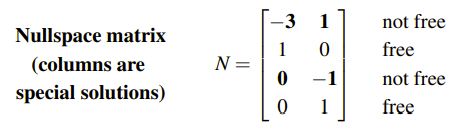Free Variable들은 오직 1과 0의 값만 가지는 것을 알 수 있다. 그래서 우리는 Pivot Variable이 무엇인지 찾게 되면, 이는 곧 해를 구할 때 중요한 단서가 되기 때문에 소거법을 잘 해서 찾는 것이 중요하다.
그리고 추가로 재미있는 사실을 살펴보면 우리는 사실 U까지만 구해도 N(A)를 찾을 수 있다. 그런데 왜 굳이 R까지 구하는 것일까? 물론 앞에서 말한 효율성과 편리함 때문일 것이다. 그리고 이는 R의 구조와 N(A)와의 연관성을 보면 흥미로울 것이다.
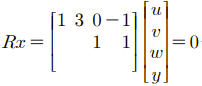다시 위의 식을 잘 보면서 N(A)를 다시 한번 보고 오자. 놀랍게도 구조가 거의 똑같은 것을 알 수 있다.
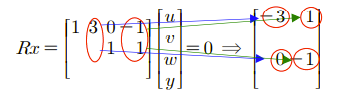Pivot을 가지고 있지 않은 두번째 열과 네번째 열의 값들을 부호를 바꿔서 N(A)의 Pivot Variable 자리에 쓰면 된다.
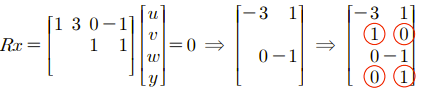그리고 나머지 자리에는 identity가 오도록 1과 0을 적으면 굳이 계산하지 않아도 N(A)를 찾을 수 있다.
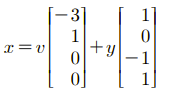추가로 Free Variable들과 짝을 지어 적으면 Nullspace Solution이 구해졌다. 여기까지는 굳이 알지 않아도 크게 상관은 없다.
지금 우리는 m by n 행렬 A에서 n > m 인 경우를 다뤄봤다. 이 경우가 가장 많이 다뤄질 것이기에 중요한데, 이 경우라면 미지수의 개수가 n개이지만, 피벗의 개수는 많아봐야 행의 수인 m을 넘지 못한다. 그래서 무조건 Free Variable이 적어도 n - m 개가 생기고 이에 따라 Special Solution의 개수도 n - m 개가 생긴다. 결국 Ax = 0의 해는 항상 무수히 많다.
Solve Ax = b, Ux = c, Rx = d
이번에는 Ax = b 인 경우에 어떻게 풀 것인지에 대해서 알아보고자 한다. 우변이 0인 경우는 계산이 나름 깔끔했다. 하지만 이제부터는 조금씩 복잡해지는 경우도 나올 것이기에 계산 실수를 조심해서 해야할 필요가 있다. 다음의 예시를 보자.
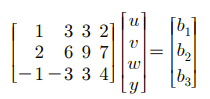이전의 열 공간에 대해서 볼 때, Ax = b가 해를 가지기 위해서는 b가 C(A)에 포함되어야 한다고 했다.
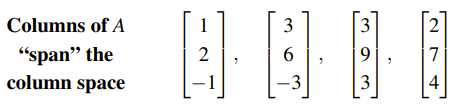하지만 지금 상태로는 파악하기 힘들다. 그렇다면 다음 단계로 넘어갈 텐데, A를 우선 U로 만들어보면 다음과 같이 나오고, 여기서 b도 계산을 통해서 새로운 c로 바뀌게 되었다.
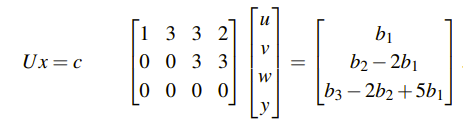아직도 위의 식이 사실 해를 가지는지 명확하게 알 수는 없다. 하지만 위의 식으로부터 우변의 세번째 항이 0이 되어야 한다는 사실은 알 수 있다. 만약 세번째 항이 0이 아니라면, 위의 식은 이뤄질 수 없다. 하지만 이 사실을 알았더라도, 아직 미지수는 많이 존재한다. 일단은 그래도 이 식으로 부터 b = (1, 5, 5)라는 경우를 찾고, 이를 대입해서 문제를 다시 살펴보도록 하자.
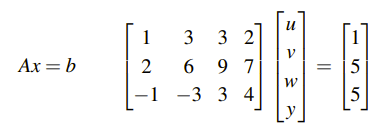
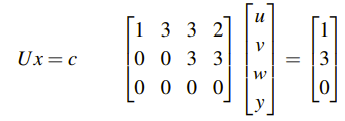일단 하나의 경우를 대입했고, 이를 통해서 다음과 같이 나오게 된다.
이전과 마찬가지로 연립 방정식을 만든 뒤에 Pivot Variable들을 Free Variable들로 표현했다. 그래서 우리는 해를 다음과 같이 찾을 수 있게 되었다.
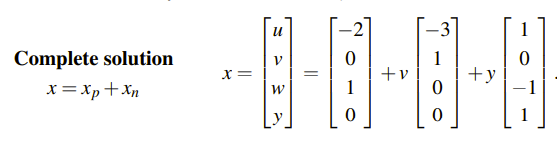우리가 임의로 찾은 것은 Ax = b의 특수한 경우인 Ax = 0의 해이다. 이를 이용해서 문제를 풀어간 것이고, 우리는 위에서 Free Variable이 붙지 않은 부분을 Particular Solution이라고 할 것이다. 이는 Free Variable이 전부 0일 때의 해이고, 해석해보면 Ax = b의 해들을 모아 놓은 집합인 N(A)를 Particular Solution만큼 평행이동 시킨 것으로 해석할 수 있다.
추가로 Ax = b 에서 U를 R로 변형했을 때, 무엇이 더 효율적인지 알아볼 것이다.
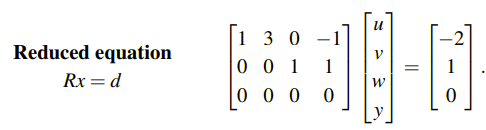이때도 d = (-2, 1, 0)을 이용하면 Particular Solution을 쉽게 구할 수 있다. Pivot이 있는 행과 같은 위치에 있는 숫자 (-2)와 1을 Pivot Variable 자리에 놓고, Free Variable 자리에 0을 채우면 다음과 같이 Particular Solution을 찾을 수 있다.
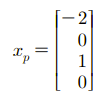
지금까지 배운 내용들을 기반으로 피벗이 얼마나 중요한 역할을 할 수 있는지 볼 수 있다. Pivot Variable의 개수를 r이라 한다면, 우리는 피벗의 개수를 앞으로 rank라고 하고 rank(A) = r이라고 적을 것이다. 이러면 자연스럽게 Free Variable의 개수는 n - r 개가 된다. 이 rank의 개념은 뒤에 자주 등장하므로 피벗의 중요성과 그 개수를 rank라고 한다는 사실을 기억해두면 된다.
