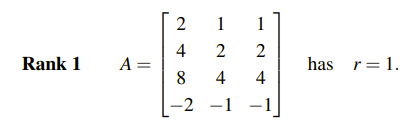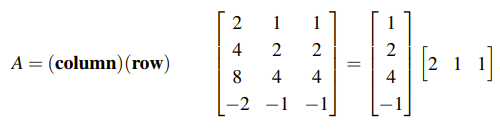이전에 Column space와 Null space에 대해서 알아봤다. 이번에는 이 둘을 포함하여 총 4가지 중요한 벡터 공간들을 살펴볼 것이다. 특히 basis와 dimension에 주목해서 공간들의 특징을 알아볼 것이다.
A의 행은 A를 전치 행렬 한 것의 열이 되는 사실을 알아야 한다. 전치 행렬이 무엇인지 알고 있다면, 행과 열이 바뀌는 것 정도는 쉽게 알 수 있을 것이다. 다음 예시를 한번 살펴보자.
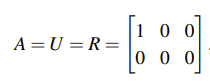Column space는 열들이 span한 공간이기에 dimension이 2일 것이고, 아래에서 다룰 내용이지만, row space는 이름만 봐도 행들이 span한 공간이라는 것을 유추할 수 있을 것이다. 그렇기에 dimension은 3일 것이다.
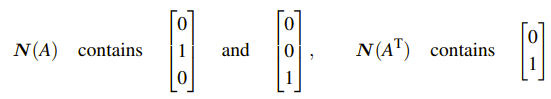그래서 N(A)를 구하면 Ax = 0이 되는 x만 찾으면 되기 때문에, 위와 같이 찾을 수 있고, 오른쪽에는 이 또한 아래서 배울 내용이지만, 미리 살펴보면 A의 전치 행렬의 null space를 구하는 것으로, 이는 left null space라고 한다. 그리고 이들의 dimension이 다른 것에 주목할 필요가 있다. A를 transpose시킨 후에 x를 곱하게 되면 x는 자연스럽게 기존 A의 행의 dimension과 같아지기에, left null space의 dimension 또한 이와 같게 되는 것이다.
앞으로 행렬 A는 m by n으로 간주하고 설명할 것이다
Row Space
어떤 행렬 A가 주어졌을 때, row space는 A의 행들이 span하여 만든 벡터 공간이다. A의 행은 n차원의 벡터이기 때문에 row space는 n차원 공간의 부분 공간이 된다.
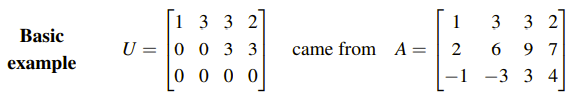위의 예시를 통해서 알아가보자. Echelon form인 U로 바꾸더라도 row space는 변하지 않는다. A에서 모든 행들이 0이 아니기 때문에 어느 행이 중요한 행인지 알기 어렵지만, U에서는 0이 아닌 행들이 명확해서 basis를 찾기가 쉽다. U에서 0이 아닌 행들은 linearly independent하고 row space를 span하는 bais이면서, 이는 또한 A를 span하는 basis가 된다. Row reduced form R에서도 마찬가지이다. 그리고 이 행들만이 pivot을 가지고 있기에 dimension은 r이 된다. 그리고 row space는 다음과 같이 표기할 수 있다.
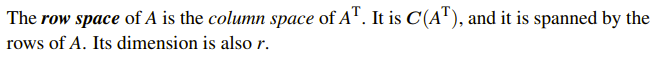
Null Space
Null space는 이전에 보았듯이, Ax = 0의 해들을 모아놓은 공간이다. 해는 n차원 벡터이기 때문에 null space는 n차원 공간의 부분 공간이다. 그리고 Ax = 0, Ux = 0, Rx = 0의 해가 모두 같기 때문에 N(A) = N(U) = N(R)이 된다.
Ax = 0의 해는 free variable과 special solution들의 linear combination으로 이루어져 있다. Special solution들이 Linearly independent하고, 이들이 N(A)를 span하기 때문에, 이들이 N(A)의 basis가 된다. 다음의 벡터들이 위의 예시 A의 null space를 span하는 basis들이다.
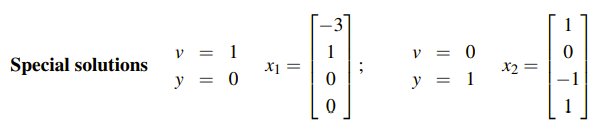그렇다면 N(A)의 dimension은 어떻게 알 수 있을까.
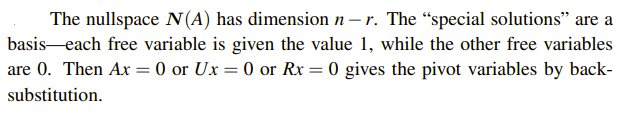Special solution의 개수는 free variable들의 개수와 같으므로, N(A)의 dimension은 n - r이 된다. 다음의 예시를 통해서 살펴보자.
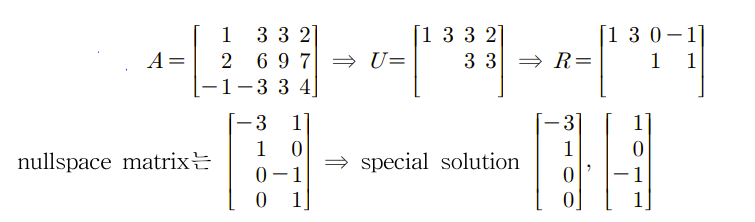우리는 basis의 개수가 곧 dimension임을 알고 있다. 위의 예시에서 special solution이 basis가 되는 것도 알고 있다. 그런데 special solution은 pivot이 아닌 free variable의 수와 같음을 또한 알고 있다. 그렇기 때문에 n에서 pivot의 개수인 rank를 빼주게 되면 바로 dimension이 되는 것을 알 수 있다.
Column Space
Column space도 이전에 보았듯이, A의 열들이 span 한 공간을 말한다. A의 열들은 m차원 벡터들이기 때문에 column space는 m차원 공간의 부분 공간이다. 위에서 Gaussian Elimination을 하더라도 row space는 변하지 않았다. 하지만 column space는 변하기 때문에 U와 R과는 상관없이 A만을 가지고 찾아야 한다. 하지만 basis를 찾기 위해서는 U와 R을 만들 필요가 있다. 단지, row space에서는 U와 R의 행들이 A도 span하기에 basis가 되지만, column space에서는 pivot이 있는 열들을 찾고, 단지 그 위치 정보만 제공해 줄 수 있다. 이렇게 찾은 pivot이 있는 열의 위치를 기억해서 A의 열을 보면 그 위치에 있는 열들이 basis가 되는 것이다. 쉽게 말하면, U에서 pivot을 가지는 열들과 같은 위치에 있는 A의 열들이 C(A)의 basis가 된다.
U에서 pivot을 가지는 열과 같은 위치에 있는 A의 열의 개수는 rank(A)로 r이므로, column space의 dimension은 r이 된다. 예시를 통해 살펴보자.
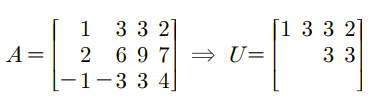여기서 C(U)가 xy 평면이 되지만 C(A)의 열들은 xy 평면에 존재하지 않는다. 그렇기 때문에 row space와 달리 column space에선 U를 통해서 basis를 바로 찾으면 안되는 것이다.
Left Null Space
갑자기 왜 이런 공간을 배우는지 의문을 가질 수 있다. 위의 3가지 공간은 이름 그대로 확실한 특징을 가지는데 반해 left null space는 감이 잘 오지 않을 것이다. 일단 null space이기 때문에 어떠한 행렬의 해들의 공간을 찾을 것은 확실해 보인다. 바로 우리는 여기서 A의 전치행렬의 null space를 구할 것이다. 이름이 left null space인 이유는 다음과 같이 x가 A의 왼쪽에 곱해져 있는 모양이기 때문이다.
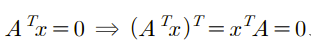전치 행렬 A의 해는 A의 해가 n차원 벡터였기 때문에, m차원 벡터가 된다. 그래서 left null space는 m차원 공간의 부분 공간이다. Left null space의 basis는 null space의 basis와 똑같이 구하면 된다. 이제 중요한 것은 dimension이 null space에서는 n에서 rank를 뺏지만, left null space에서는 m에서 rank를 뺀 m - r이 된다.
간단하게 정리해보면 다음과 같다.
그리고 추가로 basis를 구하는 방법을 정리해보면 다음과 같다
- Column space : U에서 pivot을 가지는 열들과 같은 위치에 있는 A의 열들
- Null space : A의 special solution 벡터들
- Row space : U에서 0이 아닌 행들
- Left null space : 전치 행렬 A의 special solution 벡터들
정리는 해보았지만, basis는 철저하게 정의에 의해서 정해진 벡터들이므로, 원리와 정의를 잘 알고 있는 것이 중요하다.
Existence of Inverses
m by n 행렬 A가 주어지면, A의 rank r은 항상 m, n보다 작거나 같게 된다. 이때 r이 최대한으로 크면 이를 full-rank라 하고, 이 경우에는 left inverse나 right inverse가 존재한다. 그럼 어떠한 경우에 inverse가 존재하는지 하나씩 알아보자.
정사각 행렬인 경우에는 r이 m, n과 동시에 같은 경우가 존재할 것이다. 그러면 위의 두가지 성질을 모두 만족하여 left inverse와 right inverse를 모두 가지게 된다.
Matrices of Rank 1
Rank가 1인 행렬 A는 linearly independent한 열이 하나이고, linearly independent한 행도 하나이다. 즉, 모든 열이 하나의 열의 상수배이고, 모든 행이 하나의 행의 상수배인 셈이다. 이 경우에는 다음과 같이 하나의 행과 열의 곱으로 표기할 수 있다.
