Transformation
보통 수학을 공부하면서 한 종류의 집합 개념을 배우게 되면, 그 다음에는 이들 사이의 함수나 중요한 특성들에 대해서 배우게 된다. 지금까지 벡터 공간들에 대해서 계속 살펴보았는데, 이번에는 벡터 공간 사이의 함수들 중에서 특별한 특성을 가진 함수인 transformation에 대해서 살펴볼 것이다.
Linear Transformation의 정의는 다음과 같다. 집합 V와 W를 벡터 공간이라고 할 때, 벡터 공간 V로부터 벡터 공간 W로의 함수 T : V -> W가 V의 모든 원소 a, b에 대해서 T(ca + b) = c(T(a)) + T(b)이면, 어떤 함수 T를 V를 W에 대한 linear transformation이라고 한다.
여기서 주의해야 하는 부부은 T(ca + b)는 V에서 정의가 된 것이고, c(T(a)) + T(b)는 W에서 정의된 것이다. 몇가지 예를 보면서 알아보자.
1. Zero transformation : 함수 T가 모든 V의 원소에 대해서 항상 W의 0 벡터를 대응시키면, T(ca + b) = 0 = c0 + 0 = c(T(a)) = T(b)가 성립하므로 linear transformation이 된다.
2. Identity map : 함수 I가 V -> V이고, 벡터 b에 대해서 Iv = v인 함수를 identity map이라고 부르는데, 이 또한 linear transformation이다.
3. Line in plane : 함수 f가 R -> R이고, f(x) = kx와 같이 원점을 지나는 직선이면, 이는 linear transformation이다. 만약 함수가 직선이 아니라면 linear transformation이 아니게 되고, 또한 직선이라고 하더라도 원점을 지나지 않으면 linear transformation이 아니다.
직선이 원점을 지난다는 것은 0에 대해서 함수 값이 0이라는 것을 의미하는데, 이는 0 벡터의 함수 값은 0 벡터가 된다는 것이다. 이는 T(a) = T(a + 0) = T(a) + T(0) 이므로 T0 = 0이 된다. 앞의 0 벡터는 V에 속하고, 뒤의 0 벡터는 W에 속하는 것에 유의하면 된다. 그리고 V에서의 linear combination에 대한 linear transforamtion은 W에서의 linear combination이 된다.
4. Differentiation : 미분이 가능한 함수들의 집합 V와 연속인 함수들의 집합 W는 벡터 공간이라고 할 때, T를 V -> W로 정의할 것이다. 이때 미분 가능한 함수 f에 대해서 f에 T를 곱하면 f가 x에 대해서 미분이 된다면, 미분의 성질에 의해서 다음과 같아지므로, T는 정의에 의해 linear transformation이 된다.
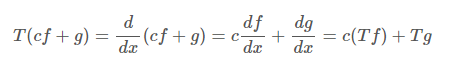
간단하게 linear transformation의 정의에 입각해서 몇가지 예시들을 살펴보았다. 우리는 이제 이 함수 T를 행렬에 대해서 어떻게 나타낼 수 있는지 볼 것이다.
Transformations Represented by Matrices
임의의 linear transformation 함수 T가 주어지면, 이와 관련해서 행렬로 만들 수 있을까? 이 질문에 대한 대답은 "yes"이다. Linear transforamtion의 집합 역시 벡터 공간이므로, 벡터 공간을 span하는 basis를 잘 이용하여 행렬로 표현이 가능할 것이다. 우리는 basis에 주목하게 되면 쉽게 가능할 것이다. Basis라는 것이 벡터 공간의 기반이 되기 때문에 벡터 공간 V와 W가 주어졌을 때, V의 basis들이 어떤 T에 의해서 W의 어디로만 보내지는지 알게 되면 V의 모든 벡터가 어디로 보내지는지 알 수 있게 된다. 우리가 알고리즘을 만들 때 경우를 잘 생각해서 만들어 놓으면, 어떠한 값이 입력값으로 들어와도 출력값이 잘 나올 것이다. 이와 유사하게 생각해도 좋을 것이다. Basis를 이용해서 다른 벡터들도 표현할 수 있다는 것이다.
그렇다면 벡터 공간 V의 벡터들을 v라고 한다면, 우리는 V 내에서 어떠한 벡터도 다른 v들과 상수 c들의 linear combination으로 표현할 수 있다.
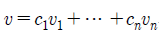그리고 linear transforamtion 함수 T에 의해서 다음과 같이 표현할 수 있다.
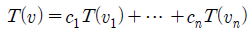이 이야기는 T에 의해서 V의 벡터 v들이 W로 보내지게 된다는 것은 특정 벡터 v를 W의 벡터들인 w와 상수의 linear combination으로 표현이 가능하다는 이야기다.
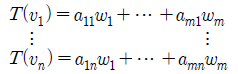위의 식들을 통해서 matrix form으로 표현을 바꾸게 되면 우리는 다음과 같이 A를 만들 수 있고, 이는 T와 관련된 행렬로 표현이 된 셈이다.
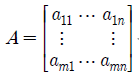그럼 이제 간단한 예제를 보도록 하자. 앞서 미분도 linear transforamtion의 일종이라고 했다. 우리가 직선은 1차식으로, 평면은 2차식으로 보통 표현하는데, 이때 쉽게 생각해볼 수 있는 것이 xy 평면은 x축과 y축이 대표적인 basis임을 알 수 있다. 즉, (1, 0)과 (0, 1)만으로 xy 평면을 span하게 되는 것이다. 이러한 느낌으로 3차원 다항식에서의 대표적인 basis로 다음과 같다.
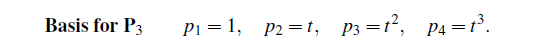물론 이 basis는 unique한 것은 아니다. 하지만 굳이 복잡하게 basis를 결정할 필요가 없다. 이제 이 basis들을 t에 대해서 미분하면 다음과 같고 우리는 linear transformation A를 찾을 것이다.
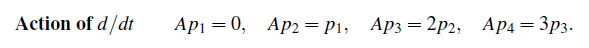위의 결과는 다음과 같은 과정을 통해서 표현할 수 있으며, A도 위의 계수들을 이용해서 만들 수가 있다.
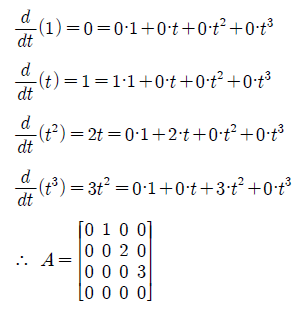
미분을 식을 통해서 보면, 이 행렬이 잘 작성된 것인지 눈으로 확인이 가능하다.
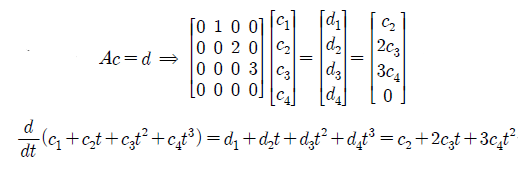지금까지 쉬운 예시인 미분을 통해서 어떻게 linear transformation을 행렬로 표현하는지 알아보았다. 미분도 표현이 가능하다면, 적분도 표현이 가능할 것이다. 설명은 하지 않겠지만, 다음과 같이 똑같은 메커니즘에 의해서 linear transformation을 찾을 수 있다.
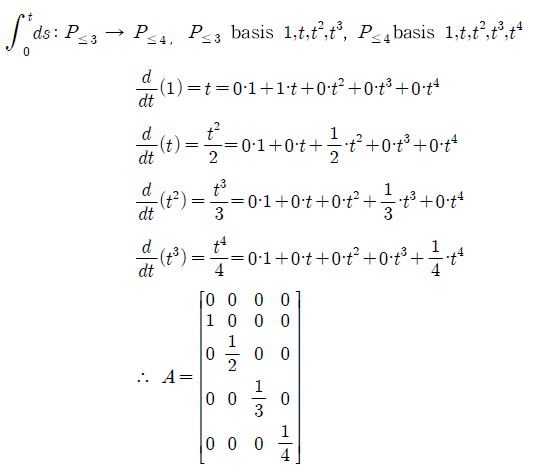또한 다음과 같이 linear transforamtion B를 만들 수 있다.
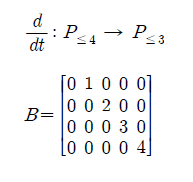미분과 적분을 같이 배우는 이유는 이 둘은 서로 역관계이기 때문이다. 그렇다면, 위의 A와 B를 통해서 어떠한 사실을 알게 되었는가? 바로 B와 A를 곱하게 되면 단위 행렬 I가 만들어지는 것이다(BA = I). 즉, B는 A의 left inverse로, linear transformation의 합성 함수를 표현하면 그와 관련된 matrix의 곱과 같게 된다.
Rotations Q
Rotation은 말 그대로 행렬을 회전시키고 싶은 것이다. 다음과 같이 우리가 벡터들을 특정 각도 θ만큼 회전을 시키고 싶을 때 필요한 linear transforamtion matrix를 알고 싶다.
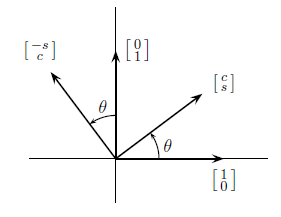벡터 (1, 0)은 (cosθ, sinθ)로, 벡터 (0, 1)은 (-sinθ, cosθ)로 회전하는 것을 알 수 있다. 왜 이러는지는 고등학교를 다니면서 삼각 함수를 배웠다면 이해가 될 것이다.
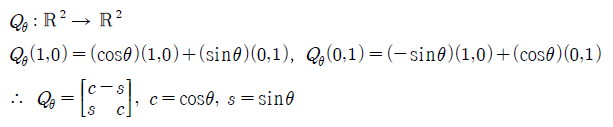더불어 알아두면 좋은 내용으로, linear transformation이 어떻게 되는지 알게 되면, 이와 관련된 행렬의 역행렬이나 곱들을 쉽게 구할 수 있다.
1. inverse : rotation backward through θ
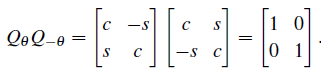앞서 Gauss-Jordan 방법을 통해서 inverse를 구할 수 있지만, 삼각함수의 경우 성질을 이용하면 굉장히 쉽게 찾을 수 있다. cosθ와 sinθ를 각각 제곱해서 더해주면 1이 되는 것을 이용하면 간단해진다. 식을 외우려면 θ에 (-θ)를 넣으면 된다. sin함수는 부호가 밖으로 나오게 되므로, sin의 원소만 부호를 바꿔주면 된다.
2. square : rotation through a double angle
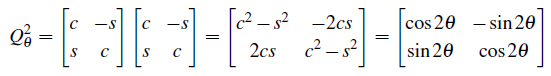
3. product : rotation through x then φ
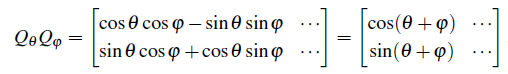이 경우는 inverse와 square를 모두 포함하는 경우이다. φ가 (-θ)라면 inverse이고, φ가 θ라면 square인 셈이다.
Projections P
Projection P는 우리가 어딘가로 투영, 정사영 시키고 싶을 때 사용하는 행렬이다.
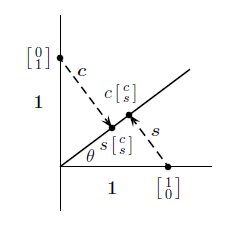y = (tanθ)x라는 직선으로 정사영시키는 transformation은 다음과 같이 구할 수 있다.
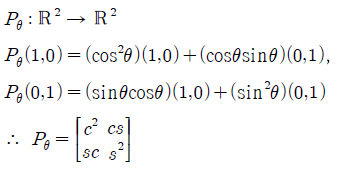재미있는 사실은 P는 invertible하지 않으면서, symmetric하다. P가 역행렬을 가지는 경우는 P가 n by n의 정사각 행렬이며 역행렬이 존재해야하는데, 이는 결국 n차원 공간에서 n차원의 공간으로 투영시키는 셈인데, 결국에는 단위 행렬 I를 의미하게 되어 결과적으로 투영을 시키더라도 아무 일도 일어나지 않는다. 그래서 P는 invertible하지 않다.
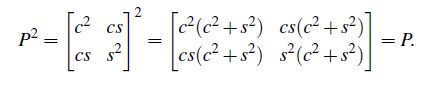그리고 제곱하게 되면 다시 자기 자신이 된다. 이 말은 투영을 한 결과를 다시 투영하게 된다면 그대로 가리키는 벡터가 된다는 소리이고, 이는 몇번을 하더라도 그대로일 것이다.
P가 symmetirc이며, 제곱해도 같음은 다음과 같이 간단하게 증명을 해볼 수 있다.
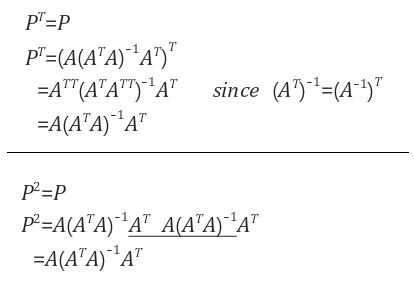
Reflections H
Reflection H는 우리가 어딘가를 기준으로 대칭 이동 시키고 싶을 때 사용하는 행렬이다.
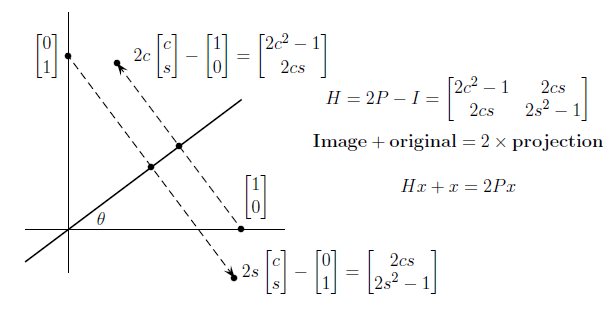y = (tanθ)x라는 직선을 기준으로 대칭 이동시키는 transformation은 다음과 같이 구할 수 있다.
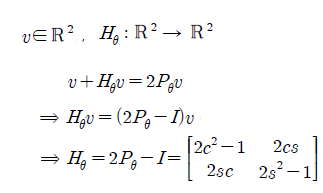H의 inverse는 H 그대로며, 제곱을 하게 되면 단위 행렬 I가 된다. 이는 자연스럽다. 어느 dimension이든, reflection을 2번 하게 되면 다시 시작 지점으로 돌아올 것이다. 즉, 이 행렬을 2번 곱한다는 것은 대칭시킨 결과를 다시 대칭 시킨다는 것인데, 결국 원래 자리로 돌아오게 된다. 같은 행렬의 제곱이 I일 경우에, 이 행렬의 역행렬은 자기 자신이 될 것이다. AB = BA = I라면, B는 A의 역행렬이 되는데, reflection같은 경우 B도 A여야 A의 제곱이 I가 되므로, 결론적으로 inverse는 자기 자신이 된다.
