Introduction
선형 방정식을 풀어야 할 때, 가장 단순하면서 가장 중요한 경우가 바로 미지수(Unknown)와 방정식(Equation)의 수가 같은 경우이다. n개의 방정식과 미지수가 있을 때, n = 2라는 가장 간단한 경우부터 생각해볼 것이다.
여기서 미지수는 x와 y일텐데, 우리는 2가지 방법으로 이 방정식들을 풀어보고자 한다.
1. 소거법(Elimination) : 주어진 방정식들의 계수를 맞춰가면서 뺄셈 연산을 해가는 방법이다. 
그리고 1개의 미지수가 결정이 되면, 이를 역으로 대입해서 다른 미지수들을 찾아가는 방법이다. 이 과정은 후방 대입(Back-substitution)이라고 한다.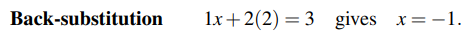 
2. 행렬식(Determinants) : 주어진 방정식들의 계수를 행렬식으로 변환해서 미지수를 구하는 방법이다.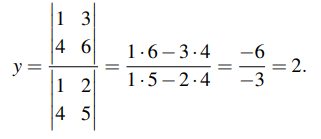 
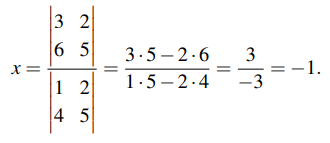
Gaussian Elimination
위와 같이 n = 2인 쉬운 경우에 대해서는 접근하기 좋은 방법이지만, 만약에 n이 무수히 커져서 n = 1000인 경우에는 어떻게 할 것인가? 1000개의 방정식과 미지수를 다 적어가면서 풀어갈 것인가? 물론 노력하면 풀 수는 있지만, 효율적이지는 못하다. 그래서 새로운 방법으로 Gaussian Elimination을 사용하고자 한다. 이 알고리즘은 크기가 큰 방정식들을 해결할 때 유용하게 사용이 될 수 있다.
Gaussian Elimination은 연립일차방정식을 풀이하는 알고리즘으로, 풀어가는 과정 속에서 일부 미지수가 차츰 소거되어 결국 남은 미지수에 대한 선형 결합으로 표현되면서 풀이가 완성된다. 이 방법은 보통 행렬을 사용하며, 이후 행렬식과 역행렬의 계산에도 응용된다. 앞으로 등장하는 다양한 풀이 방법을 통해서 Gaussian Elimination을 차근차근 설명해보고자 할 것이다.
