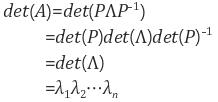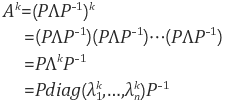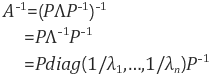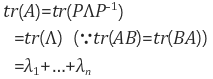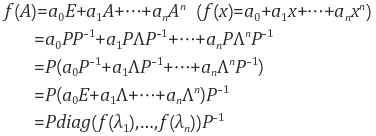이 글은 https://www.deeplearningbook.org/ 책을 정리한 글이다. 연세대학교 인공지능 대학원에서 입학 시험 가이드로 주었으며 딥러닝을 위한 기초 공부를 위해 도움이 될 거라고 생각한다.
Notation
Introduction
딥러닝의 발전 과정에 대해서 내용을 담고 있다.
Linear Algebra
Sclars, Vectors, Matrices and Tensors
스칼라, 벡터, 행렬, 텐서에 대한 설명과 표현하는 방식에 대해서 알려준다.
Transpose
main diagonal을 중심으로 뒤집기
행렬의 연산
기본적인 합연산에 대해서 broadcasting을 할 수 있다.
행렬의 곱연산에는 dot product와 element-wise product가 있다.
전치의 분배는 다음과 같다.
Identity and Inverse Matrices
Ax = b에서 해를 구하는데 사용될 수 있는 역행렬
하지만 역행렬은 근사하는 해를 구하는데 이용될수가 없지
Linear Dependence and Span
Ax = b에서 x라는 해가 가질 수 있는 가능성은 세 가지이다.
1.단 하나의 해 = 역행렬이 존재하는 경우
2.하나의 해도 없는 경우
3.무수히 많은 해를 가지는 경우
이 가능성들을 탐구하기 위한 방법으로 선형 조합을 생각해보자.
A를 벡터들의 집합이 행렬, x를 이 벡터들에 곱해지는 가중치들의 집합인 벡터로 이해한다면 Ax라는 식은 특정한 벡터 공간이 될 것이다.
따라서 b가 이 공간안에 있느냐로 위의 식을 다시 해석할 수 있다.
만약 b가 m차원 실수의 벡터라면 A행렬은 m차원 실수의 n개의 벡터로 이루어진 행렬일 것이다(지금은 벡터공간을 다루고 있다.)
따라서 n>=m라는 부등식이 성립한다. b가 조건없이 A행렬의 벡터 공간에 들어올 수 있으려면 적어도 b의 차원을 모두 표현이 가능한 개수의 벡터가 필요하기 때문이다.
선형 독립이란 어떤 벡터도 다른 벡터로 표현이 가능하지 않는 경우이다.
b의 값들을 모두 포함하는 선형 공간을 만들기 위한 필요조건이자 충분조건은 행렬 A의 벡터들이 선형 독립인 경우이다. 또한 이 행렬이 정방인 행렬이라면 b의 값을 하나로 특정지을 수가 있게 된다. 이런 행렬을 가역행렬이라고 하고, 이렇지 않은 행렬은 특이행렬singular하다고 말한다.
Norms
size of a vector이며 vector X의 Lp norm은 다음과 같다.
이 값은 0,0으로부터 벡터까지의 거리와 같다.
또한 norm을 함수 f라고 생각한다면 아래와 같은 정리를 만족한다.
L2 norm은 Euclidean norm이라고도 불리며 수학적, 컴퓨터적인 연산을 위해서 루트를 생략하고 사용되기도 한다. 또한 벡터의 내적인 XTX로 쉽게 표현이 가능하다. squared L2 norm의 값은 0과 1사이에서 작게 증가하는 모습을 보이기 때문에 머신러닝에서 기피하는 경향이 있다(?)
행렬의 norm은 Frobenius norm으로 구하며 모든 원소들을 제곱해서 더해주면 된다.
Special Kinds of Matrices and Vectors
Diagonal Matrices : 대각 원소의 값들만 0이 아니고, 다른 원소들의 값은 0인 행렬(항등행렬처럼), 대각행렬의 역행렬은 각 원소 1/v를 하면 되고, 정사각행렬일 경우에는 행렬곱을 할경우 연산이 쉬워진다는 장점이 있다.
Symmetric Matrix : A = AT
Unit Vector : ||x|| = 1
Orthogonal : 두 벡터의 내적 xTy = 0이면 두 벡터는 서로 수직이다.
Orthonormal : 벡터들이 orthogonal할 뿐만 아니라 unit vector들이라면 이들은 orthonormal하다.
Orthogonal Matrix : 행의 벡터들과 열의 벡터들이 orthonormal하면 이 행렬은 orthogonal matrix이다. ATA = AAT = I이며, A-1 = AT이다.
Eigendecomposition
행렬의 functional properties를 알 수 있는 방법으로 decomposition을 할 수 있다.
eigenvector는 행렬 A와 곱해져도 오직 크기만 변하는 벡터를 말한다.
Av = lv, scalar l(lambda)은 eigenvector에 대응하는 eigenvalue이다.
위 값은 right eigenvector이며 left eigenvector는 vTA = lvT로 표현이 가능하다.
eigenvector는 일반적으로 unit vector로 만들어서 사용을 한다.
만약 행렬 A가 n개의 linearly independent한 eigenvector를 가진다면 행렬 A는 다음과 같이
decomposition이 가능하다. A = Vdiag(l)V-1로 표현이 가능하다.
아래 그림은 행렬 A로 변환하는 것을 보여준다.
대칭행렬symmetric matrix는 eigendecomposition을 하면 eigenvector가 정규직교행렬orthogonal matrix을 이루는 행렬로 만들어진다. A=QLQT이다. 모든 정방행렬이 고유값 분해가 가능한 것은 아니지만 대칭행렬은 항상 고유값 분해가 가능하며 더구나 직교행렬로 대각화가 가능함을 기억하자.
또한 Ax = lx이므로 고유값이 0이 되면 Ax = 0이 되어서 A행렬의 역행렬이 존재하면 안되게 된다. x벡터는 0이 아닌 벡터이기 때문이다.
또한 nxn 행렬 A가 대칭행렬이고, n개의 고유값 λ1≥λ2≥⋯≥λn과, 이들 각각에 해당하는 단위 고유벡터 u1,⋯,un이 있다고 하자.
이 때, x⊺Ax의 최댓값은 행렬 A의 고유값 중 가장 큰 것(λ1)이고, 이를 최대화하는 x는 λ1에 해당하는 단위 고유벡터 u1이다. 한편, x⊺Ax의 최솟값은 A의 고유값 중 가장 작은 것(λn)이고, 이를 최소화하는 x는 λn에 해당하는 단위 고유벡터 un이다.
또한 eigendecomposition을 이용해서 다음과 det(A), A의 거듭제곱, 역행렬, 대각합, 행렬의 다항식등을 쉽게 알 수 있다.
이미지 출처 : https://darkpgmr.tistory.com/105
Singular Value Decomposition
A = UDVT
A is m x n matrix
U is m x m matrix
D is m x n matrix
V is n x n matrix
U와 V 행렬은 orthgonal matrix이다.
D 행렬은 diagonal matrix인데 그 원소들은 A행렬의 singular values이다.
U 행렬의 열들은 left-singular vectors이다. AAT(symmetric mat)의 eigenvectors이다.
V 행렬의 열들은 right-singular vectors이다. ATA(symmetric mat)의 eighenvectors이다.
The Moore-Penrose Pseudoinverse
모르겠다.
The Trace Operator
Trace of A는 A 행렬의 대각합을 모두 더한 값이다.
Trace값으로 Frobenius norm을 구할 수 있다. ||A|| = Tr(AAT) ** 1/2이다.
이유는 간단한데 AAT의 대각 원소는 각 원소의 제곱의 합으로서 루트를 씌워주면
모든 원소의 제곱의 합의 루트라는 Frobenius norm의 정의와 일치하기 때문이다.
The Determinant
성질에 대해서는 아래 블로그를 참조한다.
https://darkpgmr.tistory.com/103