통계학#1 포아송 분포와 지수 분포

내용은 위키백과에서 가져옴.

푸아송 분포

푸아송 분포(Poisson分布, 영어: Poisson distribution)는 확률론에서 단위 시간 안에 어떤 사건이 몇 번 발생할 것인지를 표현하는 이산 확률 분포이다.

정해진 시간 안에 어떤 사건이 일어날 횟수에 대한 기댓값을 λ라고 했을 때, 그 사건이 k회 일어날 확률은 다음과 같다.

여기서 e는 자연상수이다.

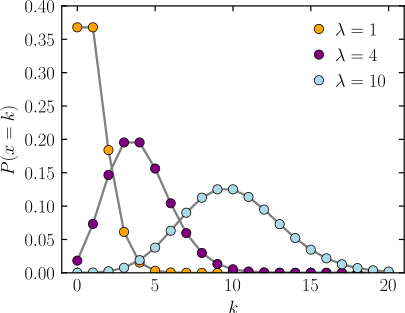
푸아송 분포 확률밀도함수

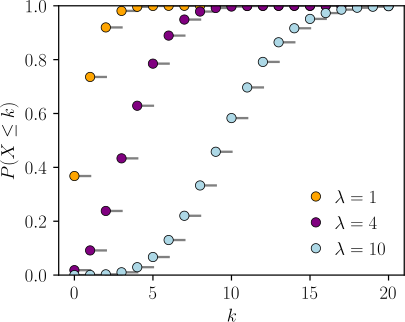
푸아송 분포 누적분포함수

특징

1. 어떤 단위구간(예, 1일)동안 이를 더 짧은 작은 단위의 구간(예: 1시간)로 나눌 수 있고 이러한 더 짧은 단위구간 중에 어떤 사건이 발생할 확률은 전체 척도 중에서 항상 일정해야 한다.
2. 두 개 이상의 사건이 동시에 발생할 확률은 0에 가깝다.
3. 어떤 단위구간의 사건의 발생은 다른 단위구간의 발생으로부터 독립적이다.
4. 특정 구간에서의 사건 발생확률은 그 구간의 크기에 비례한다.
   푸아송분포 확률 변수의 기댓값과 분산은 모두 λ이다.

지수분포

확률론과 통계학에서, 지수분포(指數分布, 영어: exponential distribution)는 연속 확률 분포의 일종이다. 사건이 서로 독립적일 때, 일정 시간동안 발생하는 사건의 횟수가 푸아송 분포를 따른다면, 다음 사건이 일어날 때까지 대기 시간은 지수분포를 따른다. 이는 기하분포와 유사한 측면이 있다.

기댓값과 분산
확률변수 X가 빈도 λ를 모수로 갖는 지수분포를 따른다면, 기댓값은

으로 단위 시간당 사건이 λ회 발생한다면, 사건 사이에 평균적으로 1/λ시간만큼 기다릴 것이라는 것을 의미한다. 분산은 아래와 같다.

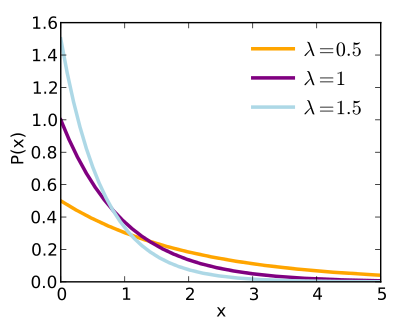
지수분포 확률밀도함수

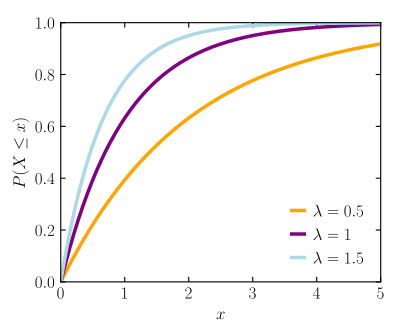
지수분포 누적분포함수