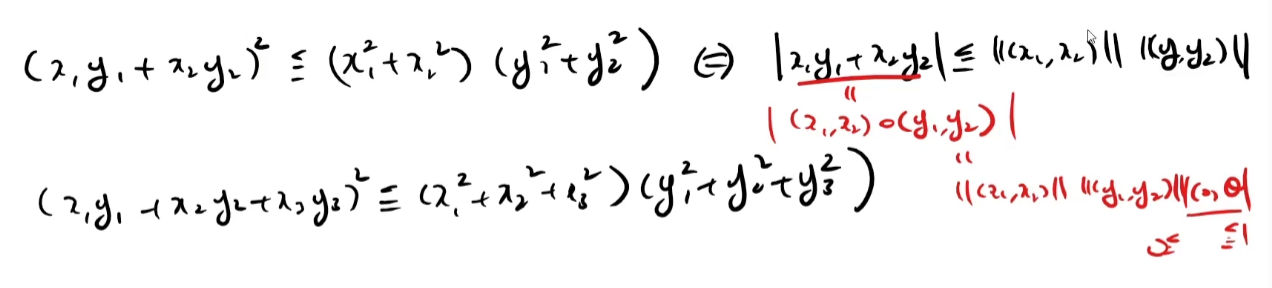
https://youtu.be/kIobK76on3s
한경훈 교수님의 강의 내용을 정리한 문서입니다.
제 요약보다는 교수님의 강의가 훨씬 좋으니 영상을 참고하시면 좋을 것 같습니다.
시소러스
wordnet
수작업으로 만들어진 체계로 머신 러닝과는 정반대의 관계에 있다.
from nltk.corpus import wordnet
wordnet.synsets('car')
# [Synset('car.n.01'),
# Synset('car.n.02'),
# Synset('car.n.03'),
# Synset('car.n.04'),
# Synset('cable_car.n.01')]car = wordnet.synset('car.n.01')
car.definition()
# 'a motor vehicle with four wheels; usually propelled by an internal combustion engine'car.lemma_names()
# ['car', 'auto', 'automobile', 'machine', 'motorcar']# 트리가 2가지 이상의 path로 이루어짐
car.hypernym_paths()
[[Synset('entity.n.01'),
Synset('physical_entity.n.01'),
Synset('object.n.01'),
Synset('whole.n.02'),
Synset('artifact.n.01'),
Synset('instrumentality.n.03'),
Synset('container.n.01'),
Synset('wheeled_vehicle.n.01'),
Synset('self-propelled_vehicle.n.01'),
Synset('motor_vehicle.n.01'),
Synset('car.n.01')],
[Synset('entity.n.01'),
Synset('physical_entity.n.01'),
Synset('object.n.01'),
Synset('whole.n.02'),
Synset('artifact.n.01'),
Synset('instrumentality.n.03'),
Synset('conveyance.n.03'),
Synset('vehicle.n.01'),
Synset('wheeled_vehicle.n.01'),
Synset('self-propelled_vehicle.n.01'),
Synset('motor_vehicle.n.01'),
Synset('car.n.01')]]novel = wordnet.synset('novel.n.01')
car.path_similarity(novel)
# 0.05555555555555555시소러스의 문제점
명확한 것들에 rule로 접근하는 것은 매우 유리하다.
하지만 변화가 심한 것에 rule을 정해서 대응 하는 것은 어렵다.
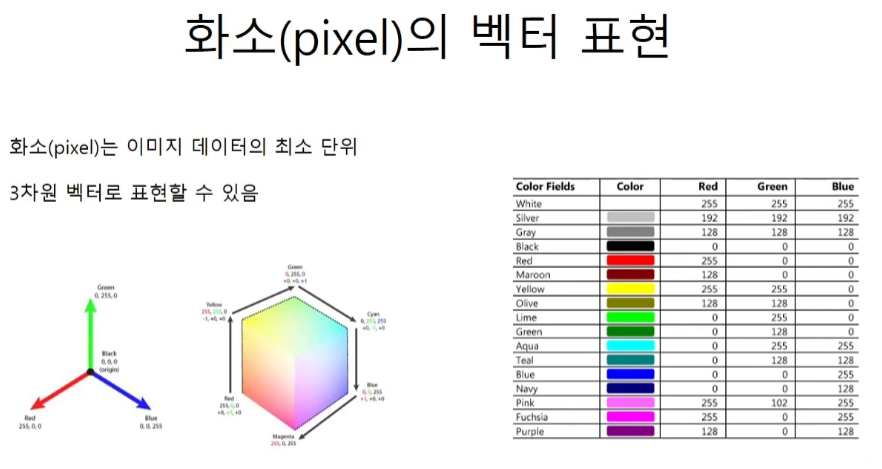
벡터 표현
하나의 픽셀이 3가지 R,G,B 값으로 하나의 색깔을 가지듯 하나의 단어도 특정한 개수의 벡터로 표현이 가능하다.
말뭉치corpus
다만 픽셀은 이미 벡터로 표현이 되어있지만 단어는 전처리를 통해 벡터로 만들어 주어야 한다.
희소sparse 표현
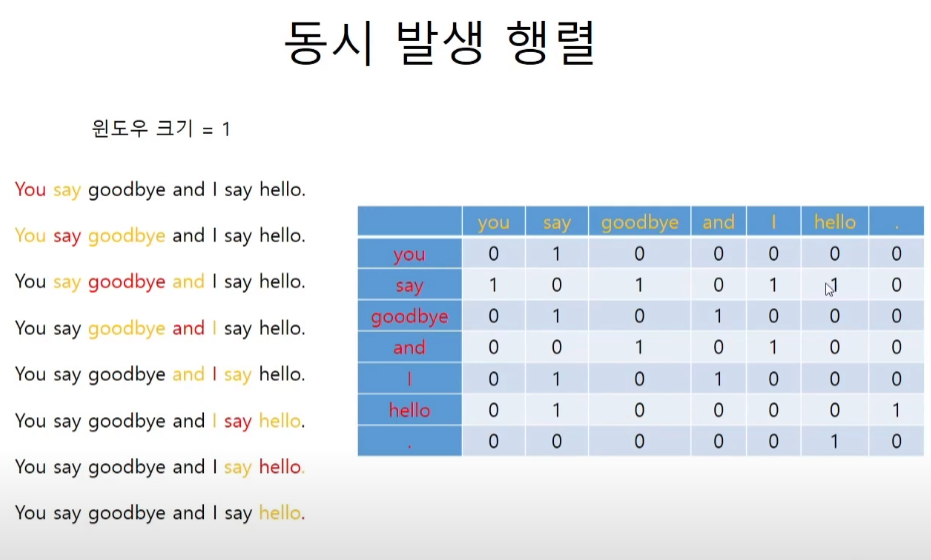
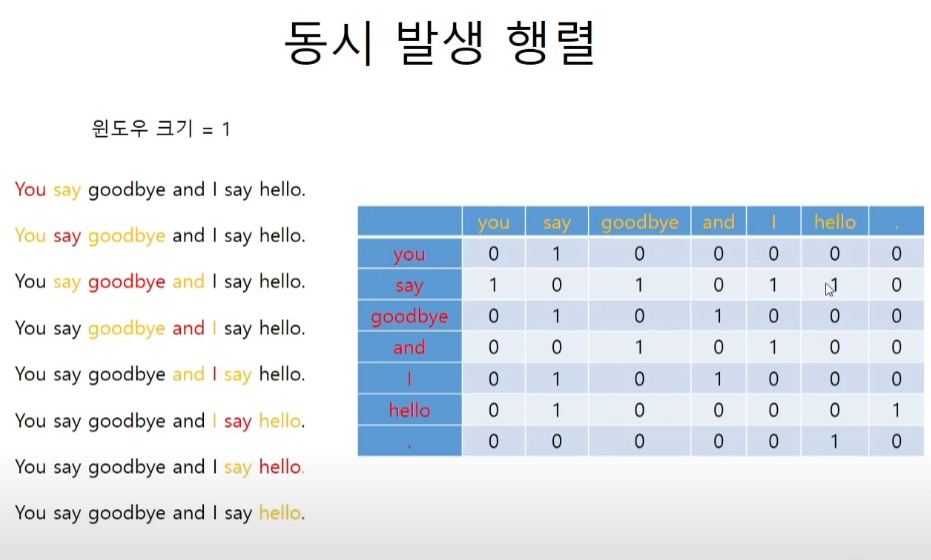
동시 발생 행렬
coaccurance
분포 가설
corpus 코드 구현
def preprocess(text):
text = text.lower()
text = text.replace('.', ' .')
words = text.split(' ')
word_to_id = {}
id_to_word = {}
for word in words:
if word not in word_to_id:
new_id = len(word_to_id)
word_to_id[word] = new_id
id_to_word[new_id] = word
corpus = np.array([word_to_id[w] for w in words])
return corpus, word_to_id, id_to_wordtext = 'you say goodbye and I say hello.'
corpus, wi, iw = preprocess(text)
# corpus = array([0, 1, 2, 3, 4, 1, 5, 6])
# wi = {'you': 0, 'say': 1, 'goodbye': 2, 'and': 3, 'i': 4, 'hello': 5, '.': 6}
# iw = {0: 'you', 1: 'say', 2: 'goodbye', 3: 'and', 4: 'i', 5: 'hello', 6: '.'}동시 발생 행렬 코드 구현
def create_co_matrix(corpus, vocab_size, window_size=1):
'''
동시발생행렬 생성
coupus : 말뭉치, 각 단어는 id로 변환되어 있다.
vocab_size : 사용된 단어의 수
window_size : 윈도우 크기
'''
coupus_size = len(corpus)
co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)
for idx, word_id in enumerate(corpus):
for i in range(1, window_size + 1):
left_idx = idx - i
right_dix = idx + i
if left_idx >= 0:
left_word_id = corpus[left_idx]
co_matrix[word_id, left_word_id] += 1
if right_idx < corpus_size:
right_word_id = corpus[right_idx]
co_matrix[word_id, right_word_id] += 1
return co_matrixmatrix = create_co_matrix(corpus, vocab_size=7, window_size=1)
print(matrix)
[[0 1 0 0 0 0 0]
[1 0 1 0 1 1 0]
[0 1 0 1 0 0 0]
[0 0 1 0 1 0 0]
[0 1 0 1 0 0 0]
[0 1 0 0 0 0 1]
[0 0 0 0 0 1 0]]코사인 유사도
Cauchy-Schwarz 부등식은 벡터의 내적으로 바꿔서 생각하면 좀더 납득이 간다.
루트를 씌우게되면 증명이 시작된다.
코드 구현
코드는 위의 식을 그대로 옮긴 것과 같다.
def cos_similarity(x, y, eps=1e8-8):
'''
x : 벡터
y : 벡터
'''
nx = x / (np.sqrt(np.sum(x ** 2)) + eps)
ny = y / (np.sqrt(np.sum(y ** 2)) + eps)
return np.dot(nx, ny)c0 = word_matrix[wi['you']]
c2 = word_matrix[wi['goodbye']]
cos_similarity(c0, c2, eps=1e-5)
# 0.7070947102747996
# 작은 corpus에서 벡터의 값들이 모여있어서 값들의 변화가 작다.def most_similar(query, word_to_id, id_to_word, word_matrix, top=5):
'''
query : 쿼리, 텍스트
word_to_id : 단어에서 단어 ID로 변환하는 딕셔너리
id_to_word : 단어 ID에서 단어로 변환하는 딕셔너리
word_matrix : 단어 벡터를 정리한 행렬. 각 행에 해당 단어 벡터가 저장되어 있다고 가정한다.
top : 상위 몇 개까지 출력할 지 지정
'''
if query not in word_to_id:
print(f"{query}를 찾을 수 없습니다.")
return
print('\n[query]' + query)
query_id = word_to_id[query]
query_vec = word_matrix[query_id]
# 코사인 유사도 계산
vocab_size = len(id_to_word)
similarity = np.zeros(vocab_size)
for i in range(vocab_size):
similarity[i] = cos_similarity(word_matrix[i], query_vec)
# 코사인 유사도, 내림차순
count = 0
# argsort 큰 순으로 오름차순이다.
for i in (-1 * similarity).argsort():
if id_to_word[i] == query:
continue
print(f"{id_to_word[i]} : {similarity[i]}")
count += 1
if count >= top:
returnmost_similar('you', wi, iw, word_matrix, top=5)
[query]you
goodbye : 0.7071067691154799
i : 0.7071067691154799
hello : 0.7071067691154799
say : 0.0
and : 0.0