개선방법
Mutual Information
크면 클수록 많은 정보를 알려준다.
간단하게 생각하면 보정작업이다.
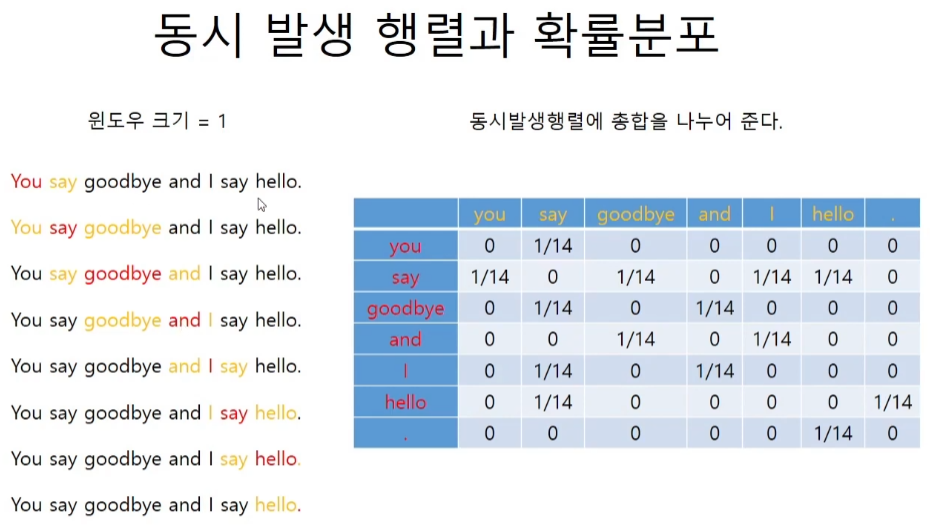
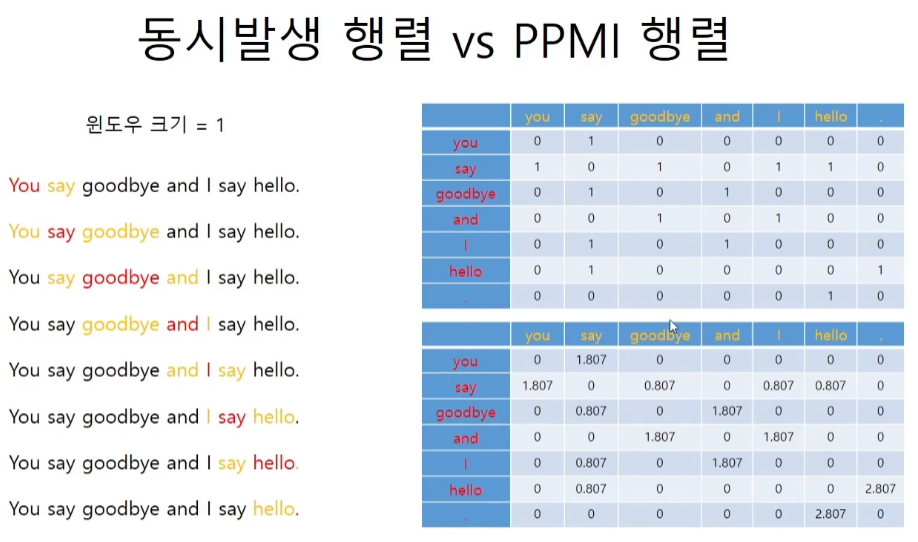
동시 발생 행렬과 PPMI 행렬
1/14는 C(x,y)/N이다.
1 x 14 / 1 x 4 = 3.5 log를 취하면 아래 값이 나온다.
코드구현
def ppmi(C, verbose=False, eps = 1e-8):
'''
C : 동시발생행렬
verbose : 진행상황
'''
M = np.zeros_like(C, dtype=np.float32)
N = np.sum(C)
S = np.sum(C, axis=0)
total = C.shape[0] * C.shape[1]
cnt = 0
for i in range(C.shape[0]):
for j in range(C.shape[1]):
pmi = np.log2(C[i, j] * N / (S[i]*S[j]) + eps)
M[i, j] = max(0, pmi)
if verbose:
cnt += 1
if cnt % (total//100) == 0:
print(f"{100*cnt/total} 완료")
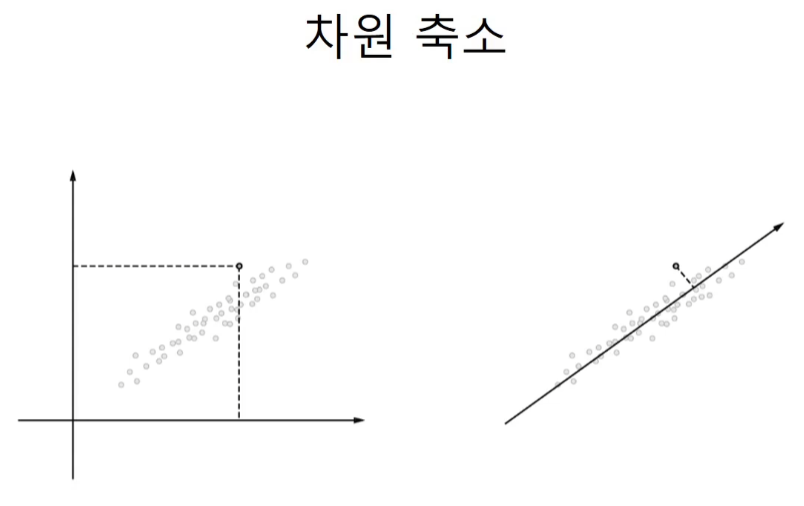
return M차원 축소
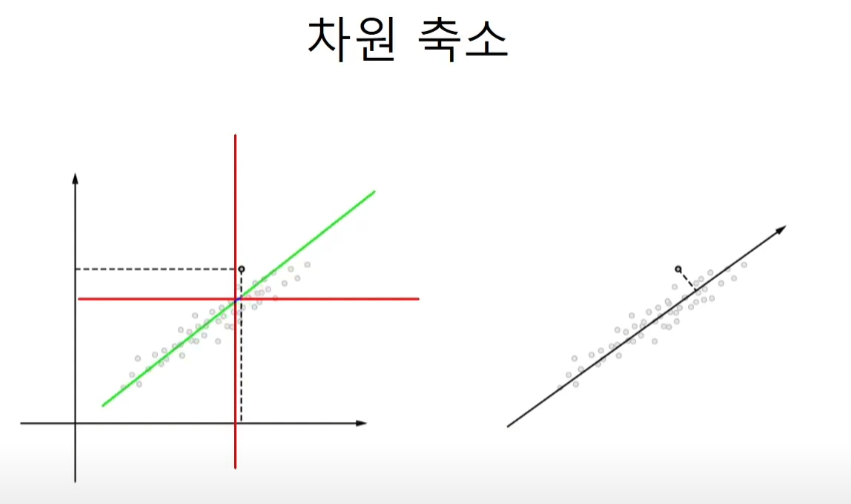
projection 시키는 축을 x축, y축으로 잡는 것이 아니라 데이터와 가까운 직선을 사용하면 정보의 손실을 최소화할 수 있게 된다.
교수님께서 수학적인 증명을 자세하게 해주신다. 깊이 알고 싶다면 영상을 참고하자.
PCA
단어 차원 축소
코드구현
text = "You say goodbye and I say hello."
corpus, wi, iw = preprocess(text)
vocab_size = len(iw)
C = create_co_matrix(corpus, vocab_size, window_size=1)
W = ppmi(C)
U, S, V = np.linalg.svd(W)np.set_printoptions(precision=3)
print(C[0])
print(W[0])
print(U)
# U에서 왼쪽 2개만 살리고 오른쪽 5개를 날린다.
# 이렇게 되면 2차원이되게 된다.
[[-1.110e-16 3.409e-01 -1.205e-01 -3.886e-16 0.000e+00 -9.323e-01
8.768e-17]
[-5.976e-01 0.000e+00 0.000e+00 1.802e-01 -7.812e-01 0.000e+00
0.000e+00]
[-5.551e-17 4.363e-01 -5.088e-01 -2.220e-16 -1.388e-17 2.253e-01
-7.071e-01]
[-4.978e-01 1.110e-16 -2.776e-17 6.804e-01 5.378e-01 0.000e+00
4.177e-17]
[-3.124e-17 4.363e-01 -5.088e-01 -1.600e-16 -1.302e-17 2.253e-01
7.071e-01]
[-3.124e-17 7.092e-01 6.839e-01 -1.600e-16 -1.302e-17 1.710e-01
1.619e-16]
[-6.285e-01 -1.943e-16 4.163e-17 -7.103e-01 3.169e-01 2.220e-16
-5.378e-17]]for word, word_id in wi.items():
plt.annotate(word, (U[word_id, 0], U[word_id, 1]))
plt.scatter(U[:,0], U[:,1], alpha=0.5)
plt.show()
이후에는 ptb 데이터 셋으로 좀더 큰 크기를 대상으로 실험을 해본다.