LSTM
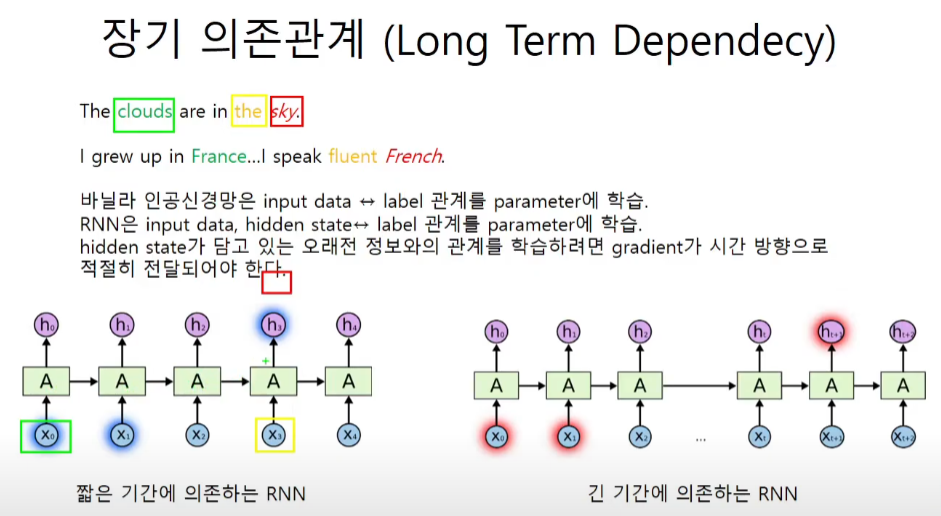
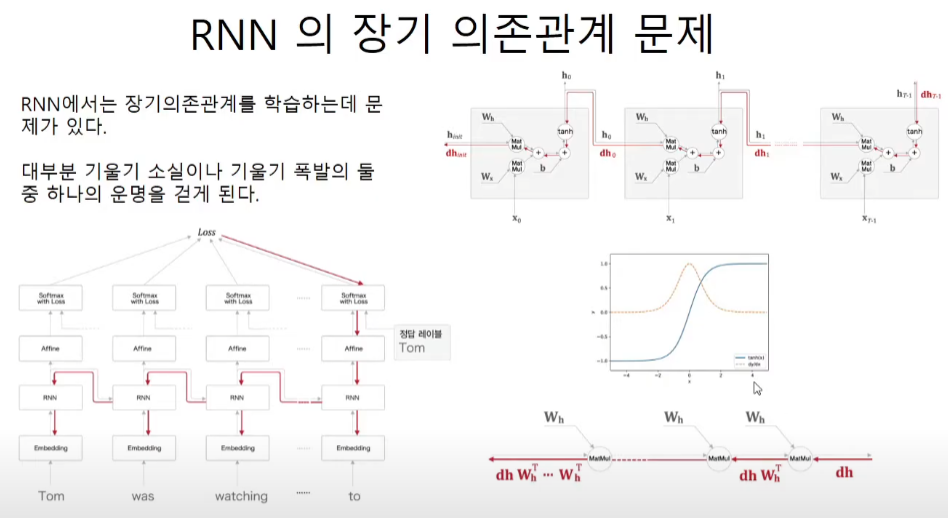
vanila RNN의 문제점
그림에서 잘 보이지 않지만 노란색 박스가 input이고 빨간색 박스가 label이다.
심층신경망을 공부할때 vanishing gradient의 문제를 해결하기 위해서 relu를 사용한다던지, javier/he값으로 가중치를 초기화 한다던지, batch normalization을 도입한다던지 하는 방법을 사용했었다.
tanh함수도 또한 sigmoid와 같이 대부분의 값들이 1보다 작으므로 계속해서 진행이 되면 gradient가 소실이 된다.
특이하게 RNN은 기울기 폭발의 문제를 만들기도 하는데 역전파를 구하기 위해 곱셈을 계속하는 과정에서 이런 현상이 생기게 된다.
따라서 장기의존의 문제를 해결하기 위해서 이대로는 폭발 혹은 소실이므로 다른 해결책이 필요하게 된다.
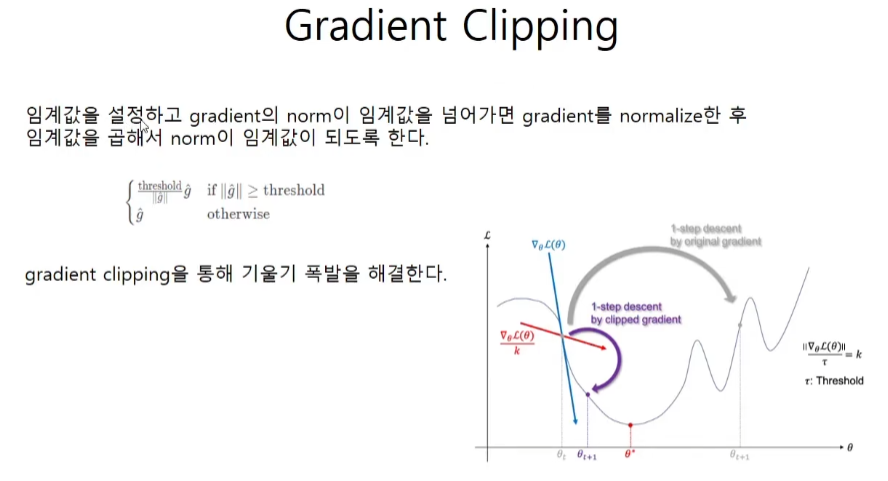
Gradient Clipping
회색의 큰 걸음에서 보라색의 작은 걸음으로 바꿔준다.
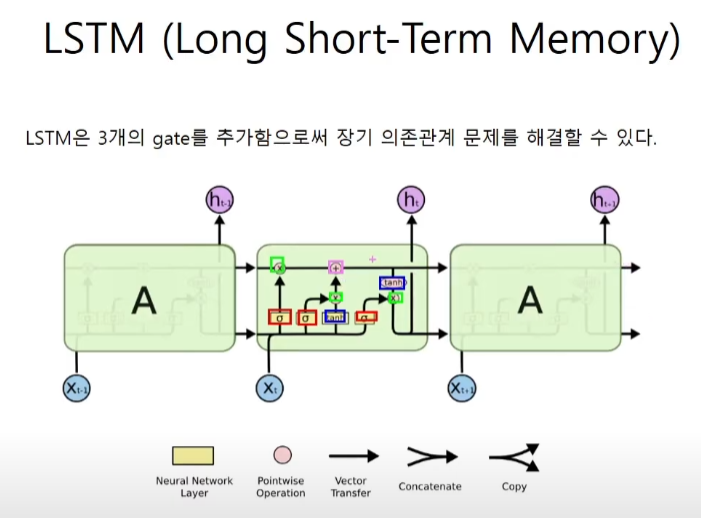
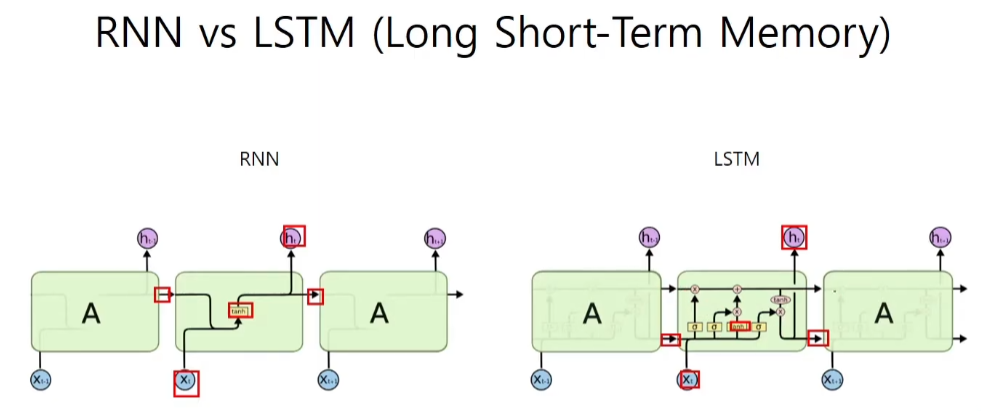
LSTM
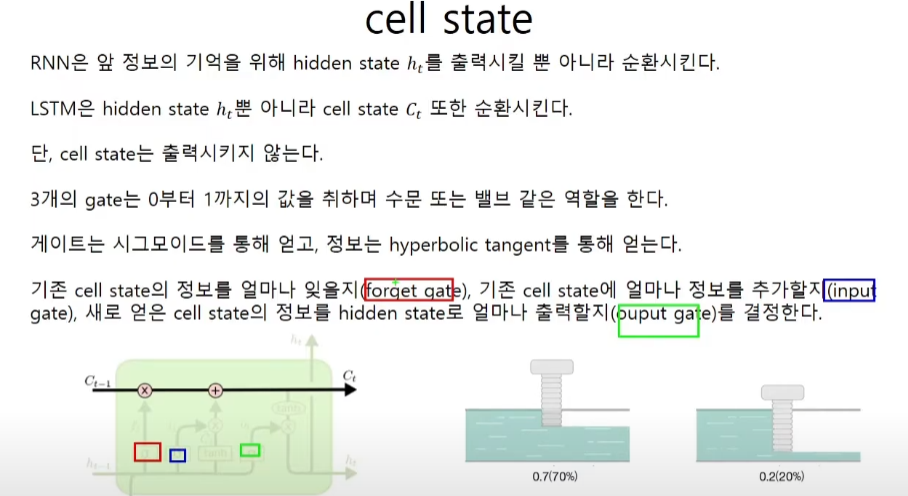
hidden state와 cell state
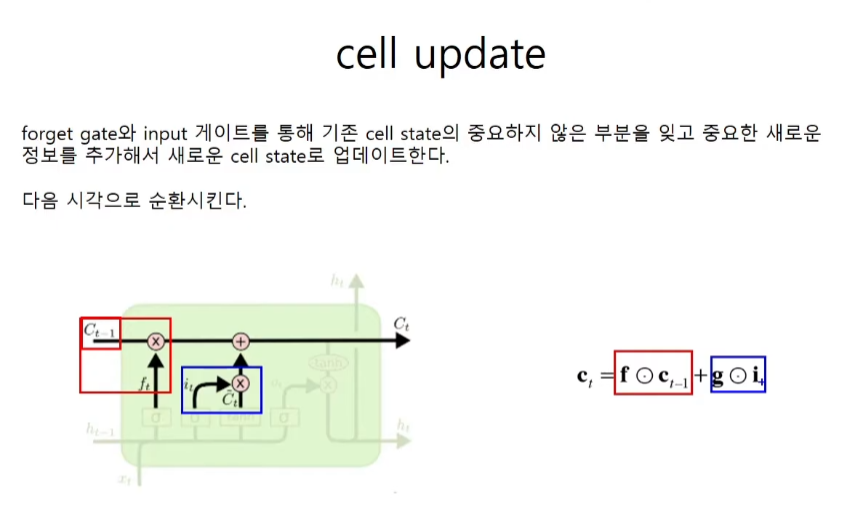
cell state
gate는 affine변환, gate와 대상은 hadamard곱
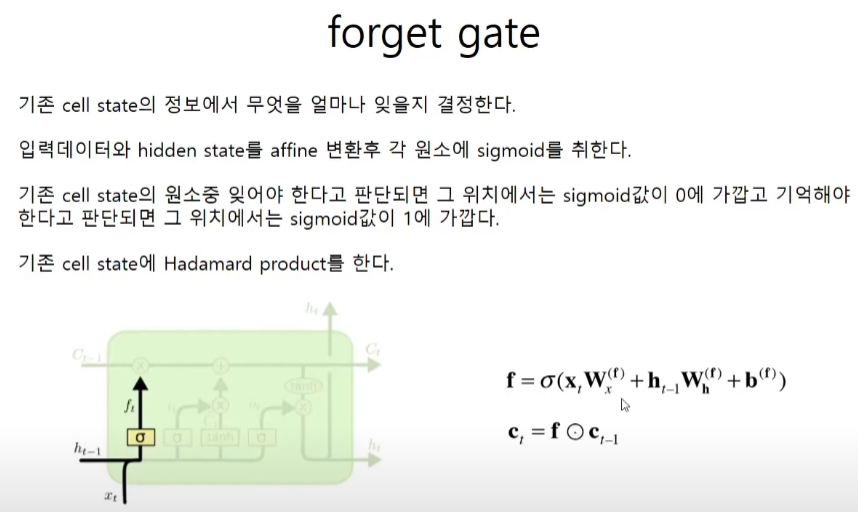
forget gate
이전의 cell state가 ct-1이고 forget gate가 f라면 새로운 cell state는 이 둘의 hadamard product로 계산한다. 가중치는 학습을 통해서 모델이 한다.
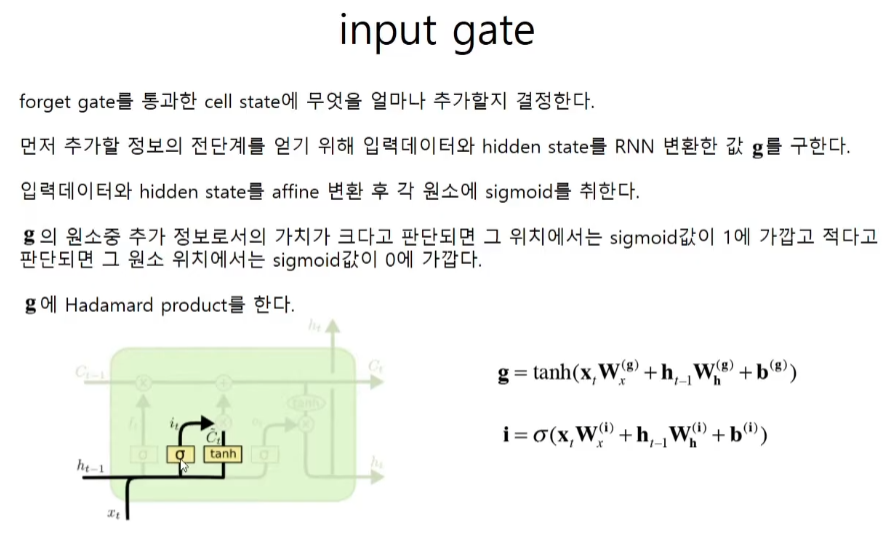
input gate
g는 rnn이고 tanh는 정보값이다. i에서 input gate로서 정보의 중요한 정도를 정한다.
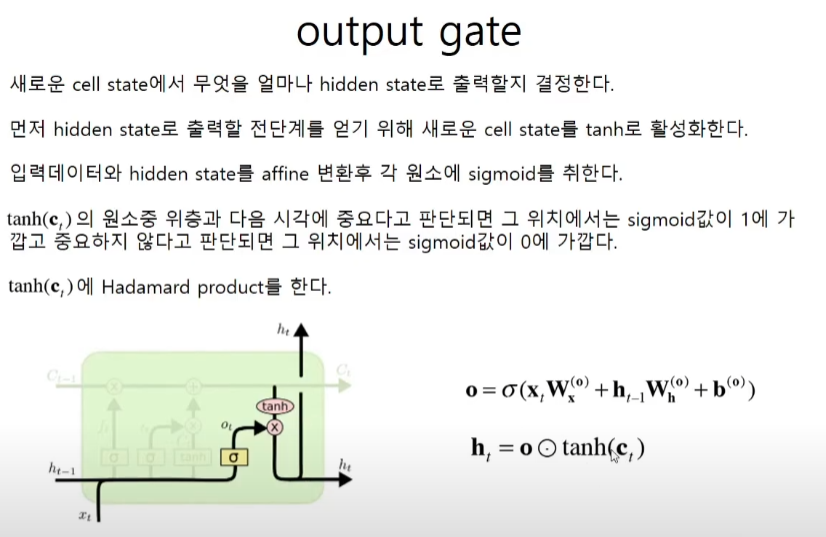
output gate
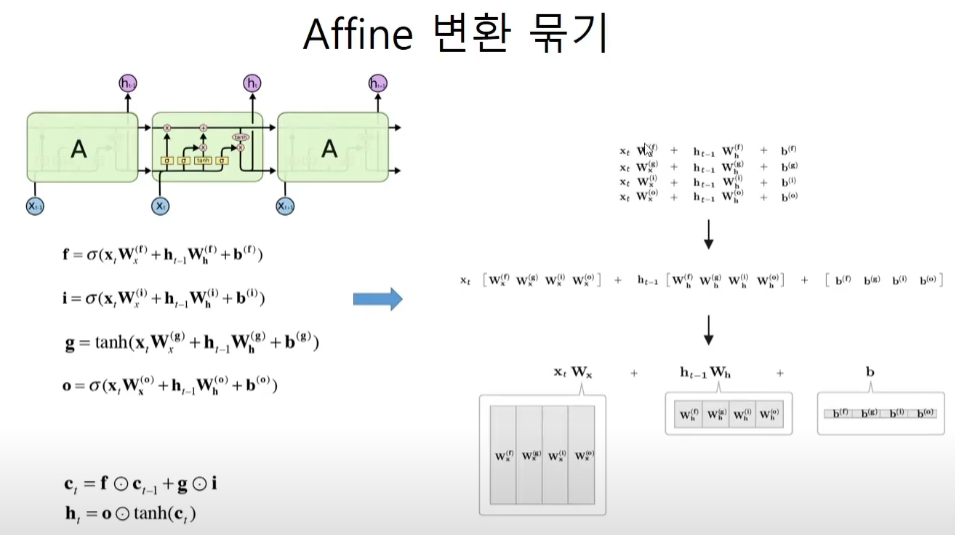
가중치 행렬
밸브는 sigmoid 정보는 tanh이다. f, i, o는 밸브이고, g는 rnn과 동일한 정보이다. 학습할 가중치는 4 + 4 + 4 = 12개이다. 가중치들을 모두 합쳐주면 한번에 계산을 하고 결과값들을 골라쓰면 되므로 계산 속도에 이점이 생긴다.
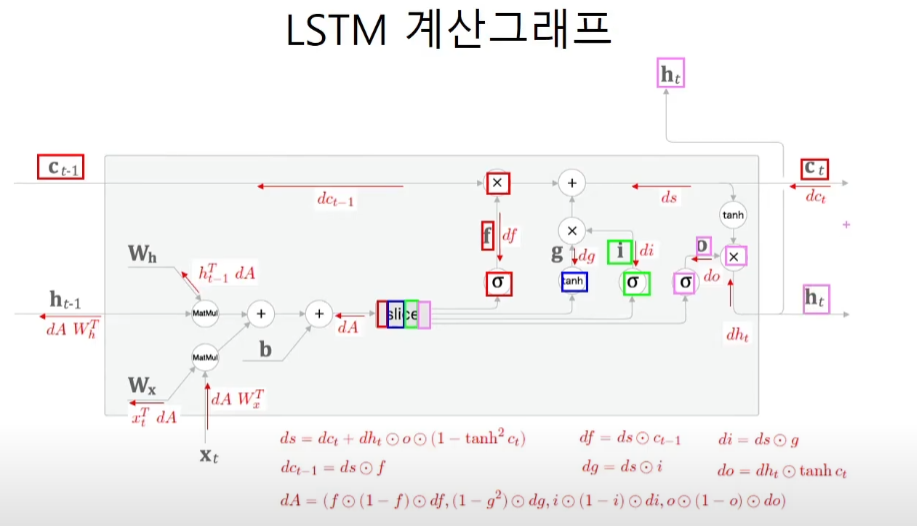
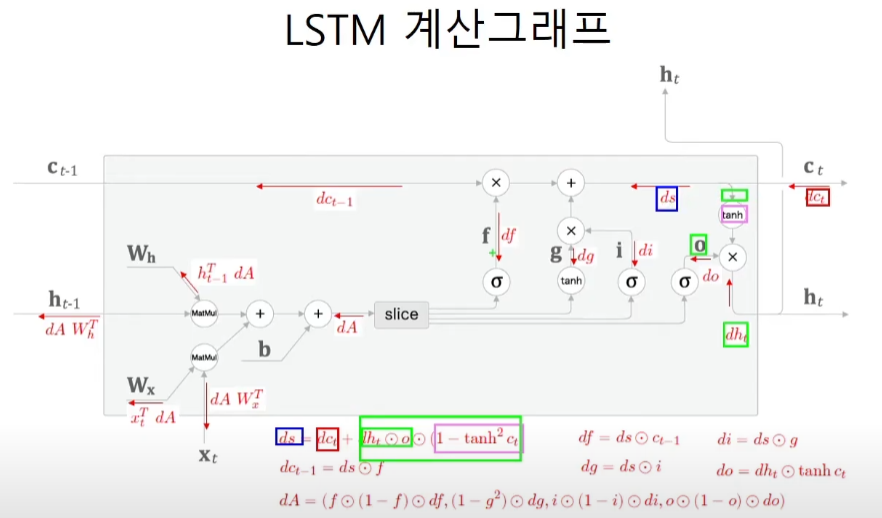
LSTM 계산그래프
밖으로 나가는게 3개이기 때문에 흘러들어오는 미분도 역시 3개이다.
와 역전파가 열라게 복잡하다. 하지만 원리는 역시나 local gradient x upstream gradient라는 것을 이해한다면 된다.
LSTM 코드구현
class LSTM:
def __init__(self, Wx, Wh, b):
'''
parameters
Wx : 입력 x에 대한 가중치 매개변수(4개를 합침)
Wh : 은닉 상태 h에 대한 가중치 매개변수(4개를 합침)
b : 편향(4개를 합침)
'''
self.params = [Wx, Wh, b]
self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
self.cache = none
def forward(self, x, h_prev, c_prev):
Wx, Wh, b = self.params
# 배치 x hidden cell state차원
N, H = h_prev.shape
A = np.dot(x, Wx) + np.dot(h_prev, Wh) + b
f = A[:, :H]
g = A[:, H:2*H]
i = A[:, 2*H:3*H]
o = A[:, 3*H:]
f = sigmoid(f)
g = np.tanh(g)
i = sigmoid(i)
o = sigmoid(o)
c_next = f * c_prev + g * i
h_next = o * np.tanh(c_next)
self.cache = (x, h_prev, c_prev, i, f, g, o, c_next)
return h_next, c_next
def backward(self, dh_next, dc_next):
Wx, Wh, b = self.params
x, h_prev, c_prev, i, f, g, o, c_next = self.cache
tanh_c_next = np.tanh(c_next)
ds = dc_next + (dh_next * o) * (1 - tanh_c_next ** 2)
dc_prev = ds * f
di = ds * g
df = ds * c_prev
do = dh_next * tanh_c_next
dg = ds * i
di *= i * (1 - i)
df *= f * (1 - f)
do *= o * (1 - o)
dg *= (1 - g ** 2)
# horizontal 수평으로 쌓기
dA = np.hstack((df, dg, di, do))
dWh = np.dot(h_prev.T, dA)
dWx = np.dot(x.T, dA)
db = dA.sum(axis=0)
self.grads[0][...] = dWx
self.grads[1][...] = dWh
self.grads[2][...] = db
dx = np.dot(dA, Wx.T)
dh_prev = np.dot(dA, Wh.T)
return dx, dh_prev, dc_prevTimeLSTM 코드구현
class TimeLSTM:
def __init__(self, Wx, Wh, b, stateful=False):
self.params = [Wx, Wh, b]
self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
self.layers = None
self.h, self.c = None, None
self.dh = None
self.stateful = stateful
def forward(self, xs):
Wx, Wh, b = self.params
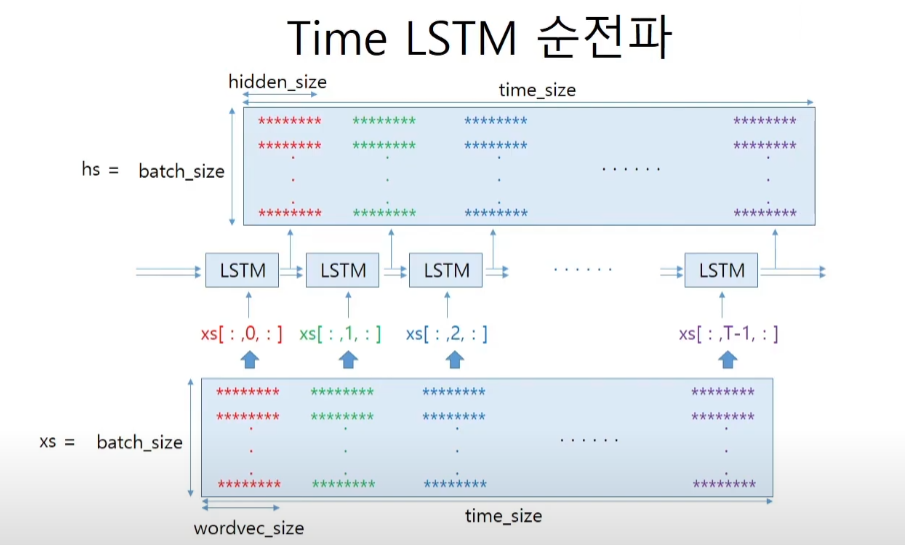
# T는 timeblock의 size이다. 앞선 예시에선 10개였다.
# N은 배치의 개수, D는 embedding vector의 크기이다.
N, T, D = xs.shape
H = Wh.shape[0]
self.layers = []
hs = np.empty((N, T, H), dtype='f')
if not self.stateful or self.h is None:
self.h = np.zeros((N, H), dtype='f')
if not self.stateful or self.c is None:
self.c = np.zeros((N, H), dtype='f')
for t in range(T):
layer = LSTM(*self.params)
self.h, self.c = layer.forward(xs[:, t, :], self.h, self.c)
hs[:, t, :] = self.h
# LSTM들을 묶어놓는 리스트
self.layers.append(layer)
return hs
def backward(self, dhs):
Wx, Wh, b = self.params
N, T, H = dhs.shape
D = Wx.shape[0]
dxs = np.empty((N, T, D), dtype='f')
dh, dc = 0, 0
grads = [0, 0, 0]
for t in reversed(range(T)):
layer = self.layers[t]
dx, dh, dc = layer.backward(dhs[:, t, :] + dh, dc)
dxs[:, t, :] = dx
for i, grad in enumerate(layer.grads):
grads[i] += grad
for i, grad in enumerate(grads):
self.grads[i][...] = grad
self.dh = dh
return dxs
def set_state(self, h):
self.h, self.c = h, c
def reset_state(self):
self.h, self.c = None, None