[밑바닥부터 시작하는 딥러닝2] #9 RNNLM의 학습과 평가

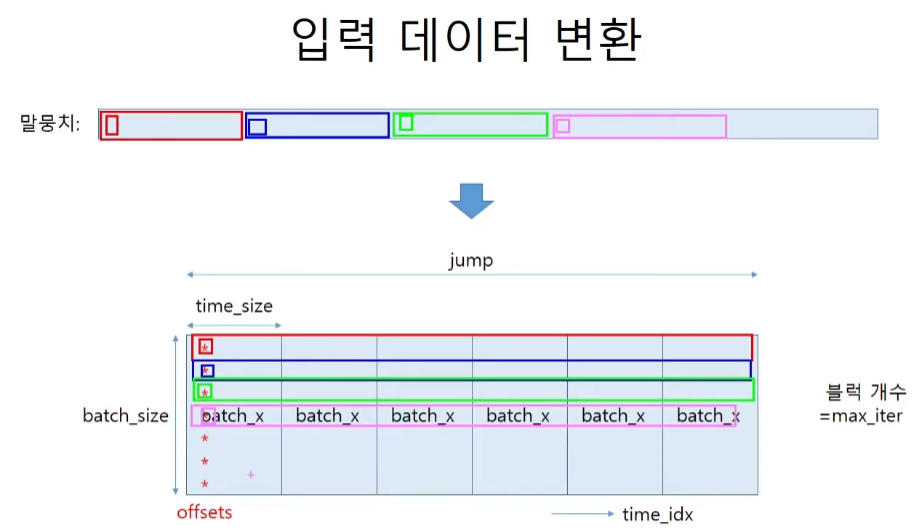
RNNLM의 구조 복습

jump는 가로의 길이 offset은 jump의 첫번째, 두번째, 세번째... 가장 앞 단어를 가리킨다.
시계열 데이터는 데이터를 랜덤하게 샘플링할 수 없다. 그래서 mini-batch를 하는 방식이 조금 특이해진다.

순서대로 자른다는 원리를 PTB에 적용한다.

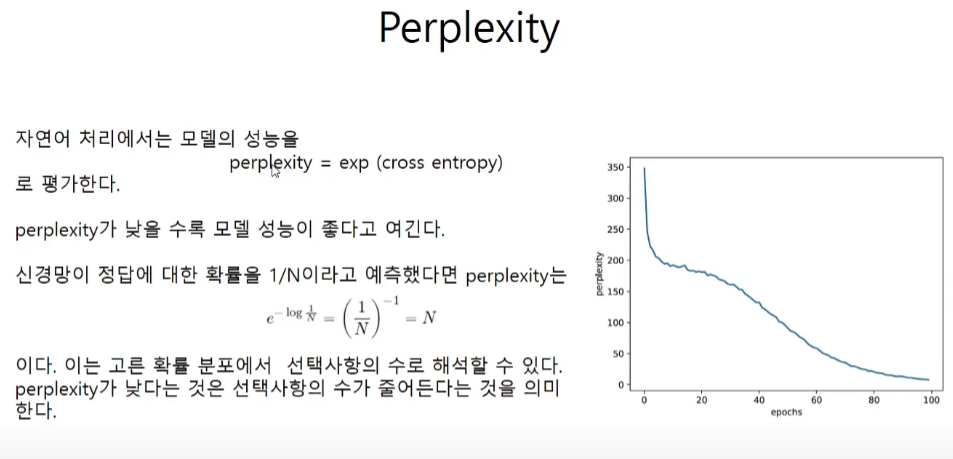
perplexity

cross entropy에다가 exp를 취한 값이다.

학습 코드구현

import matplotlib.pyplot as plt
import numpy as np
from optimizer import SGD
import ptb
from simple_rnnlm import SimpleRnnlm

batch_size = 10
wordvec_size = 100
hidden_size = 100
time_size = 5
lr = 0.1
max_epoch = 100

corpus, word_to_id, id_to_word = ptb.load_data('train')
corpus_size = 1000
corpus = corpus[:corpus_size]
vocab_size = int(max(corpus) + 1)

# you 부터 hello까지
xs = corpus[:-1] 
# say 부터 .까지
ts = corpus[1:]
data_size = len(xs) # 999
print(f"말뭉치 크기 : {corpus_size}, 어휘 수 : {vocab_size}")

# batch 블록의 개수와 같다.
# 블록의 사이즈는 가로 * 세로이다.
max_iters = data_size // (batch_size * time_size)
time_idx = 0
total_loss = 0
loss_count = 0
ppl_list = []

model = SimpleRnnlm(vocab_size, wordvec_size, hidden_size)
optimizer = SGD(lr)

jump = (corpus_size - 1) // batch_size # 99
offsets = [i * jump for i in range(batch_size)] # 0, 99, 198, ..., 891

for epoch in range(max_epoch):
    # 매 iter마다 batch 블록을 하나씩 해나간다.
    for iter in range(max_iters):
        batch_x = np.empty((batch_size, time_size), dtype='i')
        batch_t = np.empty((batch_size, time_size), dtype='i')
        for t in range(time_size):
            for i, offset in enumerate(offsets):
                batch_x[i, t] = xs[(offset + time_idx) % data_size]
                batch_t[i, t] = ts[(offset + time_idx) % data_size]
            time_idx += 1
            
        # 기울기를 구하여 매개변수 갱신
        loss = model.forward(batch_x, batch_t)
        model.backward()
        optimizer.update(model.params, model.grads)
        total_loss += loss
        loss_count += 1
    
    # 에폭마다 perplexity 계산
    ppl = np.exp(total_loss / loss_count)
    print(f"|에폭 {epoch+1}| perplexity {ppl:.2f} ")
    ppl_list.append(float(ppl))
    total_loss, loss_count = 0, 0
    
# 그래프 그리기
x = np.arange(len(ppl_list))
plt.plot(x, ppl_list, label='train')
plt.xlabel('epochs')
plt.ylabel('perplexity')
plt.show()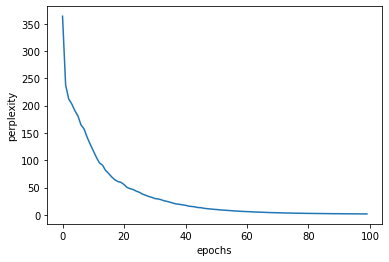

평가

강의 내용은 여기에서 끊긴채로 성능이 안좋다고라고만 하셔서 perplexity 숫자가 얼마나 나쁜건지 감이 안오기도 해서 직접 성능을 평가해보기로 했다. 우선 모델에 inference 메소드를 만들어서 평가값을 보고 그 다음에 정답인 batch_t와 비교해보았다.

infer = model.inference(batch_x)
infer.shape # (10, 5, 418)

infer_most = infer.argmax(axis=2)
infer_most

####################################
array([[108,  98, 166,  26,  64],
       [ 93,  79,  42,  26, 133],
       [ 24, 338,  42, 164,  72],
       [ 24,  32,  68, 181,  24],
       [390,  24, 338,  27, 218],
       [  6,   7,  35,  64,  81],
       [ 76, 160,  64, 220,  73],
       [ 24,  26,  24,  32,  26],
       [229, 339, 108,  26,  24],
       [ 98,  24,  35,  26, 212]], dtype=int64)

batch_t

####################################
array([[243, 108, 244, 172,  48],
       [278, 276,  42,  26,  61],
       [142, 306,  93, 307,  42],
       [181,  32, 351, 352, 353],
       [307,  64, 220,  35, 389],
       [  1,   2,   3,   4,   5],
       [ 76,  77,  64,  78,  79],
       [ 26,  98,  56,  40, 128],
       [ 32,  26, 175,  98,  61],
       [209,  80, 197,  32,  82]], dtype=int32)

두번째로 높은 확률로 예측한 값들을 보아도 성능이 확실히 안좋다는 것을 알 수 있다.

infer.argsort()[:,:,-2]

####################################
array([[308, 373,  42, 154,  24],
       [ 27,  26,  48,  64, 160],
       [ 42,  93, 154,  98, 160],
       [373,  35,  26,  87, 113],
       [113,  42,  61, 101,  26],
       [ 11,  24, 138,  61,  34],
       [187, 148, 159,  61, 342],
       [ 54,  32,  24,  42, 148],
       [229, 212, 160,  24,  24],
       [160, 153,  42,  26, 254]], dtype=int64)