embedding 층
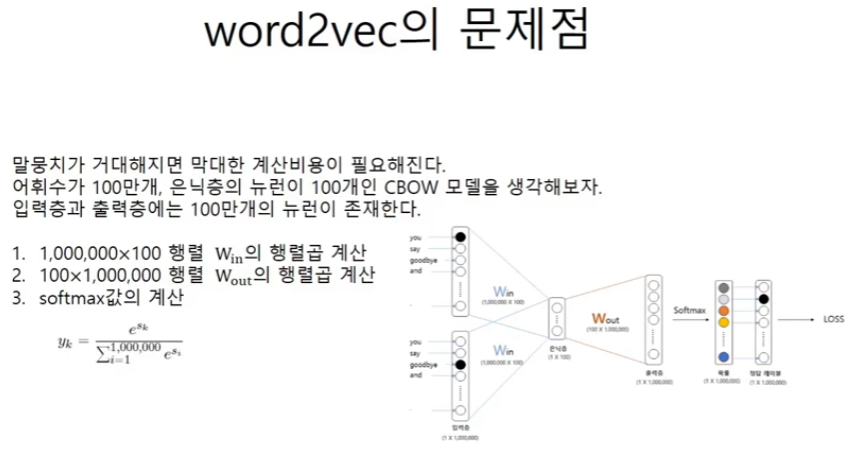
word2vec의 문제점
상용화된 모델에서 사용하기에 지금의 모델 구조는 계산비용이 지나치게 커지게 된다.
가령 PTB데이터 셋은 1만개의 corpus를 가지는데 구글 뉴스의 경우에는 300만개의 corpus를 가진다.
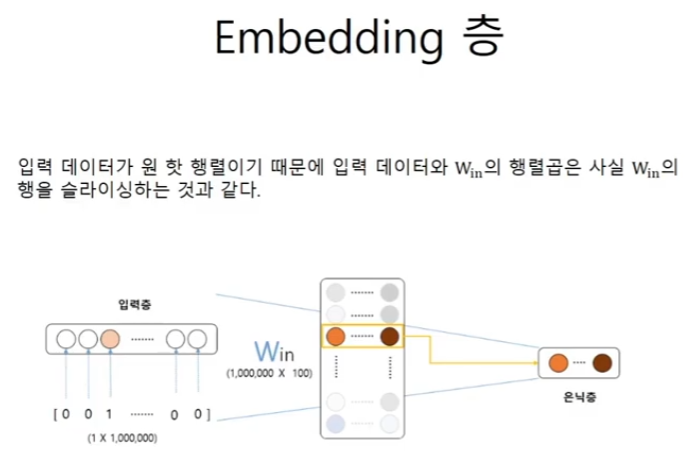
embedding 층
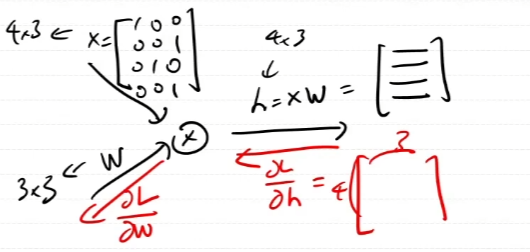
왼쪽 부분의 연산은 one-hot vector를 이용한다.
one-hot vector는 슬라이싱과 같다.
하나의 인풋에 대해서 생각해보자.
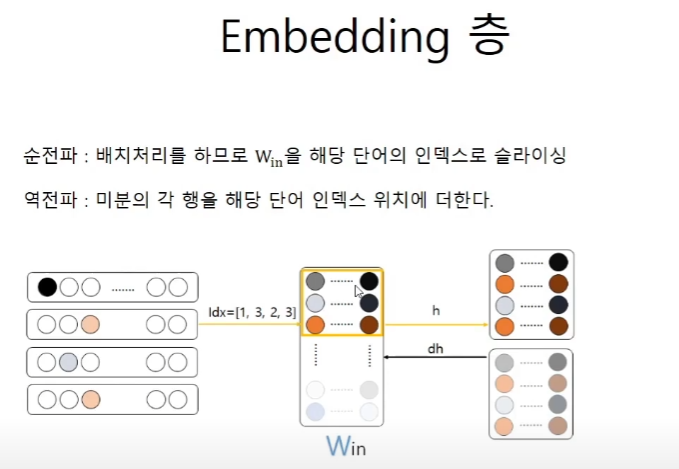
여러개의 인풋에 대해서 생각해보자.
코드 구현
embedding이라고 해서 헷갈릴 수 있지만, 이 층에서 하는 일은 win or wout에 대해서 idx에 맞춰서 그 가중치들을 슬라이싱 해주는 것이다. 즉, 계산 비용을 줄이기 위해서 실질적으로 계산이 되는 가중치의 값들만을 뽑아주는 역할이다.
class Embedding:
def __init__(self, W):
self.params = [W]
self.grads = [np.zeros_like(W)]
self.idx = None
def forward(self, idx):
W, = self.params
self.idx = idx
out = W[idx]
return out
def backward(self, dout):
dW, = self.grads
dW[...] = 0
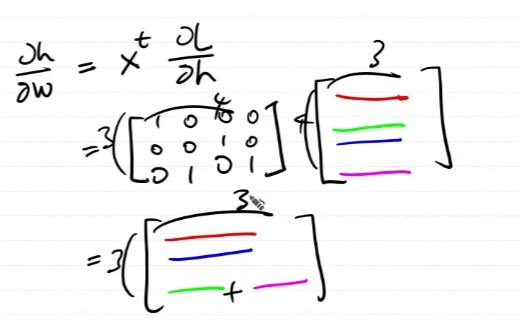
# dW에대가 idx의 순서에 맞춰서 dout의 각 행을 더해준다.
np.add.at(dW, self.idx, dout)
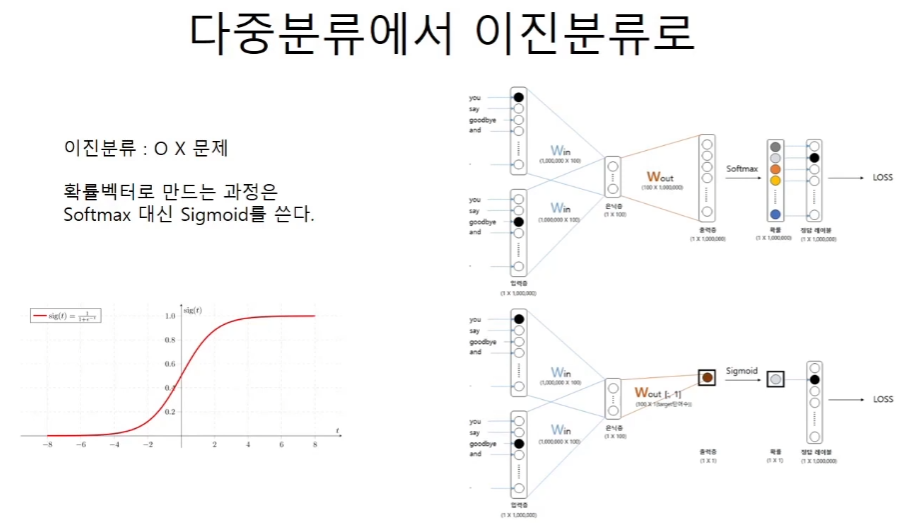
return None다중분류에서 이진분류로
백만개의 가능성을 모두 검토하는 것이 아니고, 1개의 후보를 선정해서 그 후보일 확률을 구한다.
sigmoid는 활성화 함수와 이진 분류에서의 확률로 바꾸어주는 2가지의 역할을 할 수 있다.
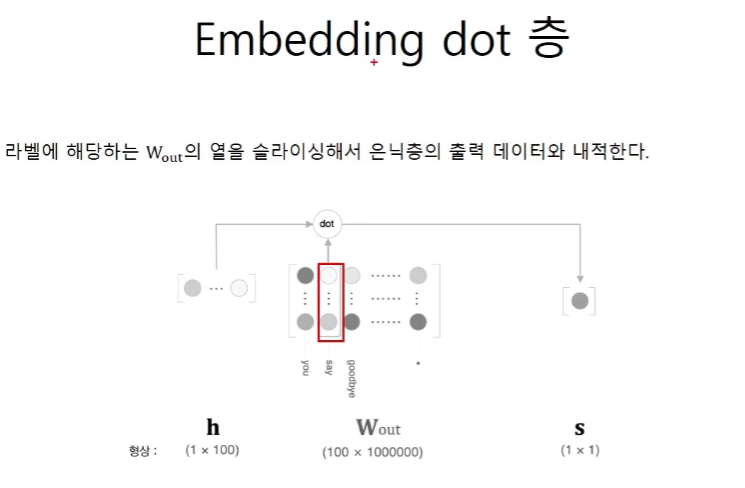
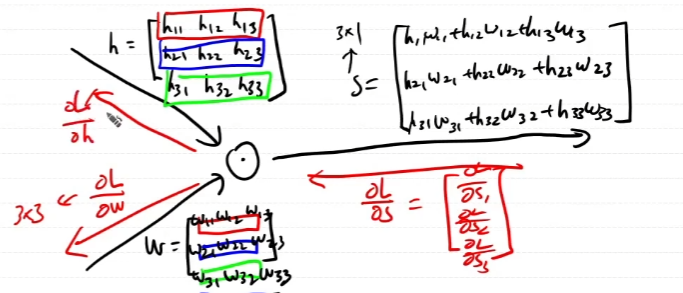
h 행렬 각각 행의 context의 중심인 target의 index를 바탕으로 100x1000000개의 행렬을 추려낸다. 그 추려낸 행렬이 w다. 이 둘의 연산은 행렬곱이 아니고 내적이다.
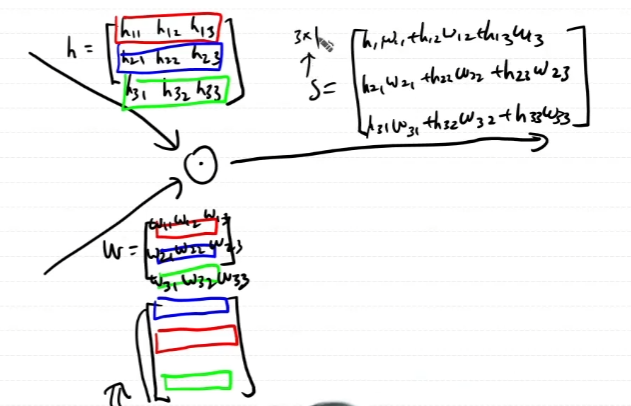
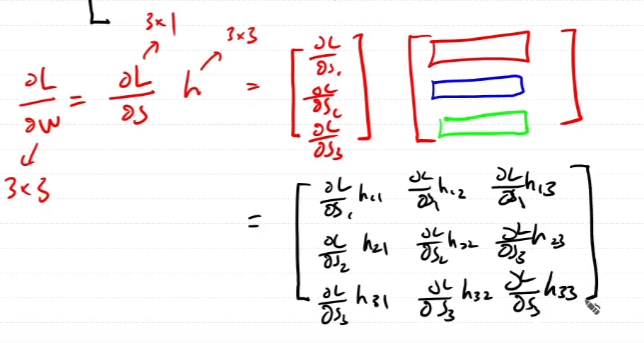
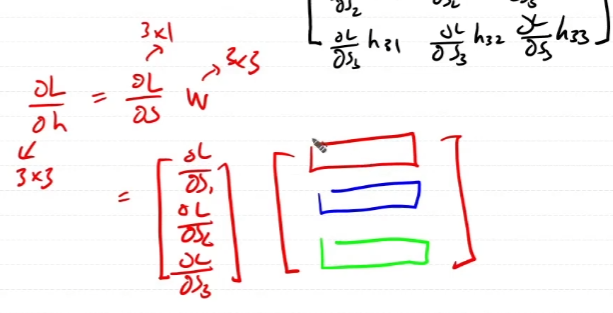
행렬곱이 아닌 element-wise dot product의 역전파를 구해보자.
곱하기니까 역전파도 dout과의 곱으로 계산이 되어야할텐데 행렬곱이 아닌 묘한 형태의 곱이된다.
역전파를 통해 곱셈을 하는 방식에 대한 구체적인 증명은 없다. 하지만 형태적으로 보았을때, scalar를 곱해주는 것으로 이해를 하고 넘어가기로 한다.
코드구현
class EmbeddingDot:
def __init__(self, W):
self.embed = Embedding(W)
self.params = self.embed.params
self.grads = self.embed.grads
self.cache = None
def forward(self, h, idx):
# target_W는 wout에서 뽑아온 행렬이다.
target_W = self.embed.forward(idx)
# s 값을 구한다.
out = np.sum(target_W * h, axis=1)
self.cache = (h, target_W)
return out
def backward(self, dout):
h, target_W = sefl.cache
dout = dout.reshape(dout.shape[0], 1)
# broadcasting을 이용해서 dout만큼의 scalar곱을 해주게 된다.
dtarget_W = dout * h
# embed에서 wout을 idx에 맞게 빼오는 작업을 했으니 정확한
# dout을 구하기 위해서는 다시 돌려주는 작업을 해야한다.
self.embed.backward(dtarget_W)
dh = dout * target_W
return dh