Disjoint Set(서로소 집합)은 서로 배타적인 원소를 가진 두 집합. 공통되는 원소를 가지지않은 두 집합을 말한다.
여기서 해당 알고리즘은 Disjoint Set 자료구조를 사용하여, 서로 다른 두 원소가 같은 집합에 속해있는지를 판별하는데 유용하게 사용된다.
이때 서로 배타적인 원소를 다루므로, 합연산시에, 겹치는 원소를 고려하지않고 직관적인 접근이 가능하다.
이때 Disjoint Set의 집합은 트리 구조로 구현하는데, 이래야 앞서말한 두 원소가 같은 집합인지 판별(두 집단의 루트노드가 같은지 판별)이 쉽다.
따라서, 트리를 구성할때는 자식노드가 자신의 부모노드가 무엇인지만 알도록 짜면된다. (1차원배열활용시 인덱스=원소, 값=부모노드번호)
0. Find
임의의 원소하나가 자신의 부모노드를 타고 올라가며 루트노드가 무엇인지 알아내는 과정
1. Path Compression(경로 압축)
Find 과정에서 방문한 모든 원소를 매번 루트원소를 부모원소로 갱신 하는 과정이다.
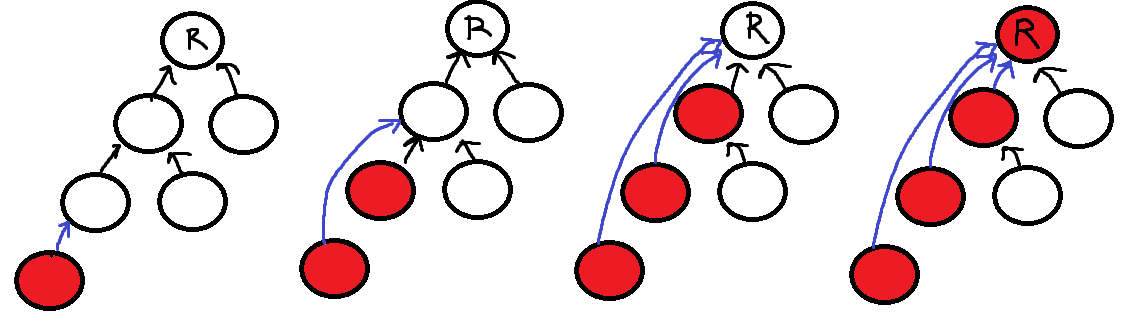
맨 왼쪽부터 맨 아래 빨간원소가 Find연산을 하는 원소라 생각하면 이 원소부터 부모원소를 찾아가며 매번 자신의 부모노드를 루트노드인것으로 갱신해주면된다. 결론적으로 루트노드를 만나는순간
방금까지 탐색한 모든 원소가 이 루트노드를 가리키게 된다.
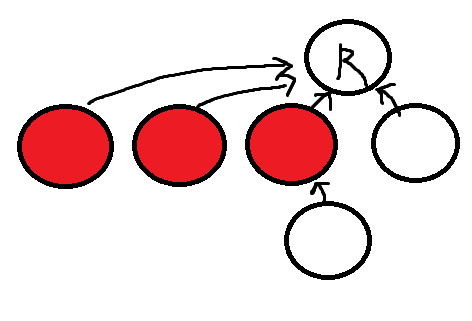 즉 경로압축은 Find할때마다 트리구조를 일부 평평하게 만들어 결과적으로 모두 루트원소를 가리키게 하는 과정이다.
즉 경로압축은 Find할때마다 트리구조를 일부 평평하게 만들어 결과적으로 모두 루트원소를 가리키게 하는 과정이다.
이후 그림의 빨간원소들은 Find연산을 할때 모두 O(1) 시간복잡도만에 루트원소를 찾을 수 있고 이는 앞서말한 두 원소가 같은 집합에 속하는지 쉽게 판별해 준다.
2. Union
알고리즘 사용단계에서 서로 다르던 두 집합에대한 합연산을 사용해야 할 때가 있다. 이때는 하나의 집합을 다른 집합에 포함 시키는것으로 구현한다.
- 즉, 원소 하나하나 부모노드를 수정하는것은 비효율적
- A집합의 루트노드를 B집합의 임의의 자식 노드의 자식으로 합친다면, 이후 A집합의 임의의 원소가 자신의 루트노드(사실상 B집합의 루트노드)를 찾는과정( Find )에서 비효율적이게 된다.
- 따라서 A집합의 루트노드를 B집합의 임의의 자식노드가 아닌 루트노드의 자식노드로 수정하면된다.
이때 N개의 원소가 서로 다른 집합(처음단계로 N개의 집합이라고 생각해보자. 아직 Disjoint Set구조가 되기전)에 속해있을때, 임의의 두 집합을 합쳐가는 과정에서
최악의 경우 N ~ N-1 ~ N-2 ~ 2 ~ 1 번으로 한줄로 된 선형 트리 구조가 생길 수 있다.
이런 최악의 경우에 맨끝인 1번원소가 자신의 루트원소를 찾을때 2번부터 N번까지의 부모원소를 모두 확인하면서 찾기때문에 최악의 경우 O(트리의 크기)만큼의 시간복잡도가 소요된다.
따라서, Union 과정에서, 이런 경우를 막기위해 아래의 두가지 방법이 존재한다.
3. Rank Compression(랭크 압축)
Union과정에서 한 집합을 다른 집합의 루트노드의 자식노드로 삽입하는것을 원칙으로 한다.
3-1. 트리의 깊이가 작은 집합을 큰 집합에 합한다.
이때 트리구조는 경로압축 과정등을 거치지 않았다면 부모노드의 자식노드가 무조건 2개인 이진트리 구조를 띄고있을 것이다. 따라서 합친 트리의 깊이는 최대 1 증가한다. 또, 트리의 크기는 더 작은 트리의 크기가 N이면 최소 2N이상 증가하게된다.
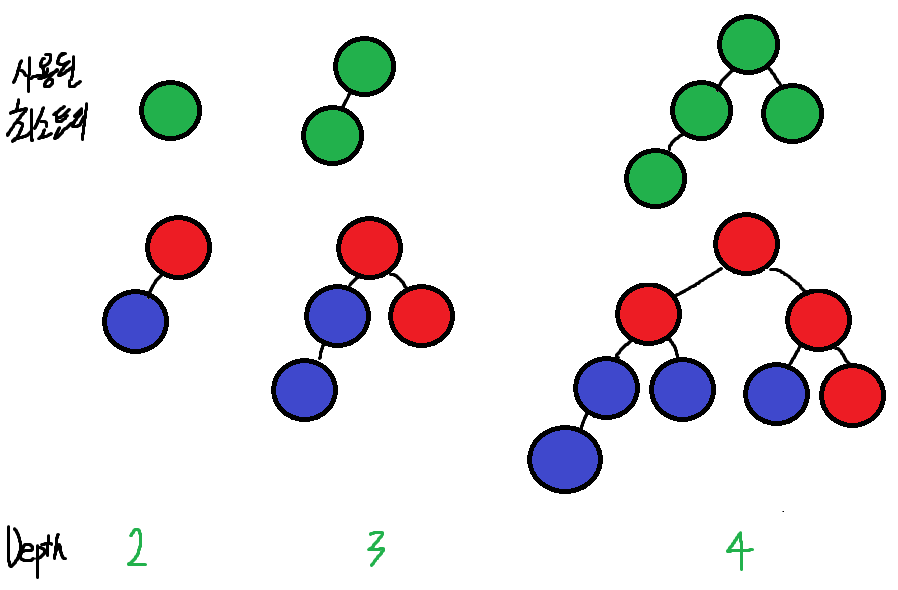
그림처럼, 두 이진트리가 합쳐진후 깊이가 2, 3, 4, ''' 가 되는 경우를 생각해보자. 최소한의 트리는 초록색으로 표시된 트리들이다.
합쳐지고 난뒤 트리의 총 크기는 작은 트리의 2배로 커진것을 볼 수 있다. (전체트리 총 크기 2, 4, 8)
이 경우는 최소한의 트리므로 따라서 합쳐진후 전체 집합의 총 크기는 작은 집합의 크기의 2배이상으로 늘어나게 된다.
또, 깊이는 최대 1 깊어진다.
3-2. 트리의 크기가 큰 집합을 작은 집합에 합한다.
이경우는 역발상인데 4-1과 같은 논리로 최악의 경우 트리의 높이가 O(log N)이 됨을 이용한다.
주로 사용하지 않는 방식이므로 넘어가겠다.
4. 실제 사용시
이제 배운 Path Compression 과 Rank Compression을 모두 사용한다면 Disjoint Set Union의 시간복잡도는 O( a(N) ) (a(N)은 상수에 가깝다.)로 작동한다. 보통 경로압축만으로도 문제를 빠르게 풀수있으나, 문제 특성상 트리구조를 변경하면 안되는경우, 랭크압축을 이용하여 최소한
O(log N)의 시간복잡도를 얻어낼 수 있다.
즉, 1차원크기를 가지는 자료구조를 선언하여 자식노드가 부모노드를 가리키게하고, 입력을 받아서 설정해준뒤,
find함수(경로압축방법 사용)를 실행시켜 각
관련 문제
https://www.acmicpc.net/problem/17352 >> https://velog.io/@cldhfleks2/17352
https://www.acmicpc.net/problem/1976 >> https://velog.io/@cldhfleks2/1976
https://www.acmicpc.net/problem/1717 >> https://velog.io/@cldhfleks2/1717
