PYTHON#27

codataffee·2024년 6월 18일
python
0

PYTHON

목록 보기
36/40
post-thumbnail

개요

분산분석

분산분석(ANOVA)은 여러 집단의 평균 차이를 통계적으로 유의미한지 검정

  • 일원 분산 분석 (One-way ANOVA) : 하나의 요인에 따라 평균의 차이 검정
  • 이원 분산 분석 (Two-way ANOVA) : 두 개의 요인에 따라 평균의 차이 검정

📌 일원 분산 분석

  • 3개 이상의 집단 간의 평균의 차이가 통계적으로 유의한지 검정

  • 하나인 요인이고, 집단의 수가 3개 이상일 때 사용

📌 기본가정

  • 독립성: 각 집단의 관측치는 독립적이다.

  • 정규성: 각 집단은 정규분포를 따른다. (샤피로 검정)

  • 등분산성: 모든 집단은 동일한 분산을 가진다. (레빈 검정)

📌 귀무가설과 대립가설

  • 귀무가설: 모든 집단의 평균은 같다.

  • 대립가설: 적어도 한 집단은 평균이 다르다.

📌 실습

  • scipy
f_oneway(sample1, sample2, ...)
  • stats
model = ols('종속변수 ~ 요인', data = df).fit()
print(anova_lm(model))

  • 프로세스

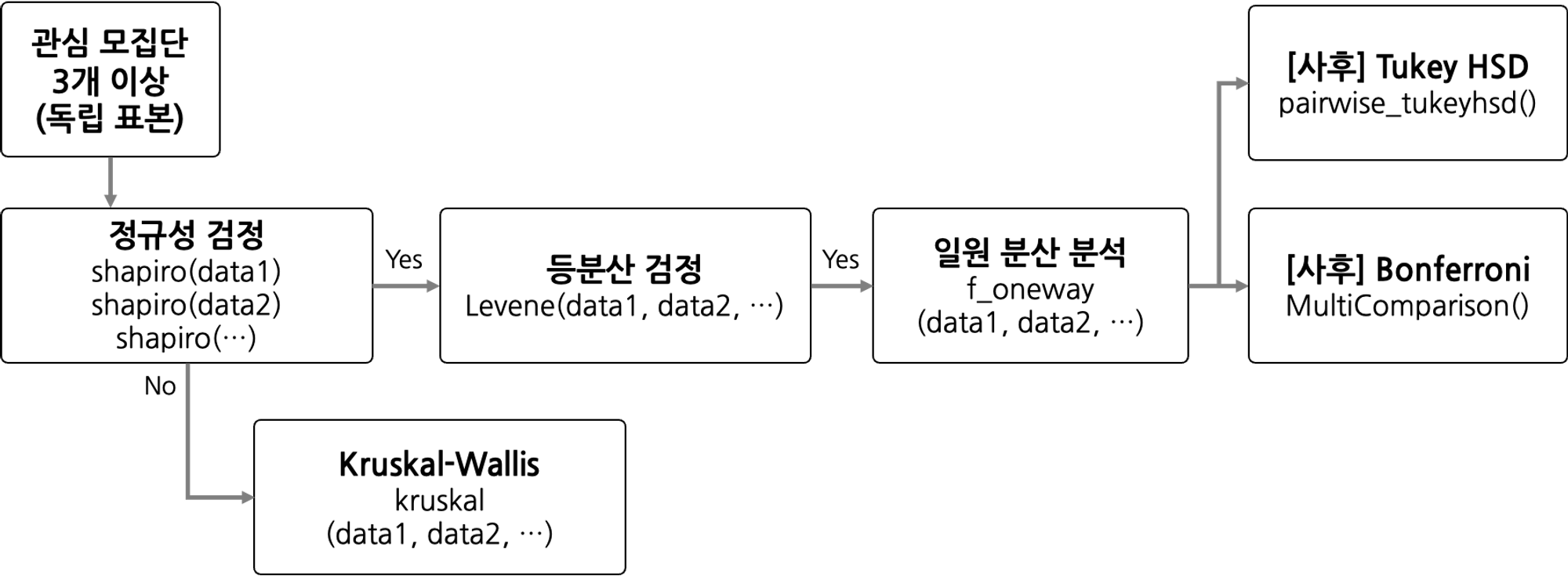
  • 사후 검정

    • 투키 (tukey)
    • 본페로니 (bonferroni) : 투키에 비해 엄격한 기준

문제

주어진 데이터는 4가지 다른 교육 방법을 적용한 대학생들의 학점 결과이다. 이 실험에서는 비슷한 실력을 가진 학생 40명을 무작위로 4개(A, B, C, D)그룹으로 나누었고, 각 그룹은 다른 교육 방법을 적용했다. 학생들의 학점 결과에는 교육 방법에 따른 차이가 있는지 유의수준 0.5하에서 검정하시오.

  • 귀무가설(H0): 네 가지 교육 방법에 의한 학생들의 학점 평균은 동일하다.
  • 대립가설(H1): 적어도 두 그룹의 학점 평균은 다르다.

import pandas as pd
df = pd.DataFrame({
    'A': [3.5, 4.3, 3.8, 3.6, 4.1, 3.2, 3.9, 4.4, 3.5, 3.3],
    'B': [3.9, 4.4, 4.1, 4.2, 4.5, 3.8, 4.2, 3.9, 4.4, 4.3],
    'C': [3.2, 3.7, 3.6, 3.9, 4.3, 4.1, 3.8, 3.5, 4.4, 4.0],
    'D': [3.8, 3.4, 3.1, 3.5, 3.6, 3.9, 3.2, 3.7, 3.3, 3.4]
})
print(df.head(2))

# 일원 분산 분석
from scipy import stats
stats.f_oneway(df['A'], df['B'], df['C'], df['D'])

# 정규성, 등분산, 일원 분산 분석
# Shapiro-Wilk(샤피로-윌크) 정규성 검정
print(stats.shapiro(df['A']))
print(stats.shapiro(df['B']))
print(stats.shapiro(df['C']))
print(stats.shapiro(df['D']))
# Levene(레빈) 등분산 검정
print(stats.levene(df['A'], df['B'], df['C'], df['D']))
# 일원 분산 분석
print(stats.f_oneway(df['A'], df['B'], df['C'], df['D']))

# 데이터 재구조화 (긴 형태)
df_melt = df.melt()
df_melt.head()

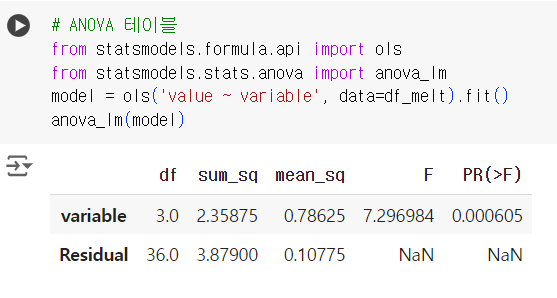
# ANOVA 테이블
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
model = ols('value ~ variable', data=df_melt).fit()
anova_lm(model)

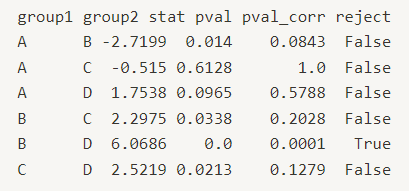
사후검정 목적 : 어떤 그룹들 간에 통계적으로 유의미한 차이가 있는지 구체적으로 파악하는 것

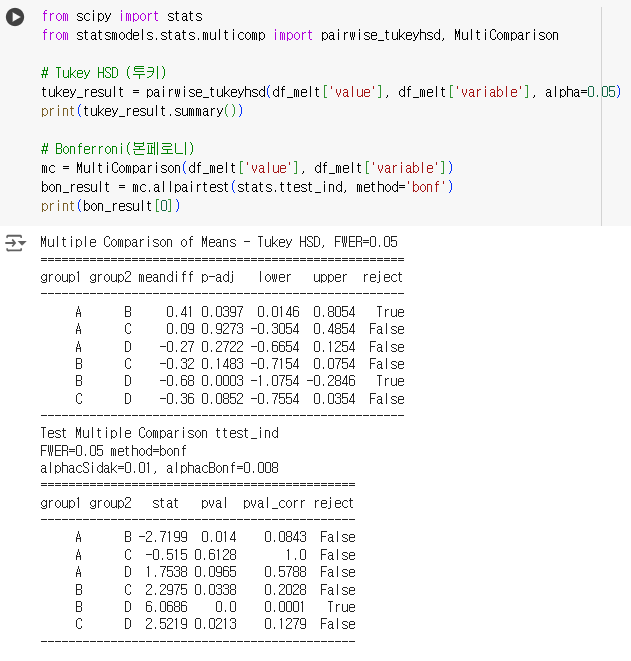
from scipy import stats
from statsmodels.stats.multicomp import pairwise_tukeyhsd, MultiComparison
# Tukey HSD (투키)
tukey_result = pairwise_tukeyhsd(df_melt['value'], df_melt['variable'], alpha=0.05)
print(tukey_result.summary())
# Bonferroni(본페로니)
mc = MultiComparison(df_melt['value'], df_melt['variable'])
bon_result = mc.allpairtest(stats.ttest_ind, method='bonf')
print(bon_result[0])

import pandas as pd
from scipy import stats
# 데이터
df = pd.DataFrame({
    'A': [10.5, 11.3, 10.8, 10.6, 11.1, 10.2, 10.9, 11.4, 10.5, 10.3],
    'B': [10.9, 11.4, 11.1, 11.2, 11.5, 10.8, 11.2, 10.9, 11.4, 11.3],
    'C': [10.2, 10.7, 10.6, 10.9, 11.3, 11.1, 10.8, 10.5, 11.4, 11.0],
    'D': [13.8, 10.4, 10.1, 10.5, 10.6, 10.9, 10.2, 10.7, 10.3, 10.4]
})
# 정규성 검정
print(stats.shapiro(df['A']))
print(stats.shapiro(df['B']))
print(stats.shapiro(df['C']))
print(stats.shapiro(df['D']))
# Kruskal-Wallis 검정
stats.kruskal(df['A'], df['B'], df['C'], df['D'])

📌 이원 분산 분석

  • 3개 이상의 집단 간의 평균의 차이가 통계적으로 유의한지 검정

  • 요인의 수가 2개, 집단의 수가 3개 이상일 때 사용

📌 기본가정

  • 독립성: 각 집단의 관측치는 독립적이다.

  • 정규성: 각 집단은 정규분포를 따른다. (샤피로 검정)

  • 등분산성: 모든 집단은 동일한 분산을 가진다. (레빈 검정)

📌 귀무가설과 대립가설

주 효과와 상호작용 효과

  • 주 효과(요인1)

    • 귀무가설: 모든 그룹의 첫 번째 요인의 평균은 동일하다.

    • 대립가설: 적어도 두 그룹은 첫 번째 요인의 평균은 다르다.

  • 주 효과(요인2)

    • 귀무가설: 모든 그룹의 두 번째 요인의 평균은 동일하다.

    • 대립가설: 적어도 두 그룹은 두 번째 요인의 평균은 다르다.

  • 상호작용효과

    • 귀무가설: 두 요인의 그룹 간에 상호작용은 없다.

    • 대립가설: 두 요인의 그룹 간에 상호작용이 있다.

📌 실습

  • stats
model = ols('종속변수 ~ C(요인1) * C(요인2)', data = df).fit()
print(anova_lm(model))
  • 프로세스

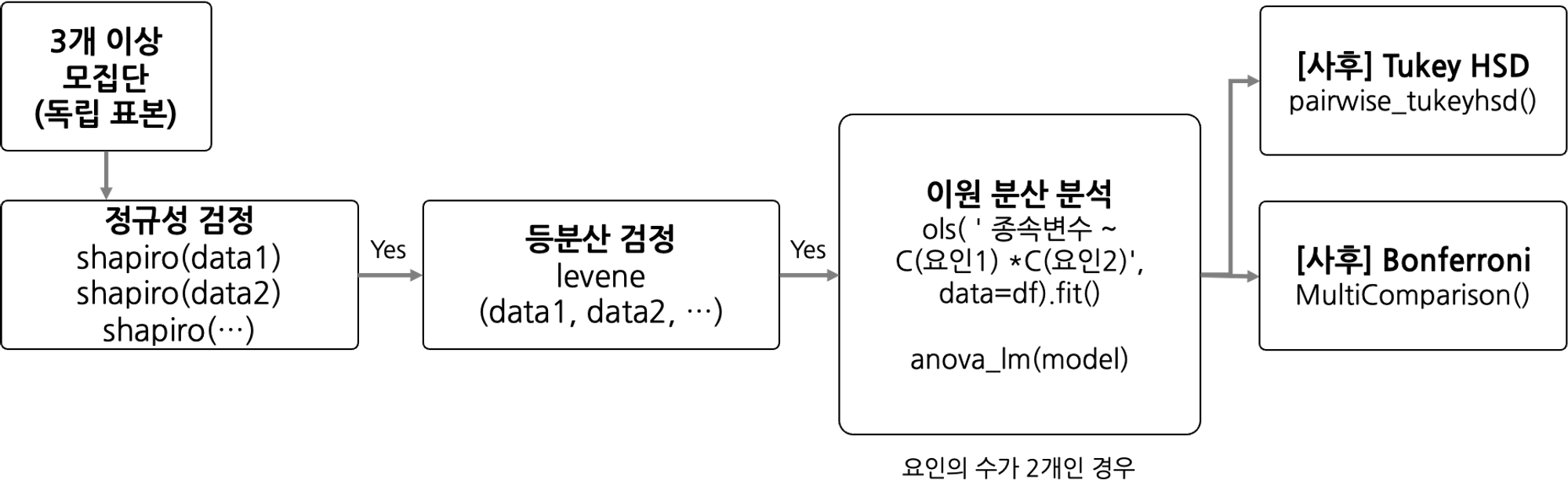
문제

가정에서 재배하고 있는 네 가지 토마토 종자(A, B, C, D)에 대해 세 가지 종류의 비료 (11, 12, 13)를 사용하여 재배된 토마토 수를 조사하였다. 종자 및 비료 종류 간의 토마토 수의 차이가 있는지 유의수준 0.05하에서 검정하시오.
(단, 정규성, 등분산성에 만족한 데이터)

  • 종자 (주 효과)
    • 귀무가설(H0): 종자 간의 토마토 수에 차이가 없다.
    • 대립가설(H1): 적어도 하나의 종자에서 토마토 수에 차이가 있다.
  • 비료 (주 효과)
    • 귀무가설(H0): 비료 종류 간의 토마토 수에 차이가 없다.
    • 대립가설(H1): 적어도 하나의 비료 종류에서 토마토 수에 차이가 있다.
  • 상호작용 효과:
    • 귀무가설(H0): 종자와 비료 간의 상호작용은 토마토 수에 영향을 미치지 않는다.
    • 대립가설(H1): 종자와 비료 간의 상호작용은 토마토 수에 영향을 미친다.

import pandas as pd
df = pd.read_csv("tomato.csv")
print(df.head())
print(df.shape)

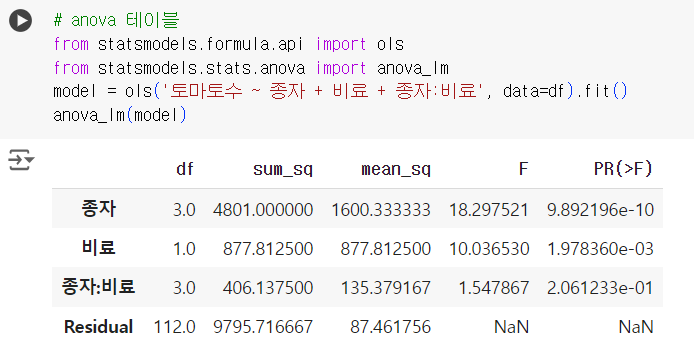
# anova 테이블
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
model = ols('토마토수 ~ 종자 + 비료 + 종자:비료', data=df).fit()
anova_lm(model)

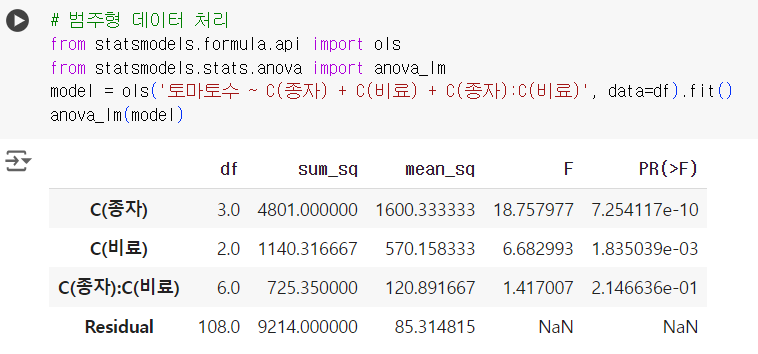
# 범주형 데이터 처리
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
model = ols('토마토수 ~ C(종자) + C(비료) + C(종자):C(비료)', data=df).fit()
anova_lm(model)

# 일반표기법 format(지수표기법, '.10f')
print(format(7.254117e-10,'.10f'))
print(format(1.835039e-03,'.10f'))
print(format(2.146636e-01,'.10f'))

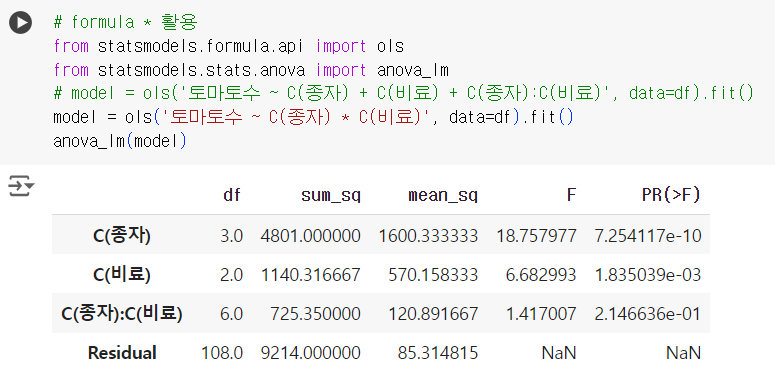
# formula * 활용
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
# model = ols('토마토수 ~ C(종자) + C(비료) + C(종자):C(비료)', data=df).fit()
model = ols('토마토수 ~ C(종자) * C(비료)', data=df).fit()
anova_lm(model)

사후검정

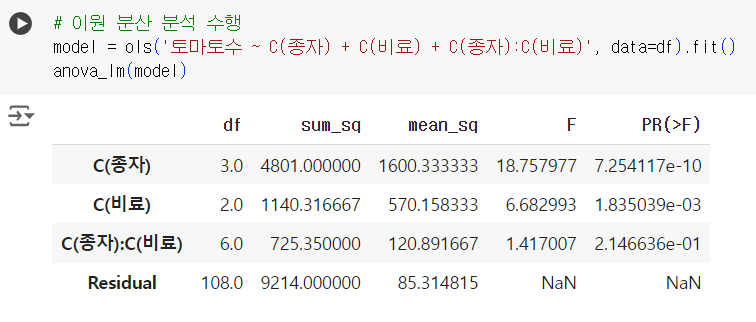
# 이원 분산 분석 수행
model = ols('토마토수 ~ C(종자) + C(비료) + C(종자):C(비료)', data=df).fit()
anova_lm(model)

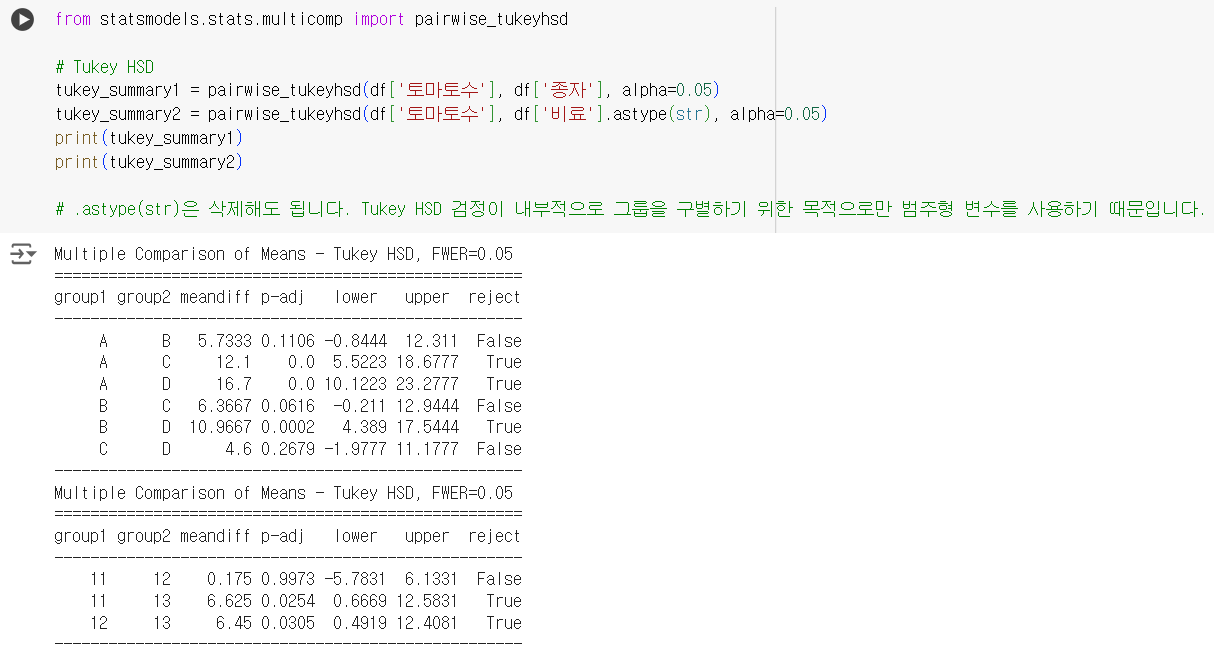
from statsmodels.stats.multicomp import pairwise_tukeyhsd
# Tukey HSD
tukey_summary1 = pairwise_tukeyhsd(df['토마토수'], df['종자'], alpha=0.05)
tukey_summary2 = pairwise_tukeyhsd(df['토마토수'], df['비료'].astype(str), alpha=0.05)
print(tukey_summary1)
print(tukey_summary2)
# .astype(str)은 삭제해도 됩니다. Tukey HSD 검정이 내부적으로 그룹을 구별하기 위한 목적으로만 범주형 변수를 사용하기 때문입니다.

# Bonferroni
from scipy import stats
from statsmodels.stats.multicomp import MultiComparison
mc = MultiComparison(df['토마토수'], df['종자'])
bon_result = mc.allpairtest(stats.ttest_ind, method="bonf", alpha=0.05)
print(bon_result[0])
mc = MultiComparison(df['토마토수'], df['비료'])
bon_result = mc.allpairtest(stats.ttest_ind, method="bonf")
print(bon_result[0])
# .astype(str)은 삭제해도 됩니다.

정규성 + 등분산

샤피로 검정을 진행하여 변수 중 1개라도 0.05보다 작다(정규성을 띄지 않는다.)면
비모수 검정을 진행해야 함.

from scipy.stats import shapiro
cond_tree_A = df['종자'] == 'A'
cond_tree_B = df['종자'] == 'B'
cond_tree_C = df['종자'] == 'C'
cond_tree_D = df['종자'] == 'D'
cond_fert_1 = df['비료'] == 11
cond_fert_2 = df['비료'] == 12
cond_fert_3 = df['비료'] == 13
print(shapiro(df[cond_tree_A & cond_fert_1]['토마토수']))
print(shapiro(df[cond_tree_A & cond_fert_2]['토마토수']))
print(shapiro(df[cond_tree_A & cond_fert_3]['토마토수']))
print(shapiro(df[cond_tree_B & cond_fert_1]['토마토수']))
print(shapiro(df[cond_tree_B & cond_fert_2]['토마토수']))
print(shapiro(df[cond_tree_B & cond_fert_3]['토마토수']))
print(shapiro(df[cond_tree_C & cond_fert_1]['토마토수']))
print(shapiro(df[cond_tree_C & cond_fert_2]['토마토수']))
print(shapiro(df[cond_tree_C & cond_fert_3]['토마토수']))
print(shapiro(df[cond_tree_D & cond_fert_1]['토마토수']))
print(shapiro(df[cond_tree_D & cond_fert_2]['토마토수']))
print(shapiro(df[cond_tree_D & cond_fert_3]['토마토수']))

레빈 검정을 진행하여 변수 중 1개라도 0.05보다 작다(등분산성을 띄지 않는다.)면
비모수 검정을 진행해야 함.

from scipy.stats import levene
print(levene(df[cond_tree_A]['토마토수'],
             df[cond_tree_B]['토마토수'],
             df[cond_tree_C]['토마토수'],
             df[cond_tree_D]['토마토수']))
print(levene(df[cond_fert_1]['토마토수'],
             df[cond_fert_2]['토마토수'],
             df[cond_fert_3]['토마토수']))

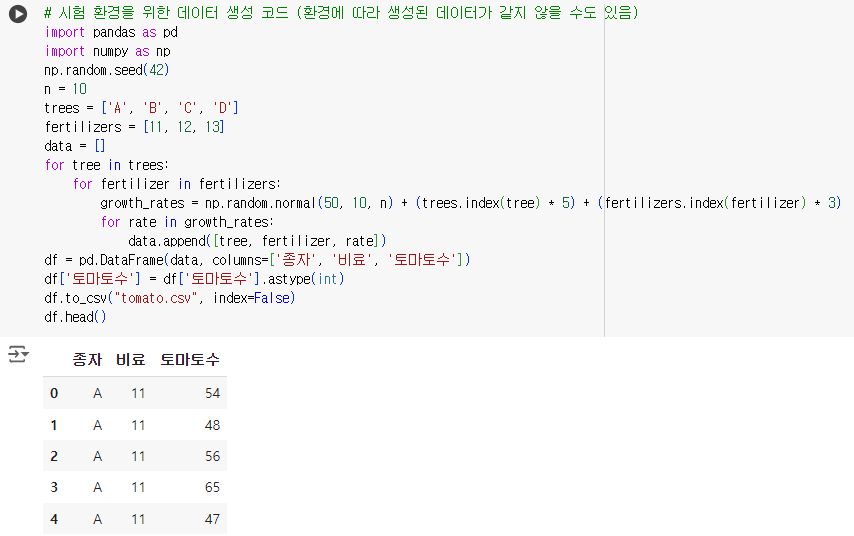
# 시험 환경을 위한 데이터 생성 코드 (환경에 따라 생성된 데이터가 같지 않을 수도 있음)
import pandas as pd
import numpy as np
np.random.seed(42)
n = 10
trees = ['A', 'B', 'C', 'D']
fertilizers = [11, 12, 13]
data = []
for tree in trees:
    for fertilizer in fertilizers:
        growth_rates = np.random.normal(50, 10, n) + (trees.index(tree) * 5) + (fertilizers.index(fertilizer) * 3)
        for rate in growth_rates:
            data.append([tree, fertilizer, rate])
df = pd.DataFrame(data, columns=['종자', '비료', '토마토수'])
df['토마토수'] = df['토마토수'].astype(int)
df.to_csv("tomato.csv", index=False)
df.head()
profile
codataffee
커피 좋아하는 데이터 꿈나무
이전 포스트

PYTHON#26

다음 포스트

PYTHON#DFS,BFS

0개의 댓글

관련 채용 정보