개요
DFS와BFS
알고리즘 코드카타(94. 타겟 넘버) 진행 중 정수 배열의 순서를 변경하지 않고 부호만 바꿔
원하는 숫자를 만들 수 있는 모든 경우를 반환하는 문제를 만났다.
재귀, for문 사용 등의 방법을 시도했지만 전혀 감이 안잡혀서 검색하던 중
깊이, 너비 우선 탐색이라는 함수 (개념)을 알게 되어 정리해본다.
📌 DFS
-
DFS (Depth-First Search) : 깊이 우선 탐색
가능한 깊이까지 탐색한 후에 다시 돌아와서 다음 경로를 탐색한다.
깊이 있는 부분을 먼저 탐색하는 함수 -
특징
-
재귀적 구현:
스택 자료 구조 사용 -
메모리 사용량:
방문한 정점과 경로를 저장하기 위해 최대 O(V)의 공간이 필요 (V ; 정점의 수) -
완전성:
모든 경로를 탐색할 수 있다. -
적용:
미로 찾기, 퍼즐 풀이, 경로 찾기 등.
-
-
구현 예시
def dfs(graph, start, visited=None):
if visited is None:
visited = set() # 방문한 노드를 저장할 집합을 초기화
visited.add(start) # 시작 노드를 방문한 것으로 표시
print(start, end=' ') # 현재 노드를 출력
for neighbor in graph[start]: # 현재 노드의 모든 이웃 노드를 순회
if neighbor not in visited: # 이웃 노드가 방문한 적이 없다면
dfs(graph, neighbor, visited) # 그 이웃 노드를 방문 (재귀 호출)
return visited # 방문한 노드 집합을 반환
# 예제 그래프 (인접 리스트)
graph = {
'A': ['B', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F'],
'D': ['B'],
'E': ['B', 'F'],
'F': ['C', 'E']
}
# DFS 호출
dfs(graph, 'A')- 탐색 세부 과정
[그래프 구조]
A
/ \
B C
/ \ \
D E F
\ /
E주어진 그래프에 DFS 함수는 다음 순서로 탐색 :
시작 노드: A
방문 순서: A
노드 A 탐색: A의 첫 번째 이웃 B를 방문
방문 순서: A, B
노드 B 탐색: B의 첫 번째 이웃 A는 이미 방문했으므로, 다음 이웃 D를 방문
방문 순서: A, B, D
노드 D 탐색: D의 이웃 B는 이미 방문했으므로, 더 이상 탐색할 노드가 없음. D에서 돌아옴.
방문 순서: A, B, D
노드 B 탐색 재개: B의 다음 이웃 E를 방문
방문 순서: A, B, D, E
노드 E 탐색: E의 첫 번째 이웃 B는 이미 방문했으므로, 다음 이웃 F를 방문
방문 순서: A, B, D, E, F
노드 F 탐색: F의 첫 번째 이웃 C를 방문
방문 순서: A, B, D, E, F, C
노드 C 탐색: C의 첫 번째 이웃 A는 이미 방문, 다음 이웃 F도 이미 방문,
더 이상 탐색할 노드가 없음. C에서 돌아옴.
방문 순서: A, B, D, E, F, C
** 전체 탐색 결과
DFS 탐색 결과는 A B D E F C
📌 BFS
-
BFS (Breadth-First Search): 너비 우선 탐색
현재 정점의 모든 인접 정점을 먼저 탐색한 후 다음 정점으로 이동
같은 깊이의 모든 정점을 탐색하는 함수 -
특징
-
반복적 구현:
큐 자료 구조 사용 -
메모리 사용량:
방문한 정점과 경로를 저장하기 위해 최대 O(V)의 공간 필요 (V ; 정점의 수) -
최단 경로:
BFS는 무향 그래프에서 최단 경로를 찾는 데 사용 -
적용:
최단 경로 찾기, 레벨 오더 트리 탐색 등.
-
-
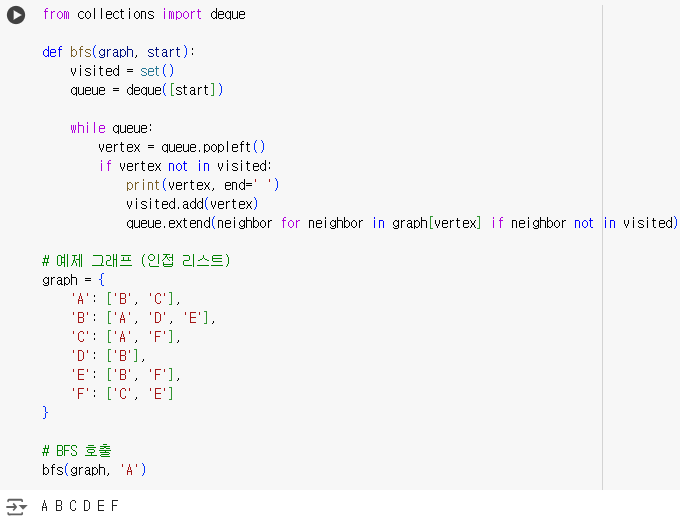
구현 예시
from collections import deque
def bfs(graph, start):
visited = set() # 방문한 노드를 저장할 집합
queue = deque([start]) # 시작 노드를 큐에 추가
while queue: # 큐가 비어있지 않은 동안 반복
vertex = queue.popleft() # 큐의 맨 앞 노드를 꺼냄
if vertex not in visited: # 해당 노드가 방문한 적이 없다면
print(vertex, end=' ') # 노드를 출력
visited.add(vertex) # 노드를 방문한 것으로 표시
# 해당 노드의 이웃 노드를 큐에 추가 (아직 방문하지 않은 노드만)
queue.extend(neighbor for neighbor in graph[vertex] if neighbor not in visited)
# 예제 그래프 (인접 리스트)
graph = {
'A': ['B', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F'],
'D': ['B'],
'E': ['B', 'F'],
'F': ['C', 'E']
}
# BFS 호출
bfs(graph, 'A')- 탐색 세부 과정
[그래프 구조]
A
/ \
B C
/ \ \
D E F
\ /
E
BFS 탐색 순서
시작 노드: A
큐: ['A']
방문 순서: A
노드 A 탐색: A의 이웃 B와 C를 큐에 추가
큐: ['B', 'C']
방문 순서: A
노드 B 탐색: B의 이웃 A, D, E를 큐에 추가 (A는 이미 방문)
큐: ['C', 'D', 'E']
방문 순서: A, B
노드 C 탐색: C의 이웃 A, F를 큐에 추가 (A는 이미 방문)
큐: ['D', 'E', 'F']
방문 순서: A, B, C
노드 D 탐색: D의 이웃 B를 큐에 추가 (B는 이미 방문)
큐: ['E', 'F']
방문 순서: A, B, C, D
노드 E 탐색: E의 이웃 B, F를 큐에 추가 (B는 이미 방문, F는 이미 큐에 존재)
큐: ['F']
방문 순서: A, B, C, D, E
노드 F 탐색: F의 이웃 C, E를 큐에 추가 (C와 E는 이미 방문)
큐: []
방문 순서: A, B, C, D, E, F
** 전체 탐색 결과
BFS 탐색 결과는 A B C D E F
📌 DFS & BFS 비교
-
탐색 순서:
DFS는 깊이를 우선으로 탐색, BFS는 너비를 우선으로 탐색. -
경로 탐색:
DFS는 특정 경로를 찾기 좋음, BFS는 최단 경로를 찾기 좋음. -
구현:
DFS는 재귀나 스택으로 구현, BFS는 큐로 구현. -
메모리 사용:
그래프의 형태와 탐색 경로에 따라 다르지만,
일반적으로 BFS가 더 많은 메모리를 사용할 수 있다.