개요
<통계학>
데이터 분석 및 과학을 위한 핵심 통계지식 학습
PYTHON 활용 :
통계적 가설검증,회귀(예측),분류(지도학습),클러스터링(비지도학습)에 대한 이해
📌 3회차 요약
-
회귀분석은
독립변수와종속변수가 나누어진 (또는 나눌 수 있는) 데이터를 기반으로 진행독립변수: 원인종속변수: 결과
-
회귀분석은 크게 3단계로 진행
- 독립변수, 종속변수 설정
- 데이터 경향성 확인
- 정합성 검증 & 결과 해석
-
회귀분석의 결과해석은 회귀식이 얼마나
설명력을 가지는지, 회귀식이통계적으로 유의한지, 독립변수와 종속변수 간상관관계가 유의미한지 확인 -
각각의 검정통계량(t-value, F-value)이 가지는 숫자의 의미보다,
이를 신뢰할 수 있는지(p-value)에 포커스 !
📌 회귀 분석
📌 이해하기
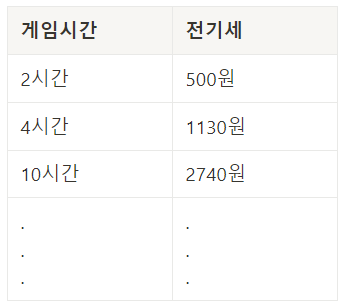
게임 시간과 전기세에 대한 데이터가 있다고 가정
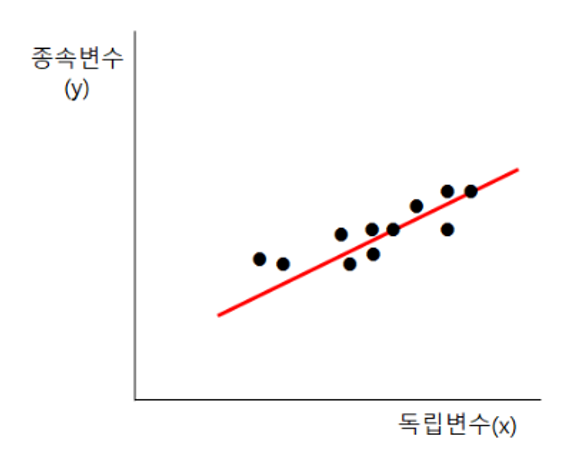
그래프의 X 축은
독립 변수, Y 축은종속 변수를 의미하고, 점들은 각 데이터를 의미
독립 변수는 원인이 되는 변수를 의미, 여기서는 게임 시간
종속 변수는 결과가 되는 변수를 의미, 여기서는 전기세
만약 게임 시간이 1000 시간일 경우, 전기세는 얼마일까?
- 우리가 가진 데이터셋에 해당하는 값이 없을 때,
이를 예측하기 위해 회귀분석의 개념 도입,
예측을 위해 위 그래프에서 보이는 빨간 선 (추세선)이 필요한데,
회귀분석의 목적이 추세선을 찾는 것
추세선
= 이미 가지고 있는 데이터를 가장 잘 설명해주는 선
= Y = A + BX (방정식)
X : 게임 시간 (독립변수)
Y : 전기세 (종속변수)
A : 절편 (X가 0일 때 Y 값)
B : 기울기 (가중치)📌 요약
✅ 역사
통계학에서 회귀 라는 용어는 1889년 프란시스 갈튼이 특정 현상을 설명하기 위해
평균으로의 회귀 라는 용어를 사용하면서 시작
✅ 정의
독립변수 (X)로 종속변수 (Y) 를 예측하는 분석 기법
독립변수 : 원인 변수, 설명 변수 / 종속변수 : 결과 변수, 반응 변수
✅ 프로세스
-
독립변수, 종속변수 설정
독립변수와 종속변수를 정하고 가설을 설정한다.- 독립변수 : 게임 시간 / 종속변수 : 전기세
- 귀무가설 : 게임 시간은 전기세와 관련이 없을 것이다.
- 대립가설 : 게임 시간은 전기세와 관련이 있을 것이다.
-
데이터 경향성 확인
독립변수와 종속변수 간 산점도 분석 및 상관관계 분석을 통해 데이터 분포 확인 -
정합성 검증 & 결과 해석
- 회귀모델(회귀식)이 얼마나 설명력을 갖는가
- 회귀모델(회귀식)이 통계적으로 유의한가
- 독립변수와 종속변수 간 선형관계가 있는가
📌 특징
장점
- 친밀성
예측문제 해결에서 가장 많이 사용되고 있는 방법으로 분석 및 해석방법이 많이 있다. - 유용성
결과에 대한 근거, 이유, 활용 방안 등의 정보를 얻는 데 유용하다. - 유연성
종속 변수를 설명하기 위한 다양한 독립변수를 선택하고 실험할 수 있다.
단점
- 복잡성
기본 가정이 어긋나면 회귀분석이 불가능하다. - 한계성
비선형성 확인을 위한 적절한 방식이 존재하지 않는다.
📌 종류
회귀분석은 회귀 계수의 선형 여부, 독립변수의 갯수, 종속변수의 갯수에 따라
여러가지 유형으로 나눌 수 있는데,
데이터 분석에서 가장 많이 사용되는 회귀분석은
선형 회귀분석 과 로지스틱 회귀분석이 있다.
-
선형 회귀분석- 독립변수 : 연속형
- 종속변수 : 연속형
- 분석 목적 : 예측
- 분석 방법 : 선형 방정식에 의한 함수식 표현
-
종류
-
단순 회귀 : 독립변수 1개, 종속변수 1개
방정식 :
→ : 예측된 회귀선
→ : y절편
→ : 회귀 계수(slope, 기울기) - 설명변수 X의 변화에 따라 반응변수 y가 반응하는 정도
→ : 오차 (추론통계에서는 항상 오차가 있다) -
다중 회귀 : 독립변수 2개 이상, 종속변수 1개
방정식 :
-
-
예시
공부시간(독립변수)에 따른 시험점수(종속변수)
치킨 판매량(독립변수)에 따른 맥주 판매량(종속변수)
스트레스 수치(독립변수)에 따른 질환 수치(종속변수)
-
로지스틱 회귀분석- 독립변수 : 연속형, 범주형
- 종속변수 :
이진 (범주형이면서 이진형 ; 예/아니오, 0/1, 앞/뒤 등)
다항 (순서가 없는 범주형) - 분석 목적 : 분류, 예측
- 분석 방법 : 연결 함수를 이용한 함수식 표현
-
종류
- 이진 로지스틱 회귀 : 종속 변수가 두 가지 중 하나의 값을 가지는 경우
- 다중 로지스틱 회귀 : 종속 변수가 순서가 없는 3개 이상일 경우
-
예시
공부시간(독립변수)에 따른 시험합격여부(종속변수) ; 이진 로지스틱
비행시간(독립변수)에 따른 여행국가(종속변수) ; 다중 로지스틱
📌 정합성 검증 & 결과 해석
회귀모델의 설명력
- 회귀모델 (회귀식)이 얼마나 설명력을 갖는가?
- 결정계수 R-squared (R²) 확인
결정계수는 종속변수와 독립변수의 관계를 나타내는 수치
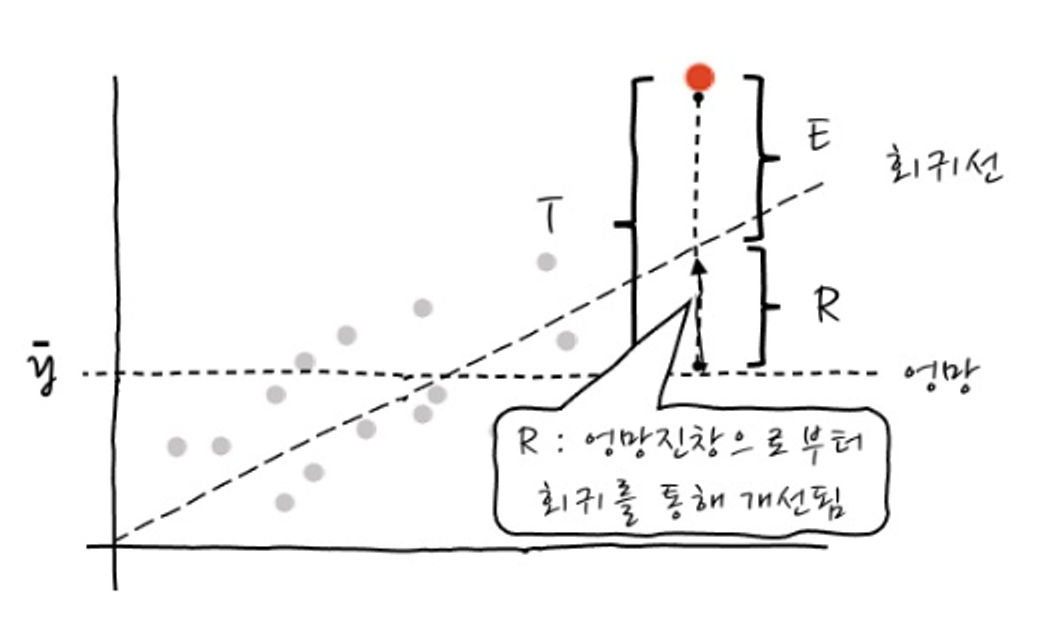
- 결정계수 R-squared (R²) 확인
T: Total = 전체 변동
R: Regression = 회귀분석을 통해 찾아낸 회귀선까지의 변동
E: Error = 잔차 = 회귀로 설명할 수 없는 변동
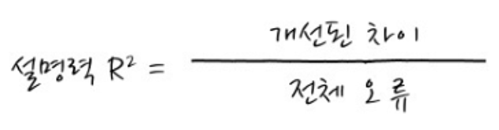
- 설명력 (R²) 은 전체 오류 중 회귀를 통해 얼마나 개선되었는가를 의미
0 과 1 사이의 값을 가지며, 1에 가까울수록 모델의 성능이 좋다는 것을 의미
회귀모델의 유의성
- 회귀모델 (회귀식)이 통계적으로 유의한가?
- 회귀식에 대한 F 검정 시행
→ 귀무가설 : 회귀모델은 타당하지 않을 것이다.
→ 대립가설 : 회귀모델은 타탕할 것이다.
→ p-value로 유의성을 판단
- 회귀식에 대한 F 검정 시행
F-검정을 통해 얻은 p-value 값이 0.05보다 작다면 대립가설 채택 (신뢰도95%)
p-value는신뢰도에 대한 검정통계량 !
변수 간 선형관계
- 독립변수와 종속변수 간 선형관계가 있는가?
- 회귀식의 가중치(기울기)에 대한 t 검정 시행
→ 귀무가설: 독립변수와 종속변수 간 선형적인 연관이 없을 것이다.
→ 대립가설: 독립변수와 종속변수 간 선형적인 연관이 있을 것이다.
→ p-value로 유의성을 판단
- 회귀식의 가중치(기울기)에 대한 t 검정 시행
t-검정을 통해 얻은 p-value 값이 0.05보다 작다면 대립가설 채택
OLS 해석
- OLS(Ordinary Least Squares) 해석하기
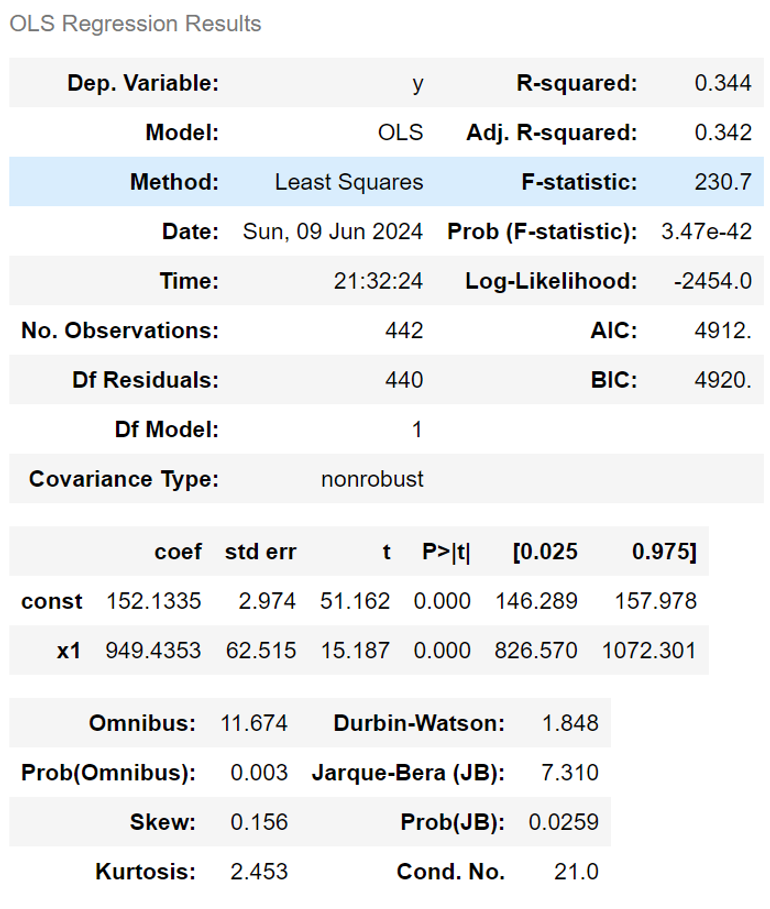
OLS 는 선형 회귀 모델의 결과를 나타내는 회귀 결과표
summary라는 함수를 활용해 아래의 결과표를 얻을 수 있다.
- Dep. Variable (종속 변수) : 회귀 모델에서 사용된 종속 변수를 표시
- Model : 회귀 모델의 종류. 여기서는 OLS (최소제곱법) 회귀 모델 사용
- OLS : 근사적으로 구하려는 해와 실제 해의 오차의 제곱의 합이 최소가 되는 해를 구하는 방법
- Method : 회귀 분석에 사용된 메소드. 여기서는 Least Squares (최소제곱법)사용
- Date : 회귀 분석이 수행된 날짜
- Time : 회귀 분석이 수행된 시간
- No. Observations : 사용된 샘플의 수 (관측치의 개수)
- coef: 회귀 계수
- std err (표준 오차) : 회귀 계수의 표준 오차
- t-statistic (t-통계량) : 회귀 계수에 대한 t-통계량.
- P>|t| (p-value) : 각 계수에 대한 p-value
- [0.025 0.975] : 95% 신뢰구간 의미
- R-squared (결정 계수) : 회귀모델의 설명력. 1에 가까울수록 모델이 데이터를 잘 설명하고 있다는 것을 의미
- F-statistic (F-통계량) : 모델 전체의 통계적 유의성을 나타내는 F-통계량이다. 높을수록 모델이 통계적으로 유의미하다는 것을 의미
- Prob (F-statistic) : F-통계량에 대한 p-value
📌 실습
import pandas as pd import numpy as np # 데이터 분포 확인을 위한 plt 라이브러리 import import matplotlib.pyplot as plt #sklearn 에서 제공하는 데이터 셋 중 하나인 diabetes 불러오기 from sklearn.datasets import load_diabetes #회귀분석 라이브러리 import from sklearn.linear_model import LinearRegression lr = LinearRegression() from PIL import Image
# 데이터 불러오기 df = load_diabetes()
# 데이터는 dictionary 형태로 저장되어 있기 때문에 keys() 를 통해 어떤 데이터를 가지고 있는지 확인 # target은 당뇨병의 수치 df.keys()
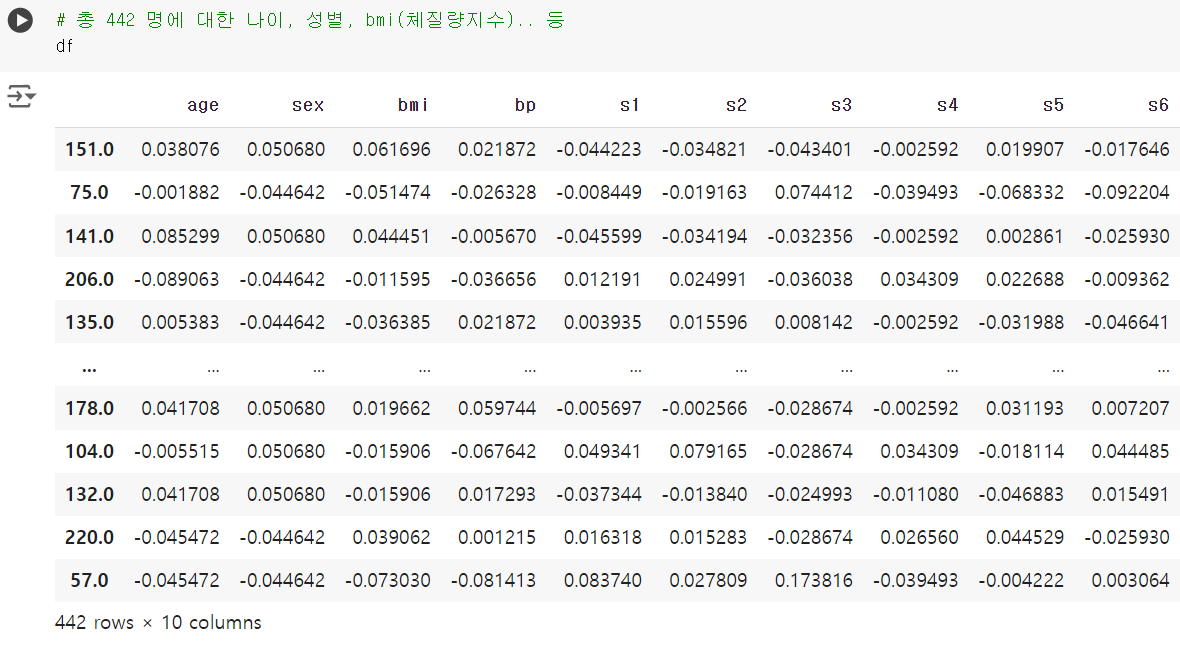
# 각각의 데이터를 가져와 dataframe 으로 받기 df = pd.DataFrame(df['data'],index=df['target'], columns=df['feature_names'])
# 단순선형회귀분석 # 당뇨병의 수치(target)와 bmi(체질량지수) 간 회귀분석 시행 # 종속변수: 당뇨병수치 # 독립변수: bmi(체질량지수) Y = df.index.values X = df.bmi.values
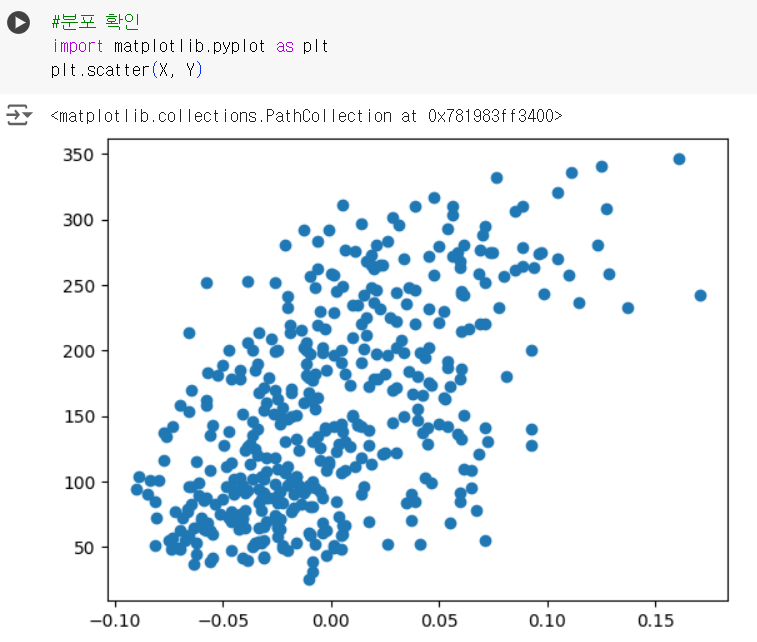
#분포 확인 import matplotlib.pyplot as plt plt.scatter(X, Y)
# 회귀분석을 위한 2d array로 변환 X = X.reshape(-1,1) Y = Y.reshape(-1,1)
+) Numpy 배열 재구성 : reshape()
- reshape 메서드는 배열의 형태(차원)을 변경하는데, 1차원 배열을 2차원 배열로 바꾸거나, 2차원 배열의 형태를 변경할 수 있다.
- 동작 원리 :
-1은 Numpy에게 배열의 길이를 알아서 계산하도록 지시하는 특수한 값.
다른 차원의 크기를 지정하면 나머지 차원의 크기는 자동으로 결정된다.(a, b)형태로 지정하면a행과b열로 배열을 재구성한다.
- 많은 머신 러닝 라이브러리는 입력 데이터가 2차원 배열로 제공되어야 작동한다.
각 행은 하나의 데이터 포인트를 나타내고, 각 열은 데이터 포인트의 특징을 나타낸다.
+)LinearRegression모델의fit()메서드에 1차원 배열을 입력하면 오류가 발생한다. - 회귀분석을 위해 2차원 배열로 변환
# 원본 배열 (1차원) import numpy as np X = np.array([1, 2, 3, 4, 5]) Y = np.array([2, 4, 6, 8, 10]) # 2차원 배열로 변환 X = X.reshape(-1, 1) Y = Y.reshape(-1, 1) # 변환 결과 X: [[1] [2] [3] [4] [5]] Y: [[ 2] [ 4] [ 6] [ 8] [10]]
# 회귀분석 시행 # 회귀계수를 확인하고 회귀식을 도출 # y= b0 +b1x # b0, b1 lr.fit(X, Y).intercept_, lr.fit(X, Y).coef_[0] 회귀식: y= 152.133 + 949.435*x
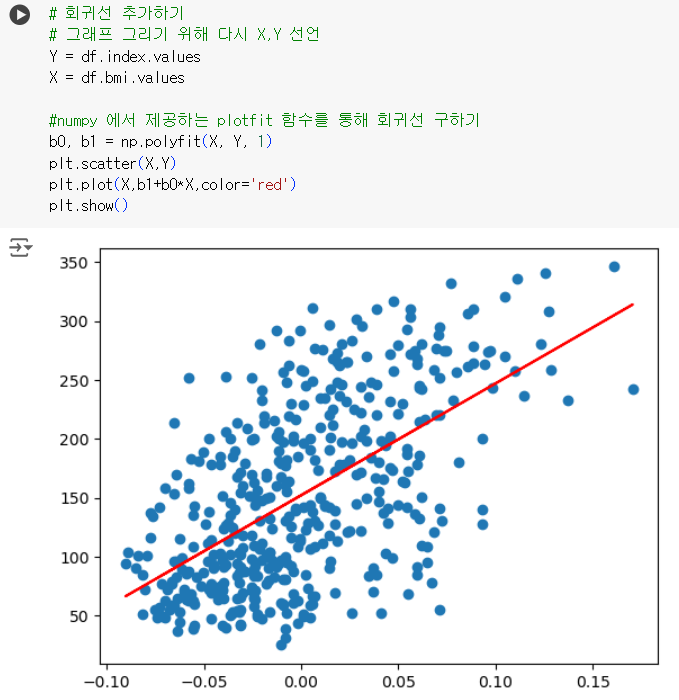
# 회귀선 추가하기 # 그래프 그리기 위해 다시 X,Y 선언 Y = df.index.values X = df.bmi.values #numpy 에서 제공하는 plotfit 함수를 통해 회귀선 구하기 b0, b1 = np.polyfit(X, Y, 1) plt.scatter(X,Y) plt.plot(X,b1+b0*X,color='red') plt.show()
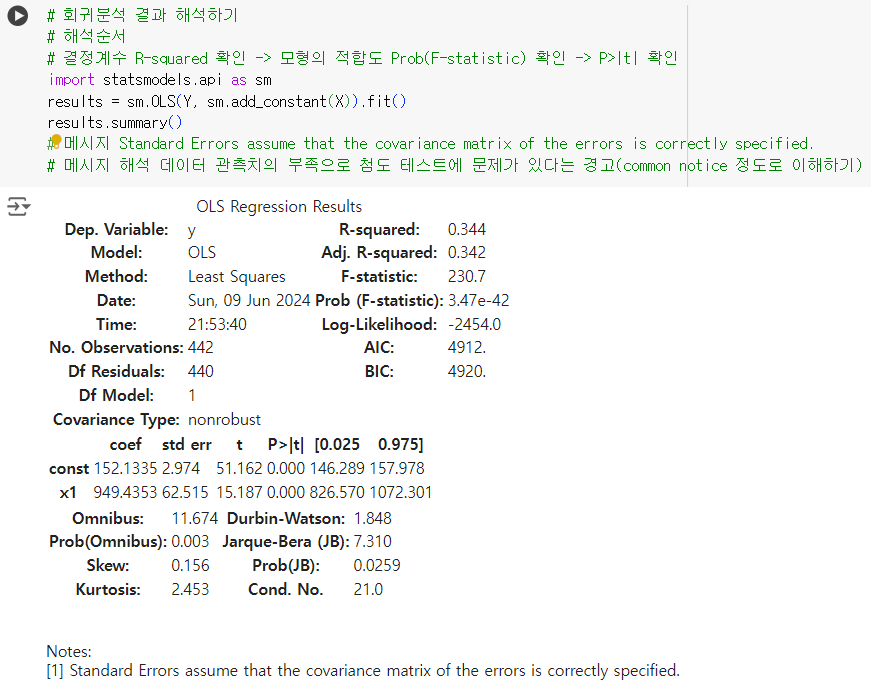
# 회귀분석 결과 해석하기 # 해석순서 # 결정계수 R-squared 확인 -> 모형의 적합도 Prob(F-statistic) 확인 -> P>|t| 확인 import statsmodels.api as sm results = sm.OLS(Y, sm.add_constant(X)).fit() results.summary() # 메시지 Standard Errors assume that the covariance matrix of the errors is correctly specified. # 메시지 해석 데이터 관측치의 부족으로 첨도 테스트에 문제가 있다는 경고(common notice 정도로 이해하기)
-
R-squared
값이 0.34... 로 이는 34% 만큼의 설명력을 가진다고 판단할 수 있다.
0에 가까울 수록 예측값을 믿을 수 없고 1에 가까울 수록 믿을 수 있다고 판단# R-squared 결정 계수 값은 1에 가까울수록 좋지만 보통 높으면 0.6 / 평균 0.3 ~ 0.4 가 나온다. 너무 높게 나오면 잘못된 결과일 확률이 높다. -
Prob(F-statistic)
도출된 회귀식이 회귀분석 모델 전체에 대해 통계적으로 의미가 있는지 파악# F - statistic의 p-value 값은 Prob(F-statistic)으로 표현되는데, Prob(F-statistic) 값이 3.47e-42로 0.05보다 작기 때문에 이 회귀식은 회귀분석 모델 전체에 대해 통계적으로 의미가 있다고 볼 수 있다. -
P > |t|
각 변수가 종속변수에 미치는 영향이 유의한지 파악# x1에 대한 p-value가 0.000으로 표기 되어 있기 때문에 0.05보다 작으므로 target을 설명하는데 유의하다고 볼 수 있다.