TIL(24.06.11.)

---

#INTRO

오..ㅋㅋ 500시간

실력도 500시간 만큼 올랐으면 좋겠다.

---

#코드카타 (09:00 ~ 10:00)

• KATA #59

• PYTHON

  • H - Index

    # 논문의 인용 횟수 배열을 이용해 조건에 해당하는 최댓값 찾기
    # 1. 주어진 논문의 인용 횟수 배열을 내림차순으로 정렬  
    # 2. 정렬된 배열에서 각 논문이 인용된 횟수를 확인하며 h 값 계산
    # 3. 논문의 인용 횟수가 논문의 순서(1-based index)와 같거나 클 때의 최댓값 찾기
    def solution(citations):
        # 논문의 인용 횟수를 내림차순으로 정렬
        citations.sort(reverse=True)
      
        # 각 논문의 인용 횟수와 순서를 비교하여 H-Index 계산
        h = 0
        for i in range(len(citations)):
            if citations[i] >= i + 1:
                h = i + 1
            else:
                break
     
        return h

  • 코드 실행 과정 :

    # 주어진 배열 [3, 0, 6, 1, 5]를 내림차순으로 정렬하면 [6, 5, 3, 1, 0]이 된다.
    각 논문의 인용 횟수와 순서를 비교 :
    인덱스 0 (순서 1): 6 >= 1 -> h = 1  
    인덱스 1 (순서 2): 5 >= 2 -> h = 2
    인덱스 2 (순서 3): 3 >= 3 -> h = 3
    인덱스 3 (순서 4): 1 < 4 -> 조건 불만족, 여기서 멈춤
    최종 h 값은 3

---

#빅분기 실기 개념 복습 (10:00 ~ 14:00)

• 가설검정 과정 및 방법 > PYTHON#23
  

---

#통계학 세션 수강 (14:00 ~ 16:00)

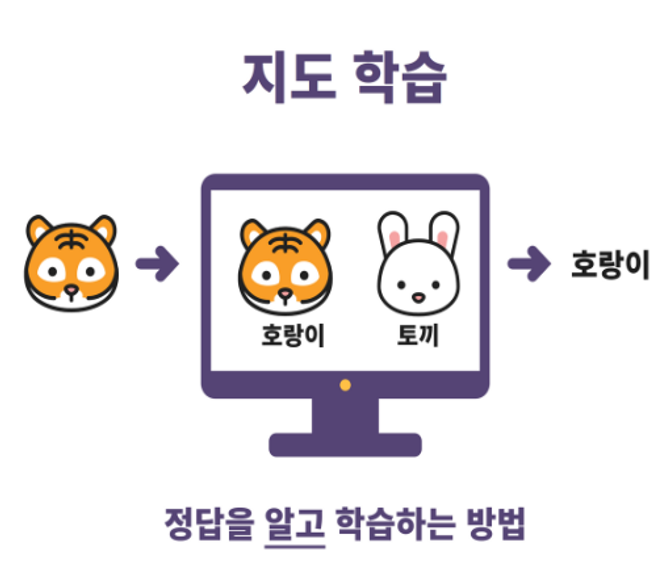
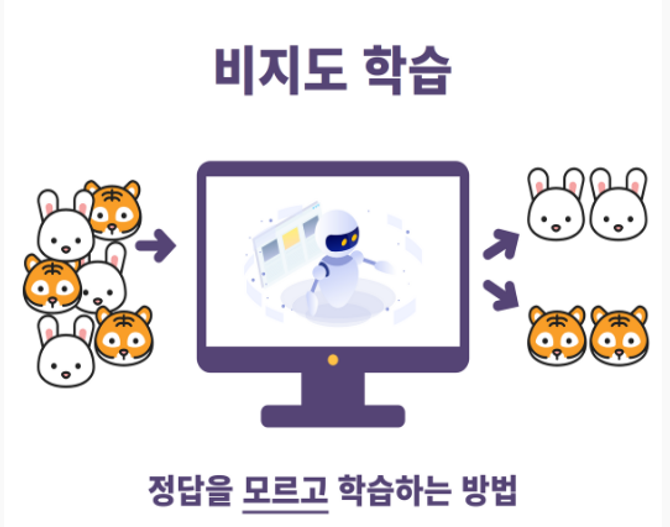
• 지도학습 & 비지도학습 > STATISTICS#4
  

---

#빅분기 실기 실습 (17:00 ~ 21:00)

• 단일 / 대응 / 독립 표본 검정 실습 > PYTHON#24

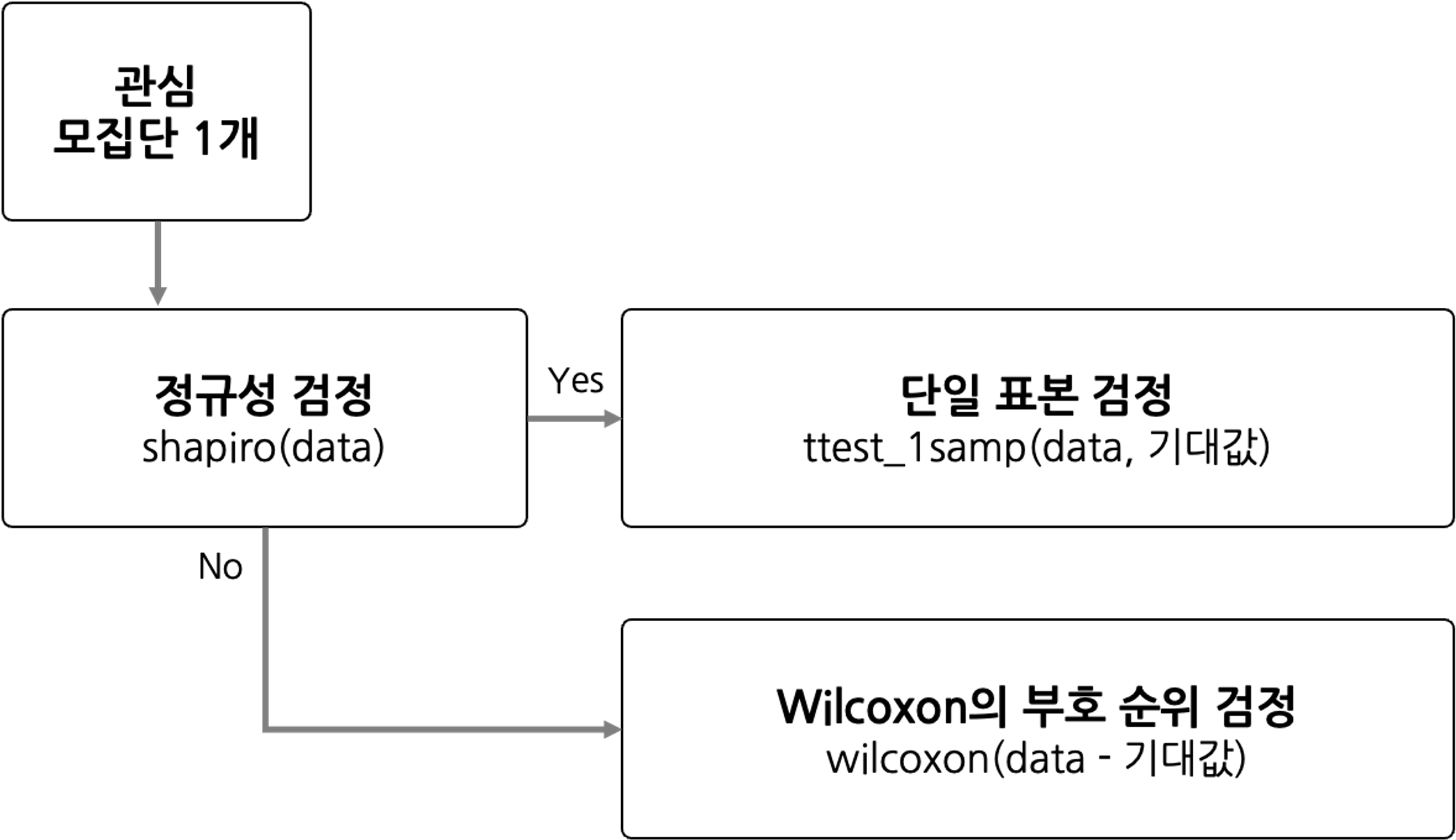
• 단일 표본 검정
  모집단이 1개일 경우, 한 그룹에 대한 검정 프로세스
  stats.shapiro(data) : 샤피로 검정
  ttest_1samp(data, 기댓값) : 단일 표본 검정
  wilcoxon(data - 기댓값) : 윌콕슨 검정

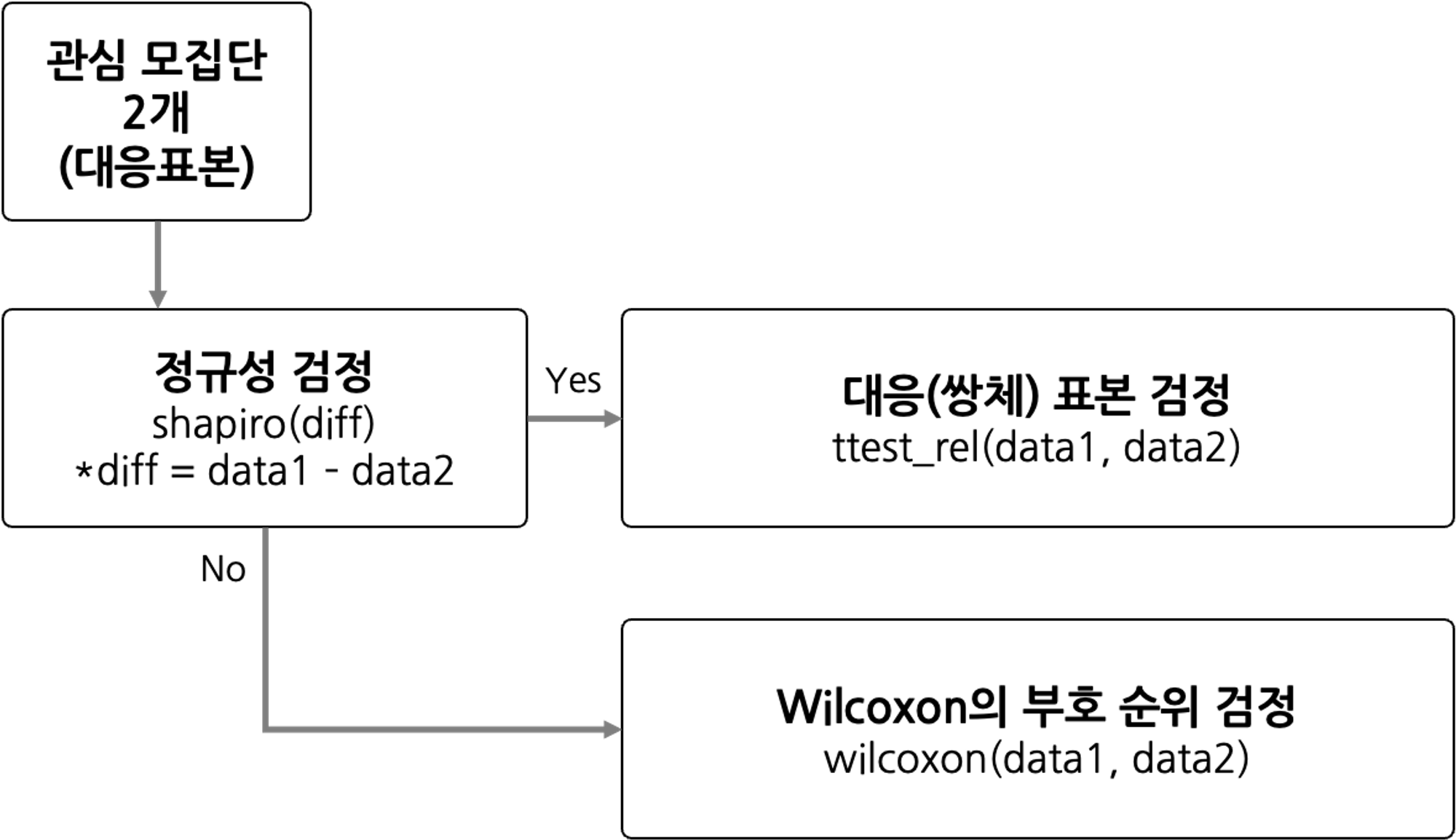
• 대응 표본 검정
  모집단이 2개일 경우, 같은 그룹에 대한 검정 프로세스
  stats.shapiro(diff) : 샤피로 검정
  ttest_rel(data1, data2) : 대응 표본 검정
  wilcoxon(data1, data2) : 윌콕슨 검정

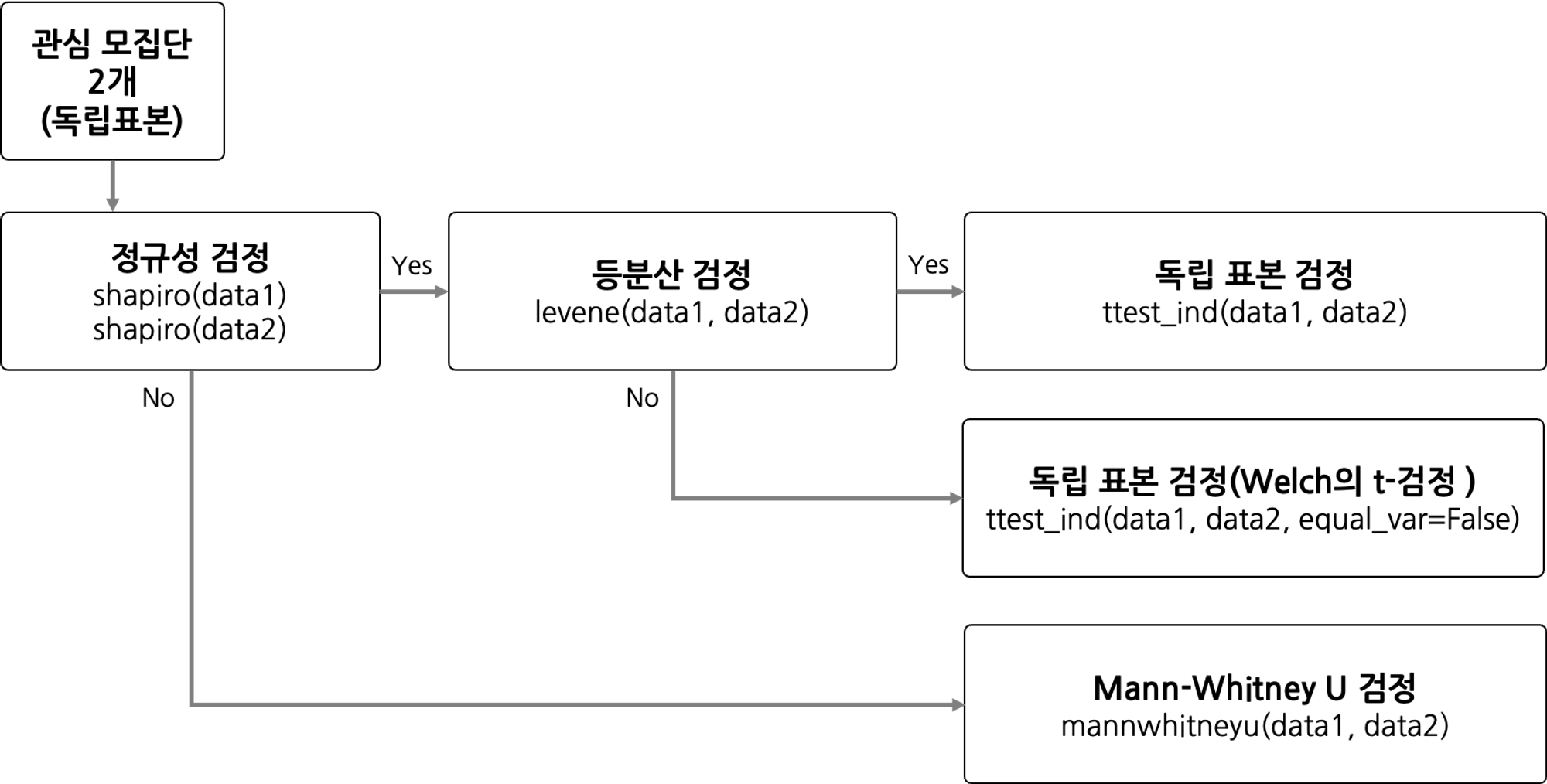
• 독립 표본 검정
  모집단이 2개일 경우, 서로 다른 그룹에 대한 검정 프로세스
  stats.shapiro(data1) , stats.shapiro(data2) : 샤피로 검정
  levene(data1, data2) : 레빈 검정
  ttest_ind(data1, data2) : 독립 표본 검정
  ttest_ind(data1, data2, equal_var = False) : 독립 표본 검정 (등분산성 X)
  mannwhitneyu(data1, data2) : 만휘트니유 검정

---

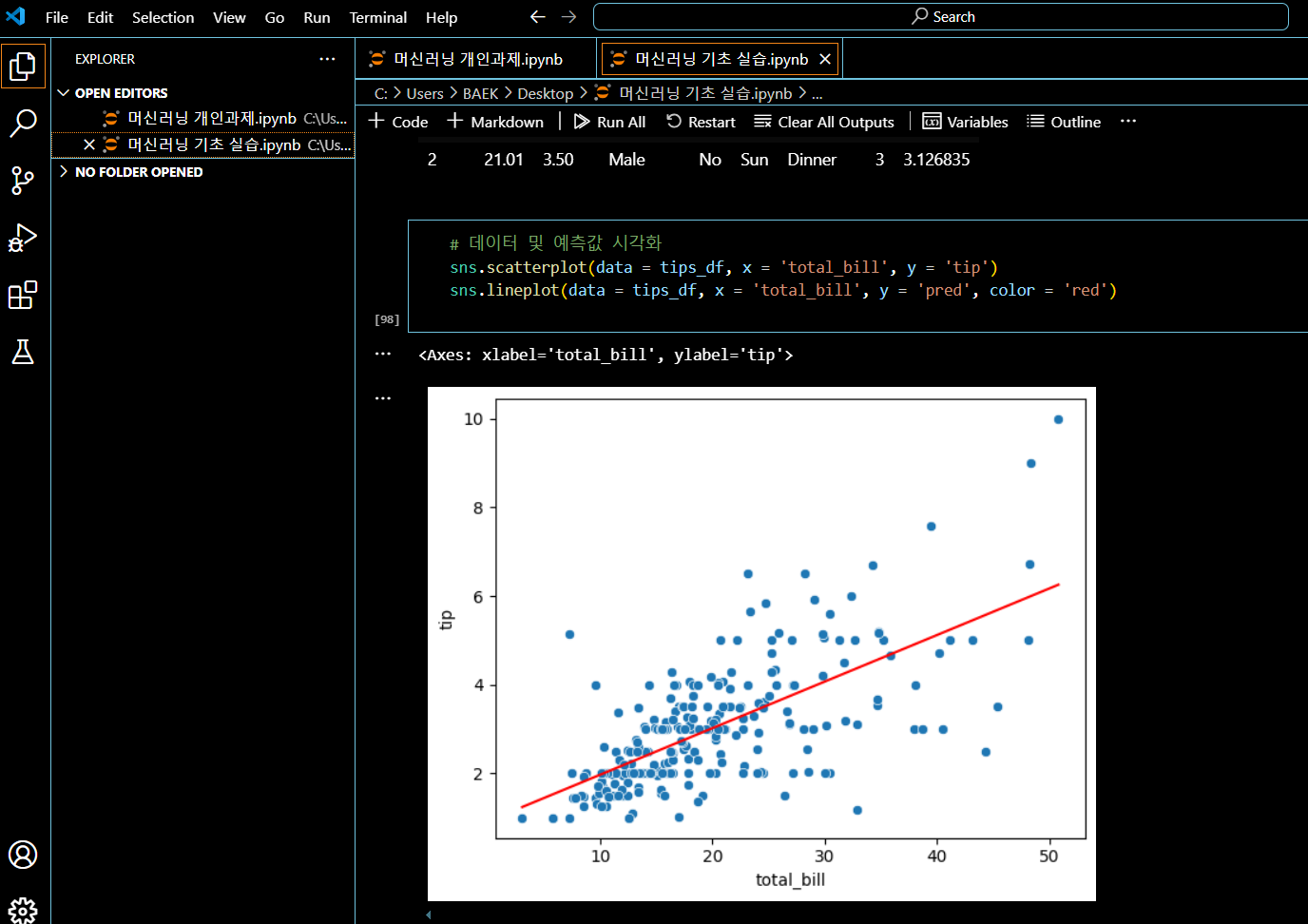
#머신러닝 기초 실습 복습 (21:00 ~ 23:00)

• 과제 풀이와 함께 실습 복습 !

  

---

#OUTRO

오늘의 한 줄.

오늘 집중이 좀 잘된 것 같은데 ?