batch normalization은 hyperparameter를 찾는 문제를 더 쉽게 만들어주고 nerual network가 hyperparameter를 선택할 때에 더욱 robust할 수 있게 해준다.

Batch / Mini-Batch

전체 train example m개를 vectorize한 것을 batch라고 부른다.
하지만 m=5000000처럼 매우 크다면 이를 한번에 training하기가 어려워지기 때문에 이 train sample을 일정하게 쪼개서 사용하게 된다. training sample을 쪼갠 것이 mini-batch이다.

m=5000000이라면 1000개의 sample을 가진 5000개의 mini-batch로 나눌 수 있다.

5백만개의 gradient를 다 구해서 average를 구하는 것은 메모리와 속도 issue가 있기 때문에 mini-batch를 사용해서 mini-batch단위로 gradient를 구한 뒤 그 gradient들의 평균을 이용하게 된다. 5백만개의 gradient로 1번 딱 이동하는 것과 5백만개를 쪼개서 mini-batch로 500번을 조금씩 이동하는 것의 차이이다.
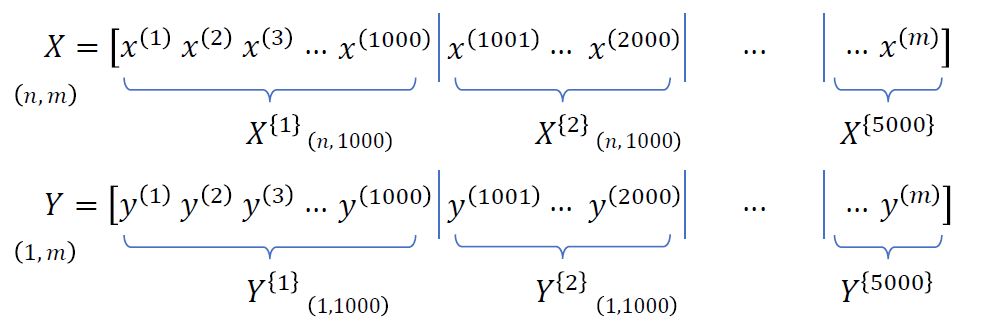mini-batch의 표기는 X{t}, Y{t}와 같이 {} 를 사용한다.

mini-batch의 cost를 구할 때는 mini-batch loss 값을 구해서 mini-batch 안의 sample의 크기로 나눠준다 ..
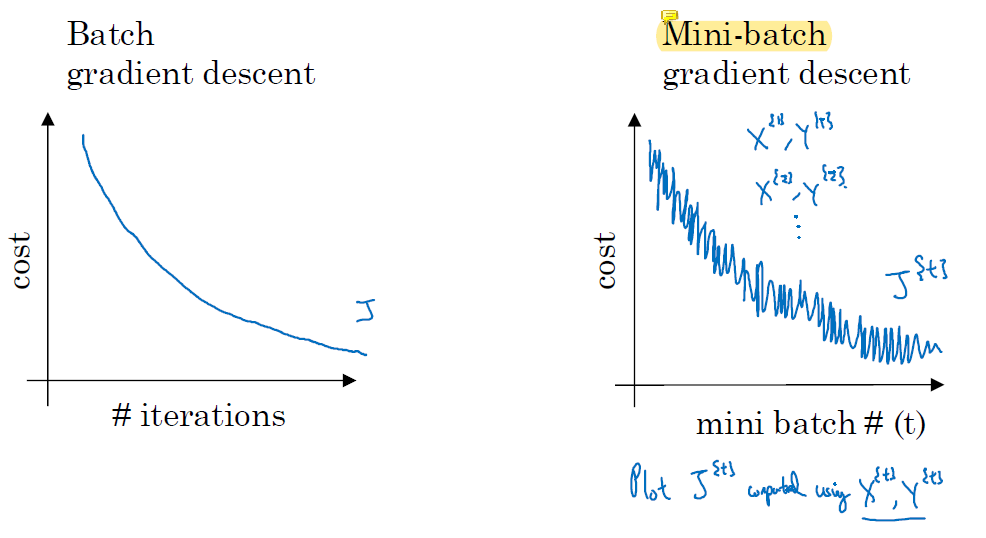batch gradient는 iteration을 반복할수록 cost function이 값이 작아진다.
하지만 mini-batch gradient descent는 training sample에 대한 loss가 성공적으로 감소하긴 하지만 noise가 있다. 전체적으로 봤을 때는 시간이 흐르면 상당히 loss가 감소한다. mini-batch에 따라 training이 쉬운 sample만 들어있을 수도 있고 training이 어려운 sample만 들어있을 수도 있지만 결론적으로는 모든 sample을 다 사용해 training을 하게 되므로 batch의 training 결과와 비슷하거나 더 좋아진다.
batch는 local optima에 빠질 수 있고 한 번 빠지면 탈출할 수 없지만 mini-batch는 운좋게 local optima를 탈출할 수 있다. batch는 gradient가 0에 수렴하면 그 gradient가 유지되지만 mini-batch는 noise로 인해 gradient가 0이 아니므로 local optima를 탈출할 수 있다.

mini-batch size가 m과 동일해지면 batch gradient descent와 동일해진다. 안정적이고 정확하지만 느린 gradient이다. gradient를 구해 update하는데에 시간이 오래 걸린다.
mini-batch size가 1이 되면 vectorization을 못써서 stochastic gradient가 된다. 그래서 noise가 더 커진다. noisy하지만 언젠가는 수렴하는 계산이 매우 빠른 gradient.. gradient 계산 자체는 빠른데 vectorization이 안돼서 전체 update는 느리다.

따라서 mini-batch size는 1~m 사이로 정한다.

또한 m이 작으면 mini-batch를 사용할 필요가 없다. mini-batch는 보통 memory에 training data를 전부 올리지 못하는 경우에 사용한다. 몇백 GB의 데이터.. 그래서 mini-batch의 size는 memory를 꽉 채우는 size로 결정한다.

Batch Normalization

mini-batch에서는 선형변환결과 z와 비선형변환 결화인 a중 z를 정규화한다.

여기서 평균을 구할 때 사용하는 m은 전체 sample의 개수를 의미하는 것이 아닌 mini-batch 내의 sample의 개수임에 주의해야 한다.

γ와 β는 training이 가능한 변수이다. Znorm은 평균이 0, 분산이 1인데 그 값이 optimal이 아닐 수도 있기 때문에 그 값을 정하기 어려워서 γ, β로 feature의 부호나 평균, 분산 같은 것들이 변한다.

γ와 β를 training한 결과가 다음과 같아진다면
normalize할 필요가 없다는 뜻이다. 어차피 결과가 똑같은데 정규화를 할 필요가 없다. 정규화 과정은 오히려 방해가 된다.

output layer는 batch normalization하지 않는다. hidden layer는 언제든 batch normalize가 가능하다.
batch normalization은 output을 구하는 데에 방해가 된다. 결과가 0 또는 1로 나와야 하는데 이를 정규화하면 평균이 0으로 맞춰지기 때문이다.

batch-normalization은 무조건 그 mini-batch에만 해야한다. mini-batch에서 평균과 분산을 구해야 한다는 뜻... mini-batch마다 조금씩 평균과 분산이 다르기 때문에 다른 mini-batch가 들어오면 이 값들이 달라진다.
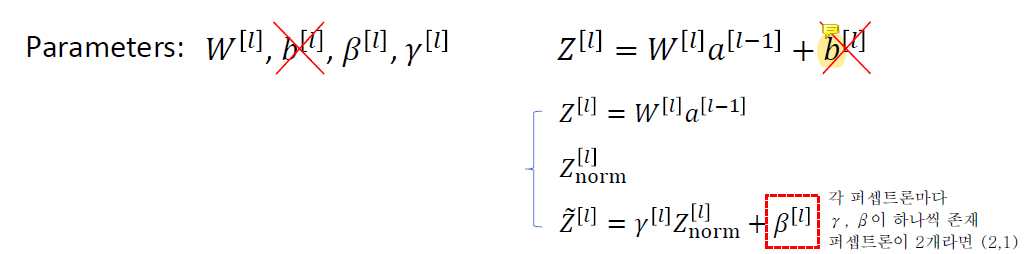
b와 β의 기능이 완전히 동일하기 때문에 b를 생략할 수 있다. b는 있으나 마나 의미가 없다.. 어차피 z를 정규화하면 평균이 0이 되도록 b가 날아가고 shift될 것이기 때문이다.
따라서 b는 learning하지 않는다.

같은 이유로 gradient descent를 계산할 때도 db는 계산하지 않는다.

training에서 batch normalization을 사용했다면 test에서도 무조건 batch normalization을 사용해야 한다. 그런데 보통 test할 때는 sample의 수가 많지 않다.
만약 sample이 하나라면 mini-batch안에 sample이 하나여서 평균, 분산과 같은 것을 구할 수 없다. 그 때에는 training에서 사용했던 값들을 가져와 사용한다. 마지막 mini-batch의 평균과 분산을 가져올 수도 있고 여러 mini-batch의 평균과 분산을 모아서 평균을 사용할 수도 있다.

Covariate Shift

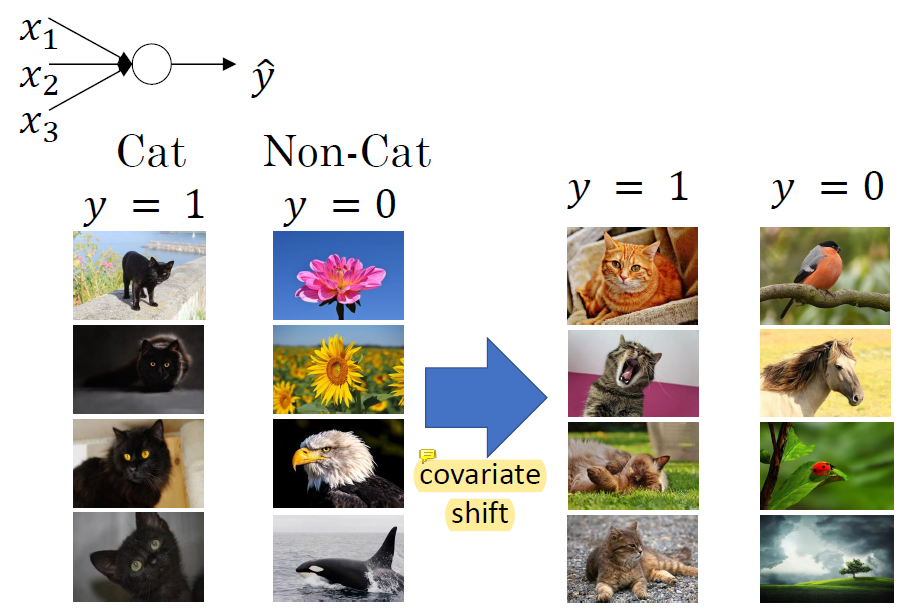covariate shift는 training data와 test data의 misalignment로 인해 발생한다. 고양이 문제를 푸는데 training 할 때는 검정색 고양이만 써서 학습시키고 실제로는 일반 고양이 사진으로 test하면 문제를 제대로 풀 수 없다. distribution이 다르기 때문임. 이 때 covariate shift 문제가 발생했다고 함.
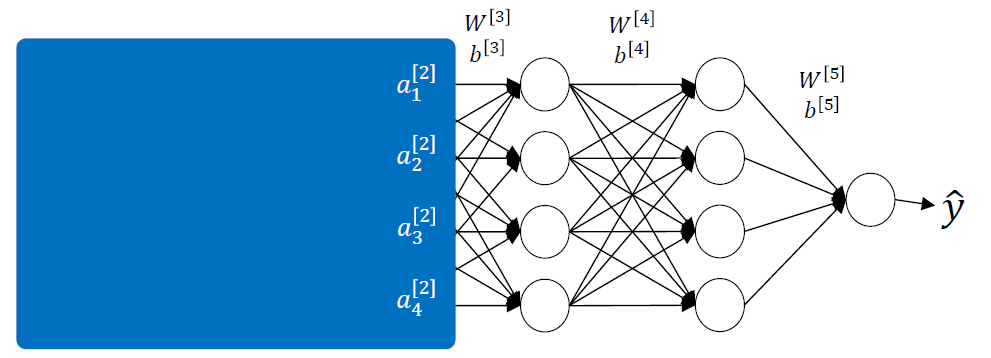전체 neural network를 a1, a2, a3, a4가 input인 3 layer neural network로 생각하면 y hat을 줄이기 위한 방향으로 W와 b를 update할 것이다.
그런데 backpropagation을 사용하면 자신만 update하는 것이 아니라 자신 이전의 W와 b까지 영향을 미쳐 upate하게 되기 때문에 문제가 생긴다. 그럼 3번째 layer입장에서는 그 다음 learning에서는 똑같은 그림이 input으로 들어왔는데도 different input을 받게 되는 것이다. 바뀐 W와 b로 인해 a값이 달라지기 때문.. 이것이 covariate shift를 유발한다.

그런데 각 layer에 batch normalization을 적용하면 항상 data가 normalize되어서 a가 나오니까 똑같은 그림에 대해서 어느정도 비슷한 a값을 얻을 수 있어서 covariate shift문제를 어느정도 피할 수 있다.