Exponentially Weighted Averages

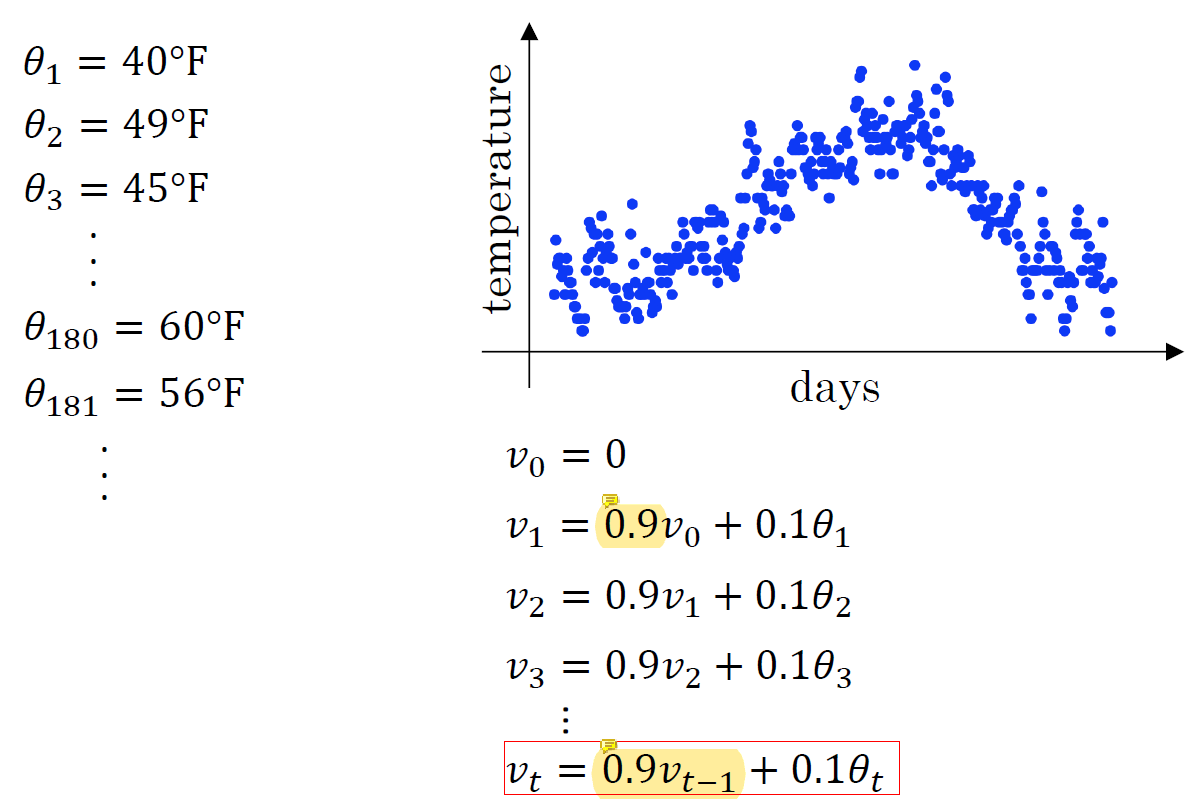temperature의 값을 나타냈을 때 값들에 noise가 섞여있다. noise를 없애는 가장 쉬운 방법은 average를 사용하는 것이다.

식에 곱해진 0.9는 smoothness의 강도를 결정한다. 이전 단계에서 smooth된 data에 smoothness를 적용하는 것을 반복한다.
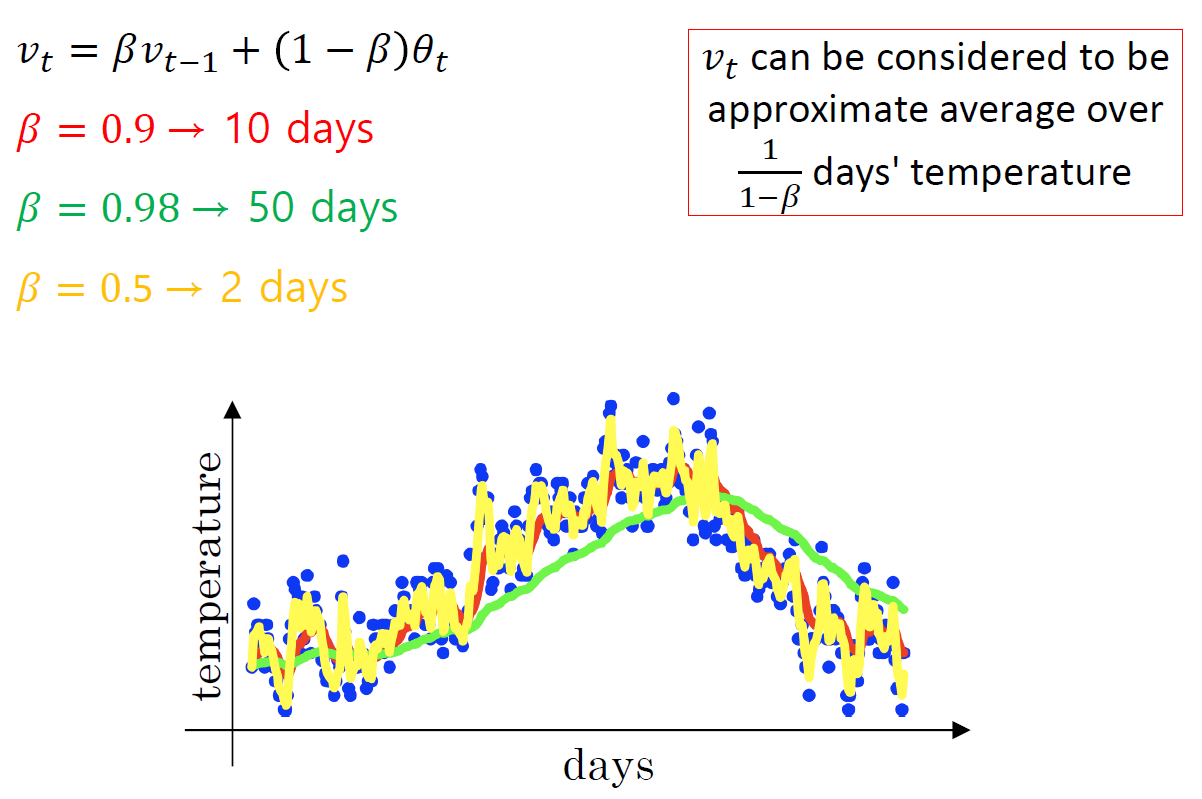
β는 smoothness의 강도를 결정하는 hyperparameter이다.

β = 0.9이면 1/(1-β) = 10day의 average와 결과가 비슷해진다. 현재 sample을 포함해 과거의 9개 sample을 고려해 만든 version이란 뜻이다. 그럼 엄청 smooth해지는 것.

같은 방법으로 β = 0.98이면 50일, β = 0.5면 2일의 average를 취한 것과 비슷해진다. β가 커질수록 더 많은 data의 평균을 취하는 것이 되므로 더욱 data가 smooth해진다.

β를 너무 키워서 너무 smooth해지면 원래 있던 기존의 peak가 뒤로 밀리는 delay가 생길 수 있다. 이런 delay를 감내할 수 있는 범위에서 값을 청해야 한다. 그렇다고 β를 너무 작게 하면 smooth하는 의미가 없어지고..
실제로 β = 0.9가 많은 경우에 default parameter로 쓰이고 있다.
β의 값이 exponential하게 계속 줄어들기 때문에 exponentially weighted라고 한다.

Bias Correction

v1을 구하기 위해 필요한 v0가 없기 때문에 임의로 정의를 해야한다. 하지만 초기값 v0이 0이기 때문에 v1을 구할 때 이 값을 사용해버리면 의도치않게 v1의 값이 0에 가까워지는 문제점이 생긴다. 따라서 v1을 구할 때 v0를 사용하는 term은 지운다.

bias correction vt -> vt/(1-β^t)는 starting point에서 초록색 선과 보라색 선을 일치시키기 위한 방법이다. t가 엄청 커지면 β^t가 0에 수렴하게 되면서 분모가 1에 가까워지고 자연스럽게 bias를 고려하지 않게 된다.

Gradient Descent With Momentum

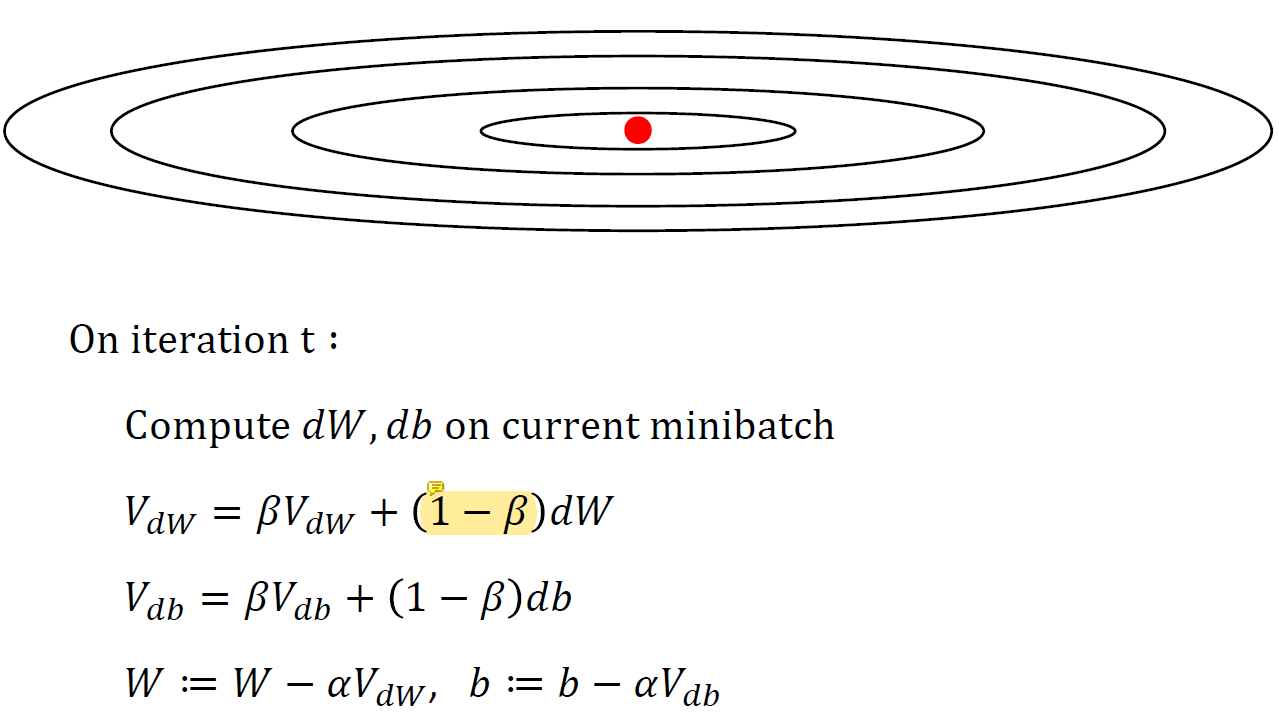mini-batch를 통해 gradient descent를 사용하면 빨간 점에 도달은 하겠지만 굉장히 noisy할 것이다. 그래서 noise가 좀 덜하게 빨간점으로 잘 가게 하기 위해서 1-β로 smooth를 해준다.

이 경우에는 bias가 critical하지 않기 때문에 굳이 bias correction을 하지 않는다.
α, β가 hyperparameter이지만 β = 0.9를 사용할 수 있다.

RMS Prop

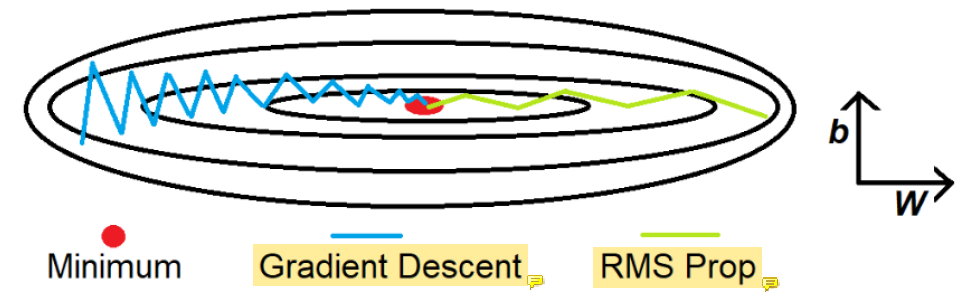그냥 gradient descent를 썼을 때 noise가 심하기 때문에 RMS Prop을 사용한다. RMS prop은 단순히 smooth만 하는 것이 아니라 minimum으로 가는 속도를 조절한다. 세로방향의 gradient는 0이었으면 좋겠고 가로방향의 gradient는 컸으면 좋겠다고 생각한다.
update가 느린 애들은 빠르게 확 보내주고 update가 빠른 애들은 좀 늦춰서 보내주고... RMS prop은 gradient descent보다 거의 무조건 성능이 좋다.
RMS prop은 W를 키우고 b를 줄이고 싶어한다. Sdw가 1보다 작으면 W의 값이 엄청 커지고 Sdb이 1보다 크면 b가 엄청 작아지므로 작은 Sdw와 큰 Sdb가 필요하다.

Adam

Adam은 진화한 gradient descent이다. v는 그냥 gradient를 사용하고 S는 dW^2를 사용한다.
W와 b를 구할 때는 gradient가 비슷한 값을 유지할 수 있도록 분모로 나눠준다.
Adam은 bias correction을 사용하긴 하지만 큰 영향을 미치지는 않는다. training을 엄청 오래 해서 작은 error나 bias는 없어지기 때문이다.
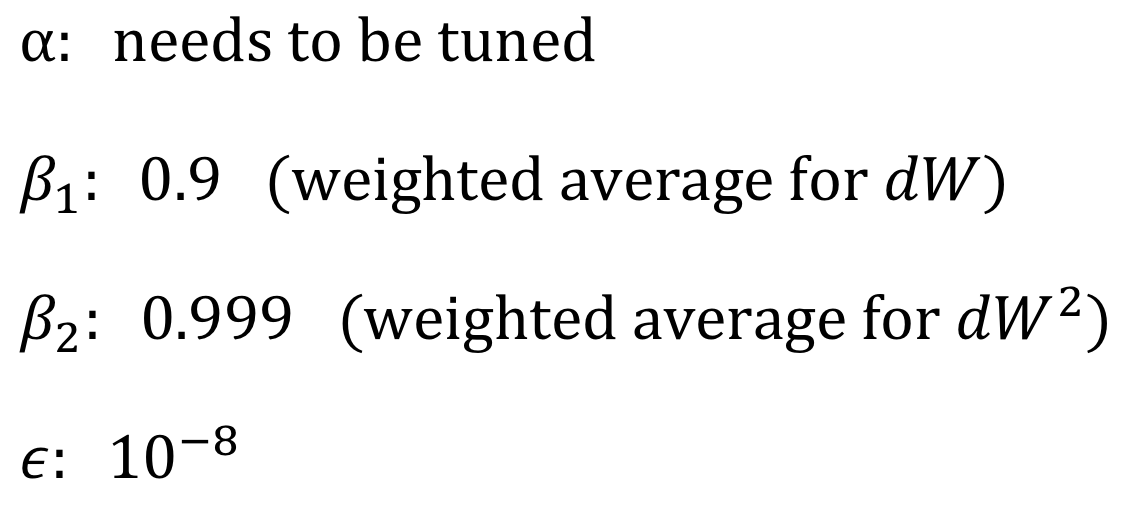Adam에서 hyperparameter값은 앵간한 상황에서 default를 사용한다. 굳이 learning할 필요가 없다는 뜻!
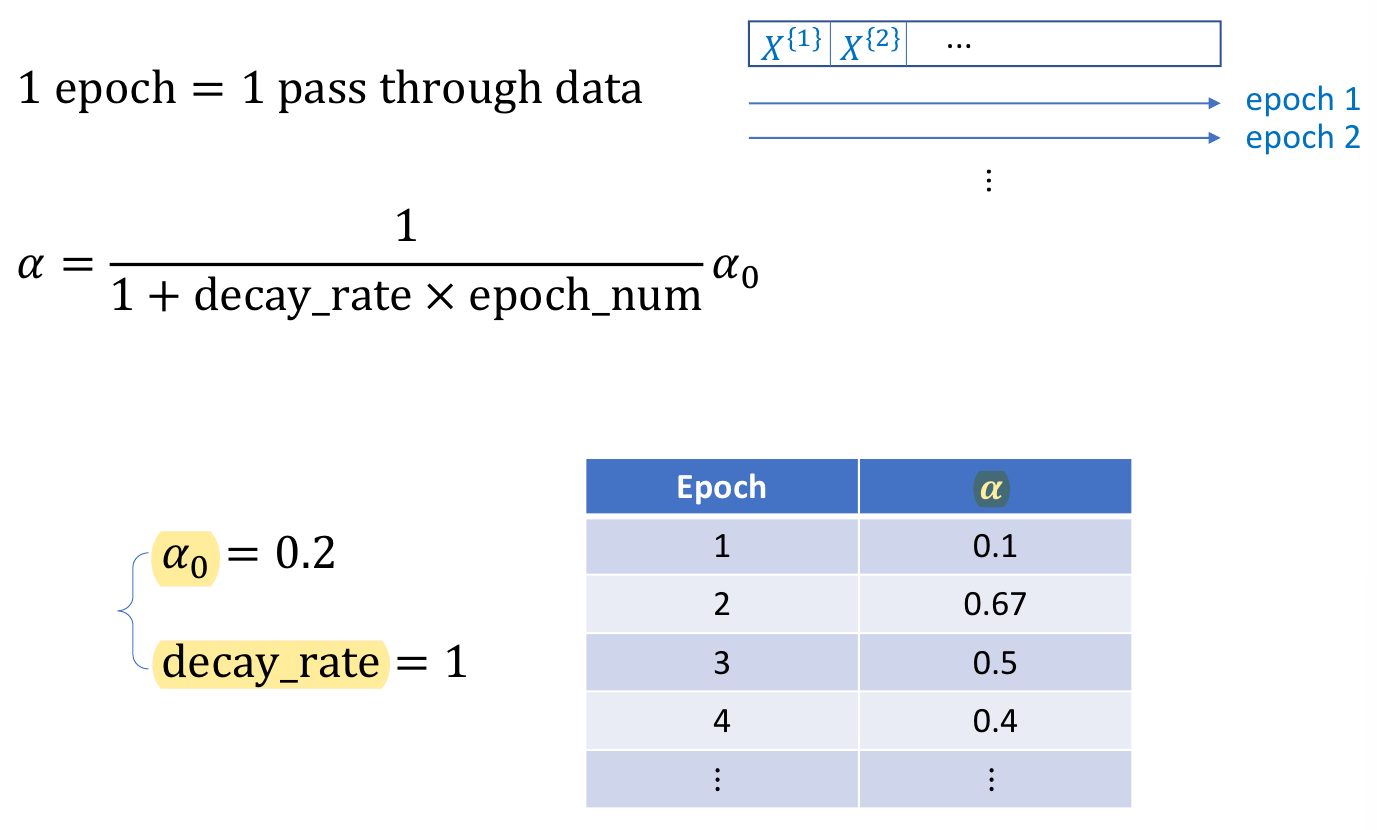
α와 decay_rate는 hyperparameter이다. iteration이 많아질수록 learning rate α값은 작아지고 learning 초반에 빠르게 감소하는 경향이 있다.
α값을 epoch에 따라 임의로 조절하기도 한다.

Local Optima In Neural Networks

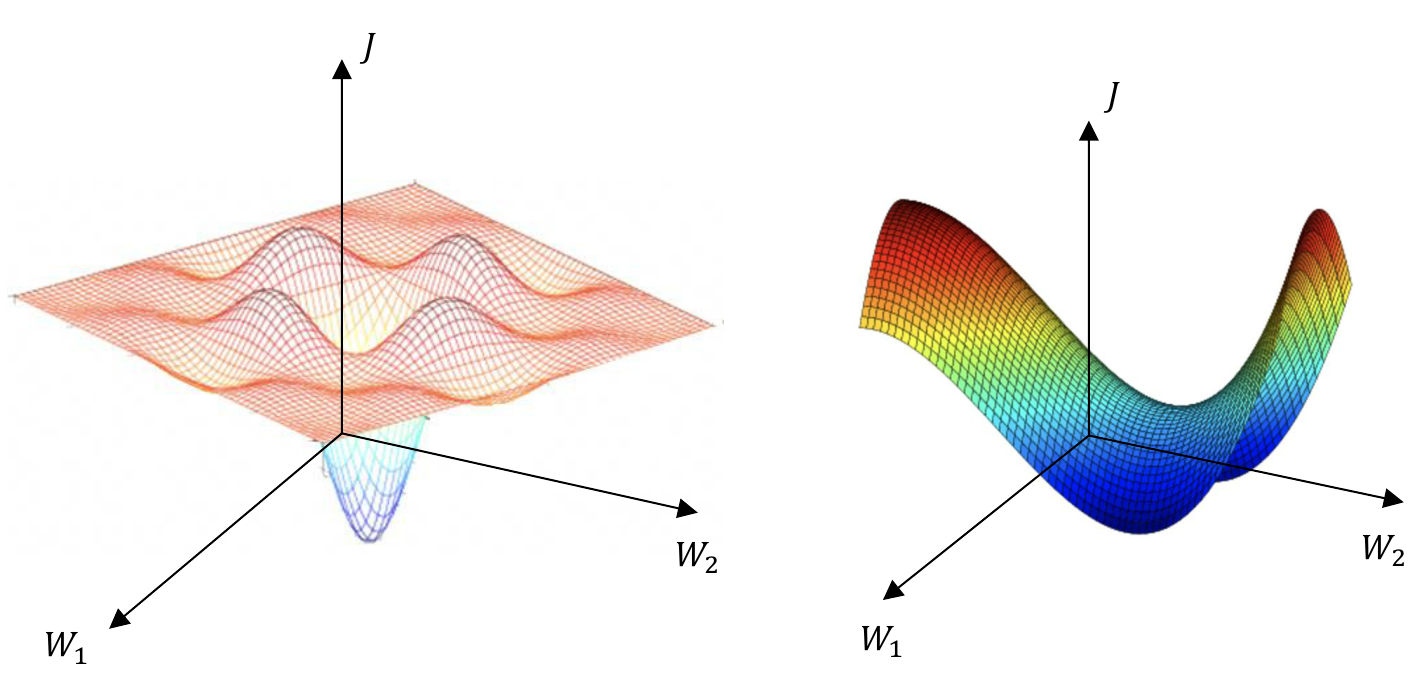예전에는 solution space가 왼쪽처럼 엄청 복잡할거라고 생각했다. 엄청 많은 local optima가 있을 것이라고 생각했지만 실제로는 solution space가 오른쪽처럼 그닥 복잡하지 않았다. 말 안장처럼 평평하게 생긴... 대부분의 w(gradient)가 평평한 곳에 있고 나머지만 큰 값을 가지는.
전체 중 99개는 거의 learning하지 못하고 멈추는 것임. update가 되는 위치를 잘 따라가면 느리지만 solution을 얻을 수는 있음. 하지만 update가 굉장히 오래걸림. 대부분의 확률로 gradient가 조금밖에 update되지 않기 때문.