training을 하기 위해서 결정해야 할 것들이 정말 많지만 각 hyperparameter 사이에 dependency가 있기 때문에 guess가 매우 어렵다. 그렇기 때문에 실제로 machine learning은 굉장히 반복적인 작업이다.

Dataset

좋은 choice를 위해 training sets, development sets, test sets를 이용할 수 있다.
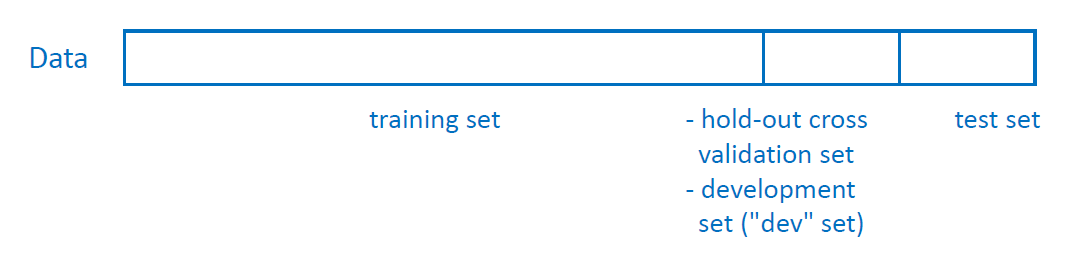development set을 validation set이라고 부르기도 한다.

어떤 dataset이 주어졌을 때, 전체 sample에서 70%를 training set, 30%를 test set으로 나누거나 60%를 training set, 20%를 development set, 20%를 test set으로 나누는 것이 일종의 convention처럼 사용된다. 이 세 set 사이에는 overlap이 없어야 한다. 즉 각 set이 독립적이어야 하고 중복되는 sample이 없어야 한다.

만약 data의 수가 매우 많다면 training data를 99%, development set을 1%로 사용하기도 한다. development set은 검증용이기 때문에 그렇게까지 많을 필요는 없는데 data의 수가 워낙 많으면 1%만 사용해도 sample이 엄청 많으니까 test용으로 충분하다는 의미이다.

K-Fold Cross-Validation

training sample의 양이 적을 때 사용하는 방법이다. training sample의 양이 적으면 운이 좋아서 learning이 엄청 잘 되거나(이런 경우는 거의 없음) 운이 나빠서 learning이 엄청 안되거나 할 수 있는데 이런 극단적인 케이스를 피하기 위해서 여러 번 반복해서 test를 하는 것이다.

1. 전체 dataset을 K fold로 나눈다. typically K는 5 혹은 10이다.
2. 첫번째 fold가 test set으로 간주되고 나머지 K-1 fold로 network를 training한다. K등분한 것 중 하나를 test set으로 사용하고 나머지는 training set으로 사용한다는 의미이다.
3. 위의 과정을 K번 반복한다. dataset의 각각 다른 fold를 test set으로 선택하는 것 같음... 매 iteration마다 새롭게 dataset을 나누기도 하는 것 같다.
4. K test error를 averaging해서 estimated test error를 구한다.

data를 splitting할 때 training set, test set, development set이 같은 분포를 가져야 한다. 고양이 사진 가져다가 training 해놓고 dev랑 test는 강아지 사진 가져다가 쓰면 안된다 이런거임..! 그게 제대로 learning이 될 리가 없긴 해 ㅋㅋ

test set이 없어도 괜찮다! development set만 있어도 상관없다.

Bias and Variance

machine learning에서 bias와 variance의 trade-off은 아주 중요한 문제이다. 하지만 deep learning은 dataset의 크기가 매우 크기 때문에 이런 문제가 많이 줄어들었다.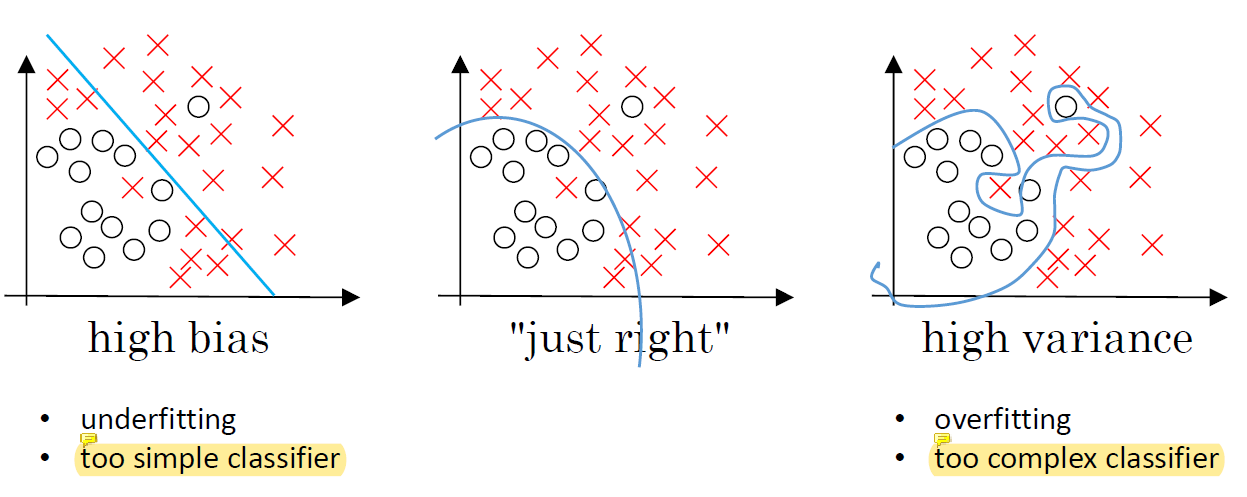

• High bias : underfitting이다. 변수가 너무 적고 단순한 모델을 사용해서 제대로 learning되지 않은 것이다. 주어진 문제를 제대로 풀지 못하는 것.
• High variance : overfitting이다. 너무 복잡한 모델을 사용해서 변수가 많으니까 문제를 외워버리는 것임... 학습시킨 그 문제는 잘 푸는데 새로운 문제를 못풀게 됨. training set은 정확하게 풀지만 그것밖에 못푸는. 보통은 overfitting이 underfitting보다 쓸데가 없다. 몸집만 커서.
  dataset이 작을 때 주로 이런 문제가 발생하는데 dataset이 크다면 이런 문제가 어느정도 해소된다. overfitting은 dataset을 neural network가 외우면서 발생하는건데 data가 매우 많으면 문제를 외우는 것이 거의 불가능하기 때문이다.
• High variance : train 문제는 잘 푸는데 dev set과 error의 gap이 너무 큼.. train 문제만 잘 풀고 test 문제는 풀지 못한다는 뜻이므로 high variance이다.
• High bias : train error가 꽤 크다는건 train 문제를 제대로 풀지 못한다는 뜻임. 시스템이 너무 simple하기 때문임... 전반적으로 문제를 풀지 못하는, 학습도 못하고 실제로 문제도 풀지 못하는 상태이다.
• High bias & High variance : 최악의 경우이다. 두 error 사이의 gap도 크고 error 자체도 커서 train set도 못다루고 test set은 더욱 못 다룬다.
• Low bias & Low variance : 이것이 ideal version임.

위의 설명은 human의 classification error가 0%에 가깝다는 전제가 깔려있기 때문에 가능한 것이다. 만약 인간의 오차가 15% 정도라면 위의 경우에서 15%로 high bias problem이 있다고 할 수 없다.
문제를 풀고 못풀고는 굉장히 주관적인 영역이라 비교대상이 주로 사람이다. 문제를 잘 푸는 사람이 15%정도의 오차를 가진다면 이 경우 neural network가 문제를 못푼다고 말할 수 없다는 얘기.
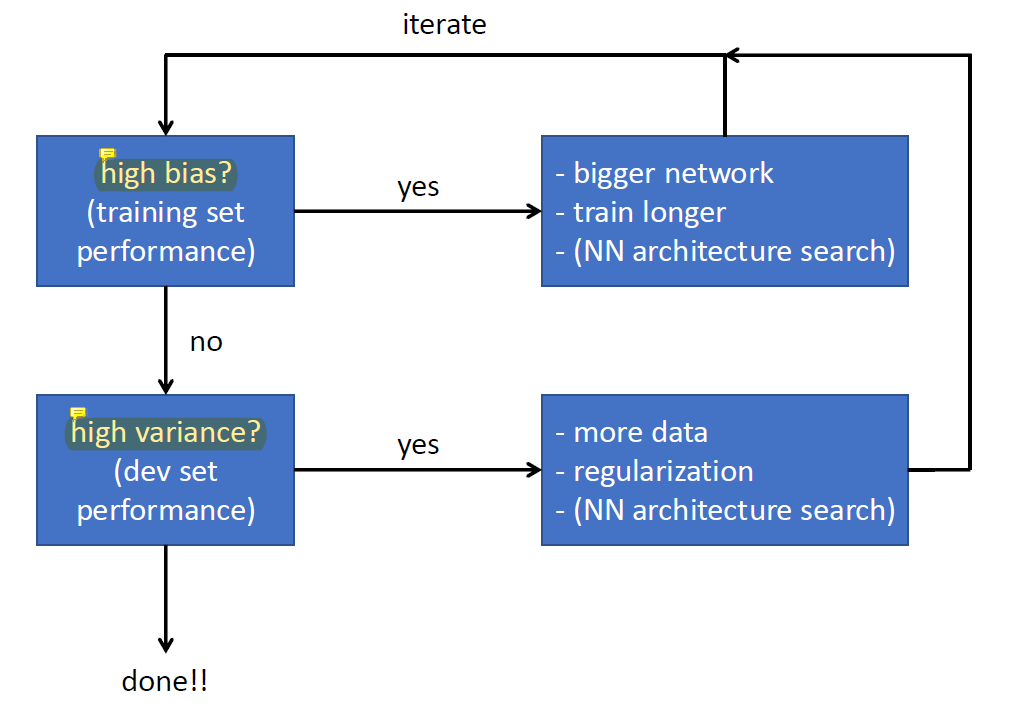neural network가 high bias하다면 network가 너무 simple한 것이므로 parameter를 늘려 bigger network로 만들어야 한다. 이 과정을 반복하면 overfitting의 가능성이 높아지면서 variance가 높아진다.
variance가 높아져서 high variance의 상태가 되면 이 때에는 dataset을 늘린다. dataset을 늘리는 방식은 simple하고 효과가 좋지만 dataset을 구하는 데에 시간과 돈이 많이 든다는 단점이 있다.
하지만 최근의 딥러닝에서는 이미 매우 큰 dataset이 있기 때문에 bias 문제는 낮고 overfitting 문제는 발생하지 않는다.

Regularization

regularization은 overfitting을 방지하고 variance를 줄인다.

logistic regression에서의 regularization을 살펴보자.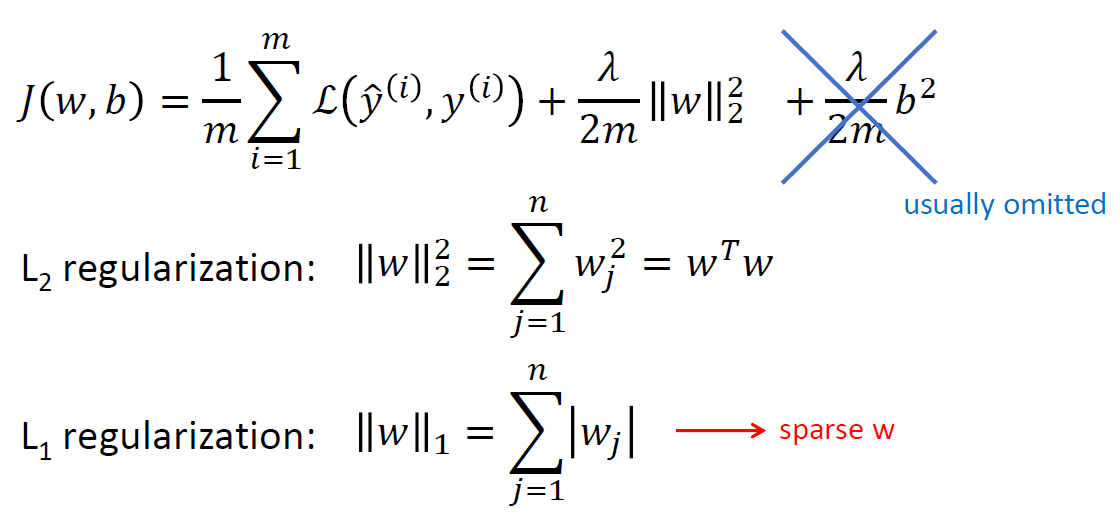L2 regularization은 high variance 문제를 풀기 위해 term을 2개 끼워넣었다고 생각하면 된다. 이 끼워넣은 term들을 regularization term이라고 한다.
끼워넣은 두 term 중 w>>b이기 때문에 b^2의 term은 무시할 수 있다.

남은 term을 생각해보면, 전체 cost를 줄이기 위해 w가 작을 수록 cost가 작아지는데 w가 너무 작아지면 첫번째 항이 이상해져서 값이 매우 커지게 된다. w=0이면 문제를 풀 수 있을 리가 없는 것처럼... 그래서 적당한 w를 찾는게 중요하다.
w가 0에 가까우면 좋겠는데, 원래 문제도 잘 푸는 0에 가까운 w를 찾고자 하는 것임!

여기서 λ는 regularization parameter로, λ=0이면 regularization이 안되고 λ가 매우 크면 regularization을 매우 세게 적용하는 것이다. λ는 실험적으로 정해야하는 hyperparameter 중 하나이다.

L1 regularization은 euclidean distance로 사용하는데 선호도의 차이가 [0,0] > [0.5,0.5] > [0,1]이다 (2차함수의 최솟값이 생기는 지점이 0.5이기 때문. [0,0]을 제일 좋아하지만 [0.5,0.5] > [0,1]사이에는 선호도의 차이가 없다. 문제를 잘 풀기만 한다면 똑같다고 취급함... [1,1]이런 것만 아니면 됨..! 몇 개의 큰 값은 허용할 수 있다. 전체적으로 0을 좋아하지만 몇 개는 커져도 된다 이런 느낌.
기존의 gradient descent에서는 (1-αλ/m)이 없이 backpropagation의 결과가 dW[l]이 되었다.
하지만 regularization을 하면서 (1-αλ/m)이 추가되었고, 이항하였을 때 (1-αλ/m)의 크기가 1보다 작아서 전체적으로 W값을 많이 낮춰주기 때문에 weight를 낮춘다는 뜻으로 weight decay라고 부른다.
λ이 0이면 high variance(overfitting, 시스템이 너무 복잡함), λ이 너무 크면 high bias... 문제를 풀 수 없음.
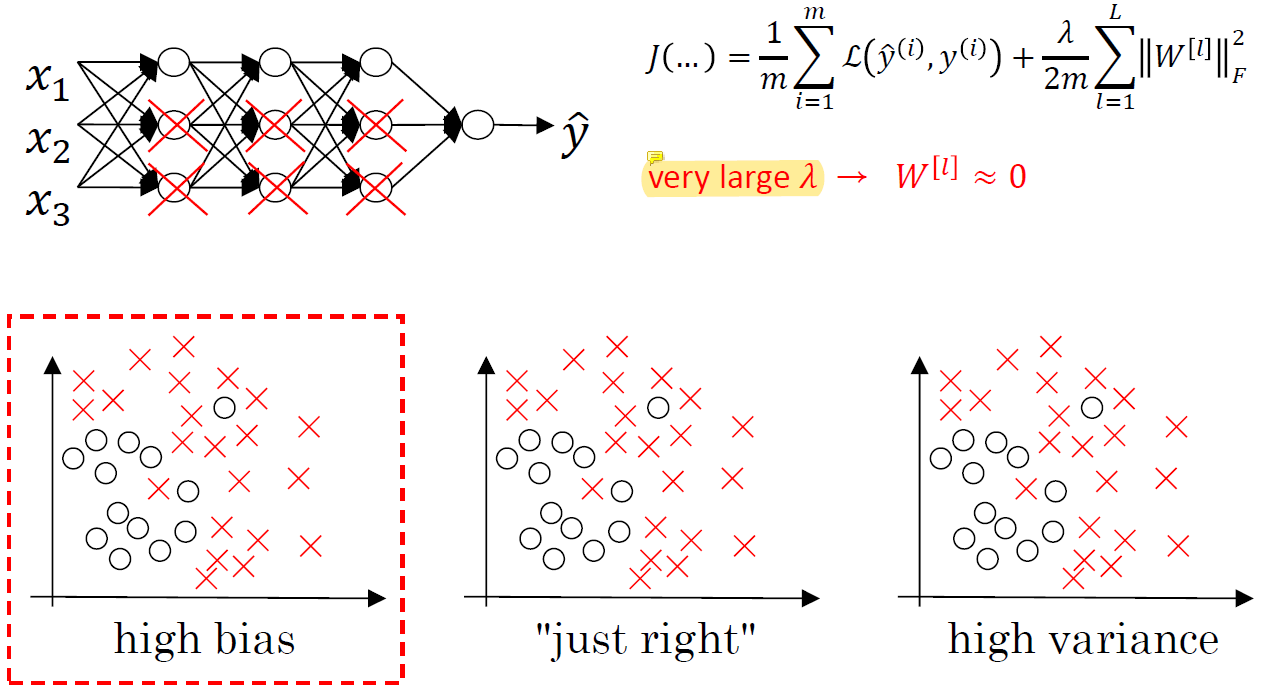맨 처음에 neural network가 overfitting 되었다고 가정했을 때, λ를 매우 큰 값을 취하면 W가 0에 가까워지면서 W를 지울 수 있게 된다. 그럼 복잡한 네트워크를 줄일 수 있게 됨.. 네트워크의 모양을 처음부터 정하기는 힘들지만 이 방법을 사용하면 필요없는 W를 선택적으로 지울 수 있게 된다.
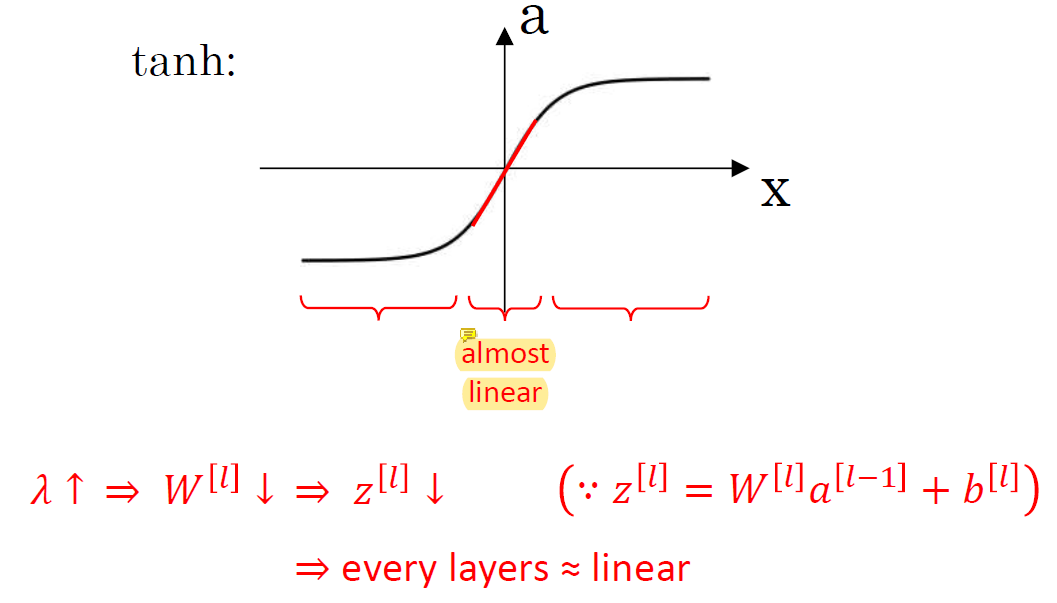input이 0에 가까우면 그래프가 직선에 가까워지기 때문에 non-linearity를 줄 수가 없음.. almost linear라 시스템이 simple해진다. λ가 커지면 W가 거의 0이 되니까 z도 거의 0이 되고 그래서 tanh의 input도 거의 0이 되면서 non-linearity를 줄 수가 없어서 많은 layer의 의미가 없어짐.

Dropout Regularization

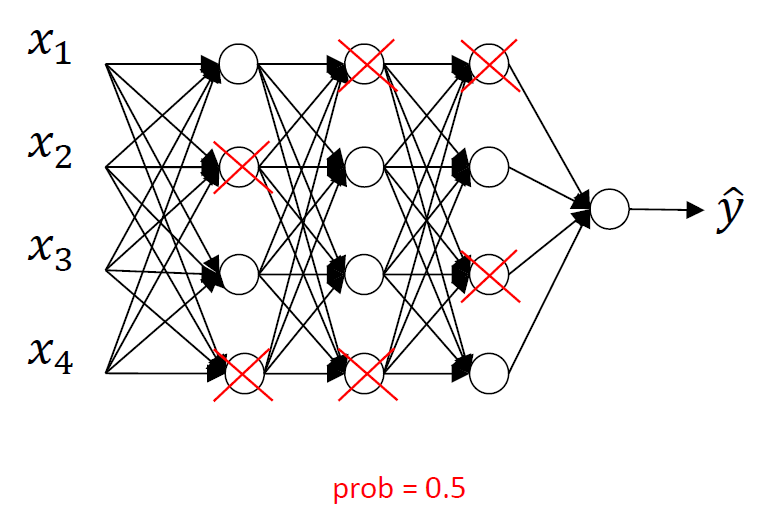일정 확률로 랜덤하게 hidden unit을 지워서 남은 unit의 parameter를 update하는 과정을 반복하는 것임. 각 unit을 확률에 따라 선택해서 삭제하는 것.. 이 확률은 바뀔 수 있음!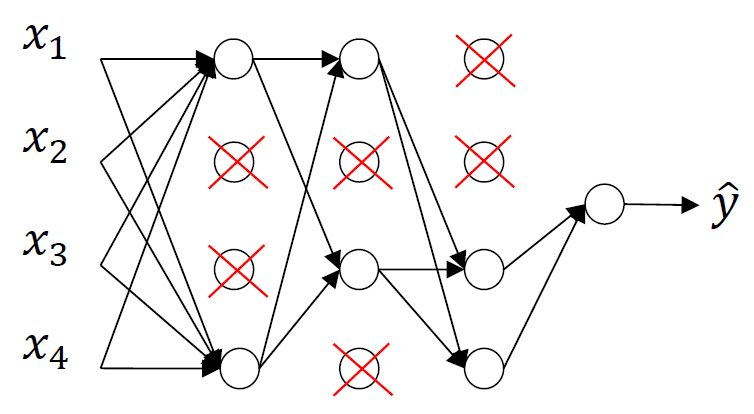/=keep_prob은 scale을 위한 code이다. activation을 scaling한다. 50개의 hidden unit이 있고 그 중 10개가 dropout돼서 remove됐다면 activation 결과도 20%가 줄어듦. 그래서 /=0.8로 그 비율을 fix해주는 것. w와 a를 곱해서 나올거라고 기대했던 값이 조금 줄어든다는거임.. 10개가 없어졌으니까. 50개를 다 써서 결과를 냈으면 100이 나왔을텐데 10개를 안써서 값이 80밖에 안나왔으니까 단순 scaling으로 보상해주는 것.

training을 이렇게 해주면 test때는 dropout을 사용하지 않고 50개의 hidden unit을 제거할 필요 없이 전부 사용할 수 있다.
dropout은 오버피팅되지 않도록 training하고 싶어서 사용하는 것이다. test할때는 전체 네트워크를 굳이 줄이지 않고 다 사용하면 좋지만 trianing할 때 오버피팅되는 것을 피하기 위해 이런 방법을 사용한다.

dropout은 모든 unit이 랜덤하게 지워질 수 있기 때문에 W의 값이 작아진다. 값이 분산되는 것! 각 unit이 언제 지워질지 모르니까 특정 unit이 중요한 일을 맡으면 안된다는거임.. 그래서 특정 unit이 없어지면 안될 정도로 아주 중요한 일을 맡지 못하게 되면서 적당히 조그만 일을 하게 된다. 그래서 한 곳에 값이 집중되지 않고 여러 곳에 분산시켜서 문제를 풀 수 있게 되고 특정 unit의 w값이 엄청나게 커지거자 작아지는 것을 방지한다. w값이 엄청 커지거나 작아진다는 건 그 unit이 중요한 일을 한다는거니까.. 내가 언제든 제거될 수 있으니까 중요한 일은 혼자 하지 말고 나눠서 풀어야겠다! 고 하는 것.

output layer은 dropout으로 remove하지 않는다. 그래서 keep_prob이 1.0임. dropout은 hidden layer에만 적용됨.
또한 layer마다 다른 probability를 사용할 수 있다.

Data Augmentation

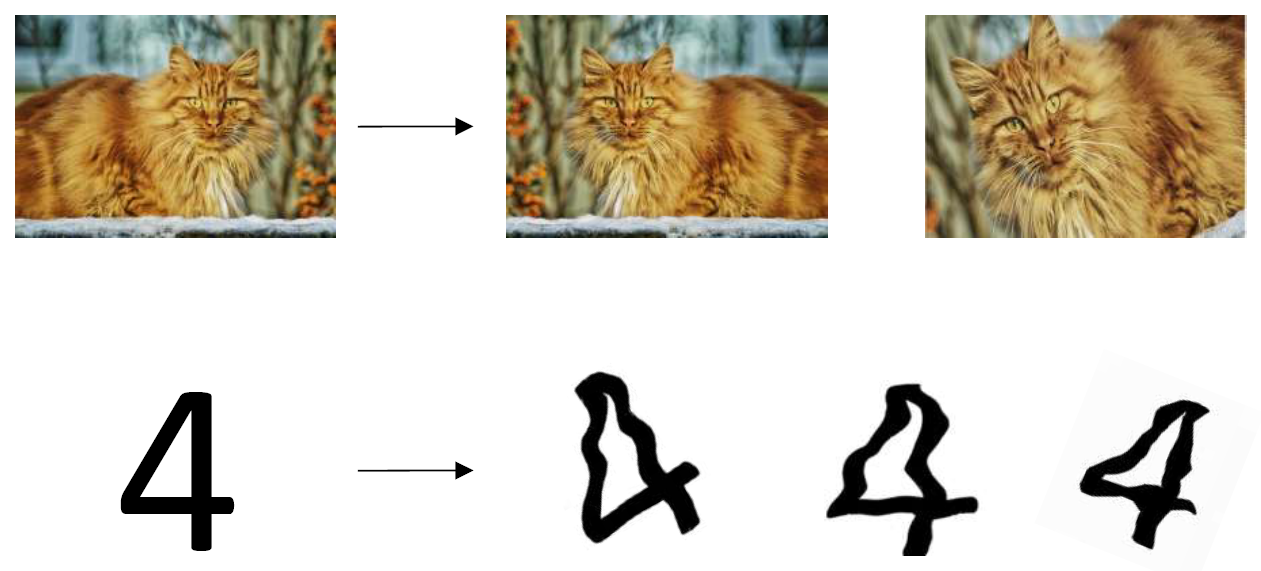large number of data set을 만드는게 시간이 오래 걸리기 때문에 augmentation을 이용해서 data set의 크기를 늘린다. image를 transform해서 쉽게 data set의 크기를 늘리는 것임....
사실 새로운 data를 찾는게 best지만 이 방법은 쉽게 성능을 끌어올릴 수 있도록 도와준다. 거의 무조건 쓴다고 보면 됨! 필수적인 테크닉...
augentation을 너무 심하게 해서 6을 9로 만드는 그런건 안된다. data의 의미가 바뀌지 않는 선에서 transform!

Early Stopping

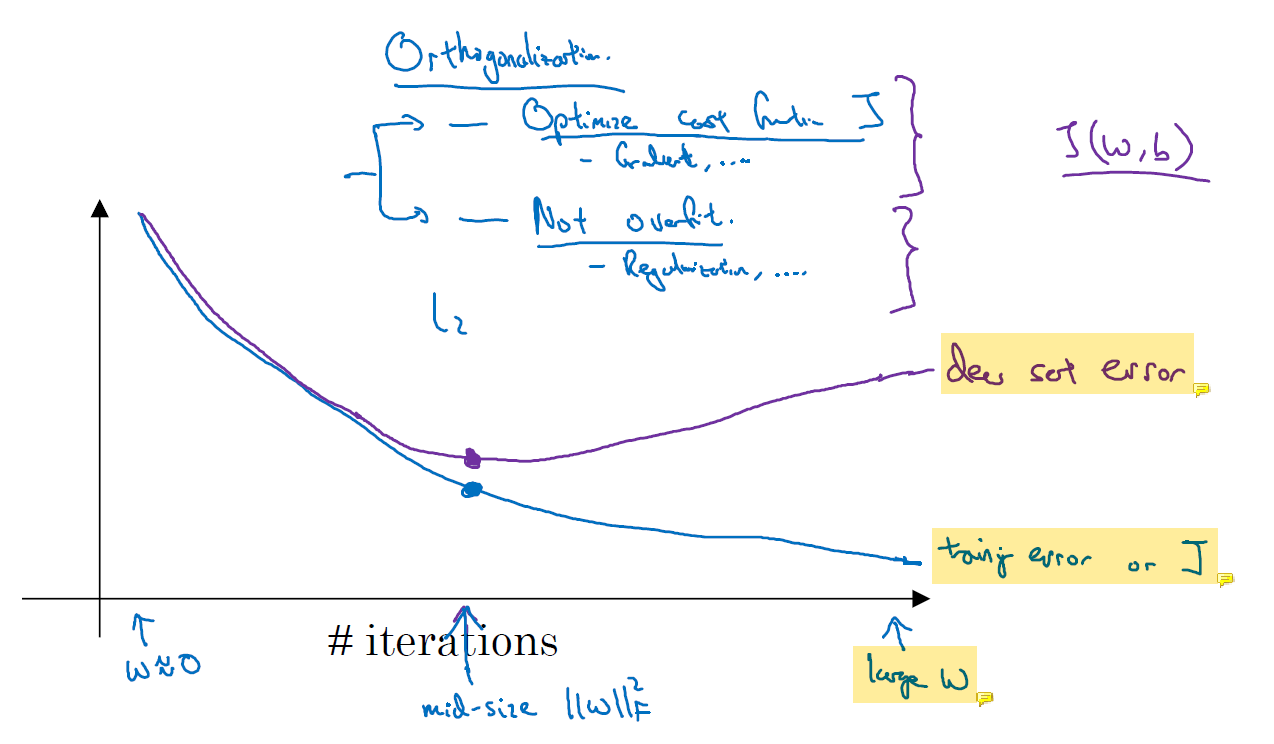training을 할 때는 loss function의 값이 무조건 감소한다. 그것이 training의 목표이기 때문이다.
test set error는 training error와 달리 줄어들기만 하지 않는다. dev set error는 줄어들기만 하지 않고 어느 순간부터 늘어날 수도 있다. iteration이 반복되면서 model이 overfitting되기 시작하고 w가 커진다. training을 오래 하면서 학습 data를 network가 외우는 것이다. 그러면서 특정 parameter의 값이 엄청 커질 수 있다. 항상 그런건 아니지만.. 그럼 training error와 dev set error 사이의 gap이 벌어지게 된다. 이것이 바로 high variance problem이다.

그래서 문제를 잘 푸는 적당한 지점에서 training을 멈춰야 한다. 이는 data set이 별로 없을 때 쓰는 방법이다. 네트워크를 적은 data로 너무 오래 training하면 overfitting될 수 있기 때문이다.

Normalizing Training Sets

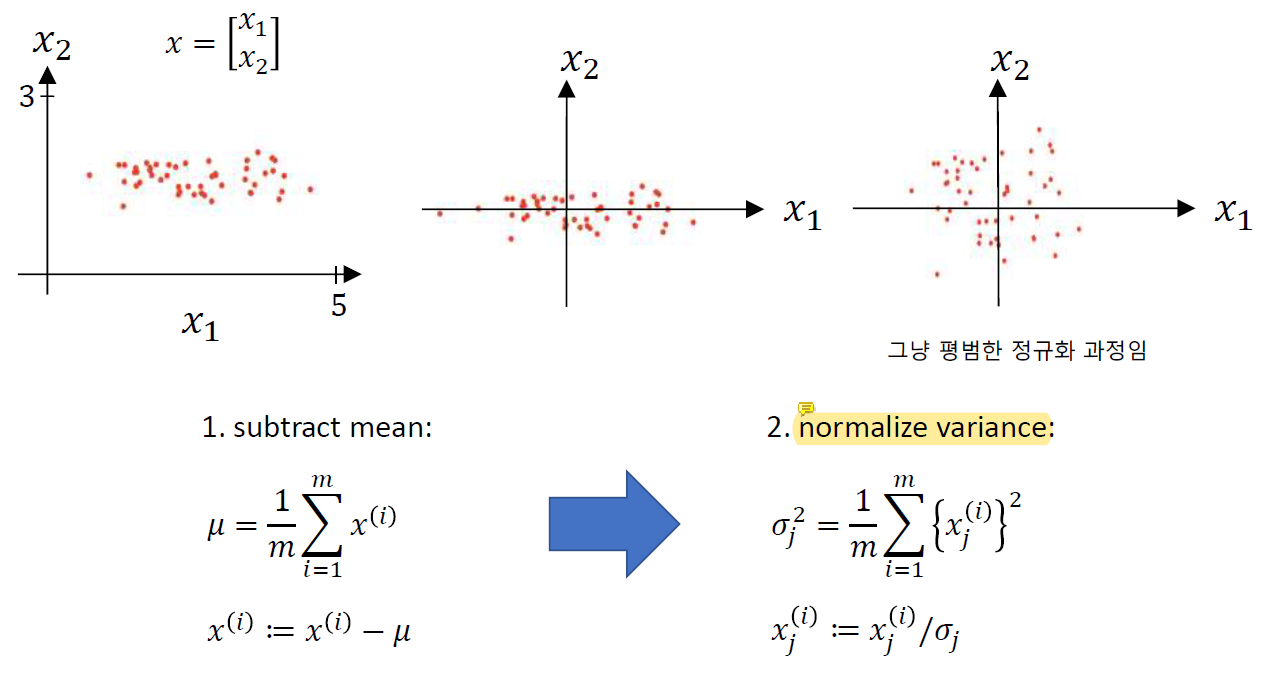normalizing은 그냥 평범한 정규화 과정이다. 평균 뺀걸 표준편차로 나눠주는...
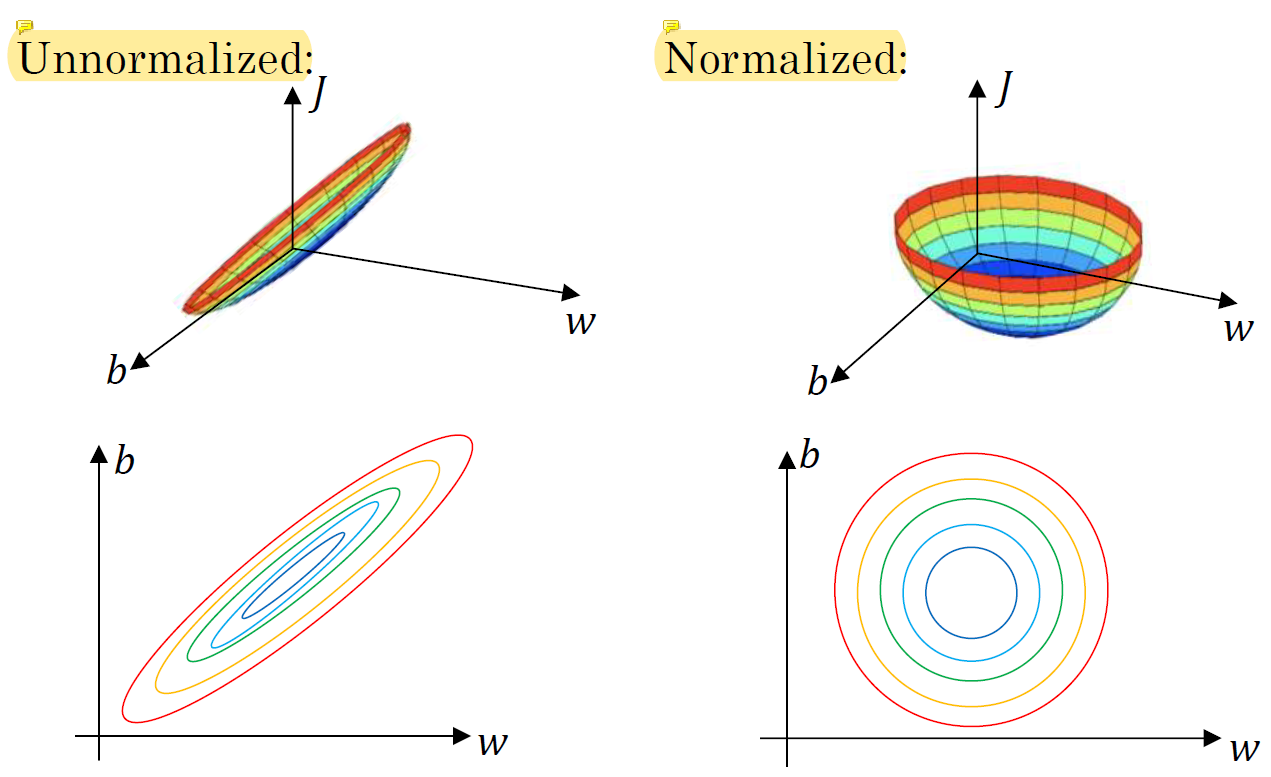normalize를 하지 않으면 data가 편향적으로 존재하기 때문이 운이 나쁘면 loss가 제일 작은 곳(중심부)을 가는 시간이 오래걸릴 수 있다. 각 지점에 따라 중심까지의 거리가 다르기 때문이다.

하지만 normalize를 수행하면 loss function이 well-shaped라 어느 지점에서 시작하든 쉽게 loss가 가장 작은 지점에 쉽게 도착할 수 있다.

normalize를 하지 않으면 큰 x1과 작은 x2가 존재할 때 w1은 조금만 커져도 x1에 의해 그 차이가 매우 커지고 w2는 x2로 인해 값이 크게 바뀌어야 전체 결과에 영향을 미칠 수 있게 된다. 이런 편향적인 문제를 피하기 위해 정규화를 수행한다.

Vanishing / Exploding Gradients

vanishing/exploding gradient는 깊은 네트워크일 때 발생하는 문제이다. 네트워크가 깊어짐에 따라 w를 1 언저리로 유지하기가 힘들어서 발생한다.

• Vanishing gradient : w가 0에 가까우면 gradient를 거의 update할 수 없거나 output이 지나치게 작은 값이 될 수 있다.
• Exploding gradient : w가 크면 output이 너무 커질 수 있다. update는 많이 되지만 너무 과하게 update를 해서 이상한 지점으로 갈 수도 있다.
  backpropagation은 뒤에서부터 계산하기 때문에 뒤쪽에서는 문제가 잘 발생하지 않다가 update하면서 앞쪽에 도달하면 W값이 중첩되면서 vanishing/exploding gradient 문제가 생길 수 있다.
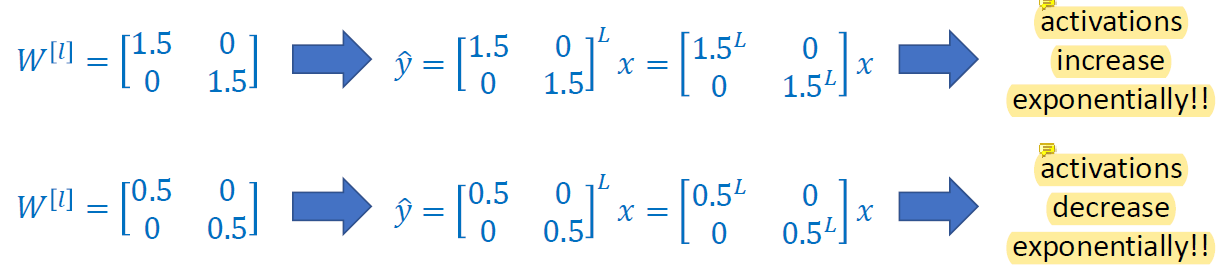
  W가 1보다 크면 exponent될 때마다 값이 엄청 커지고 1보다 작으면 exponent 될 때마다 값이 너무 작아짐.

Weight Initialization for Deep Network

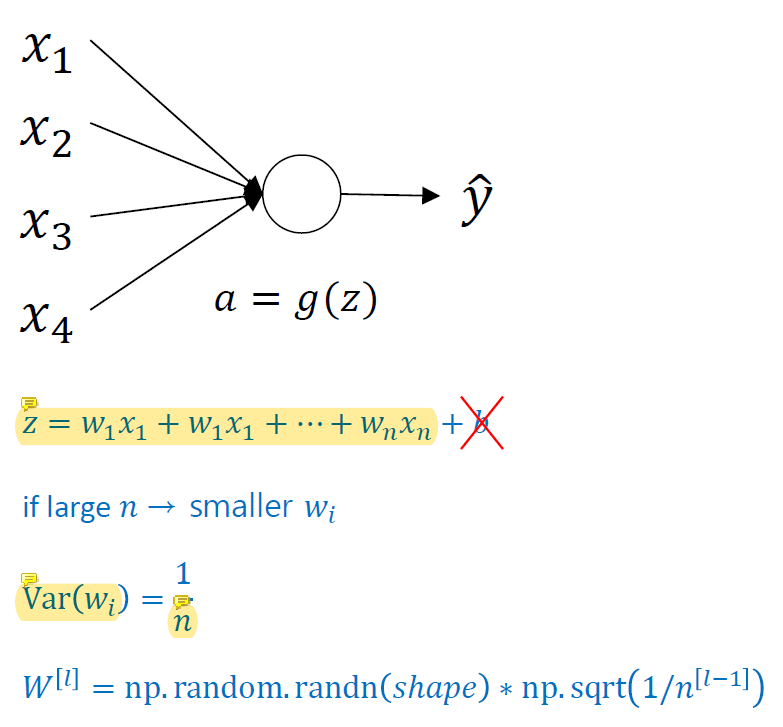
w를 initialize할 때 input이 엄청 많으면 weighted sum z가 엄청 커질 수 있고 input이 엄청 적으면 z가 작아질 수도 있어서 input 개수에 따라w 초기값을 다르게 세팅한다.

보통 Var(wi)의 optiaml이 뭔지 우리는 알 수 없기 때문에 이 값도 변수로 두고 training하는 경우가 많다. 이 값을 1/n으로 정하는 것은 input의 개수를 고려하기 때문이다.