
Image Filtering
output image와 input image는 같은 크기이다 (image 크기가 변하지는 않음).
image filtering에는 linear filtering과 non-linear filtering이 있다.
Linear filtering
linear filtering은 단순히 입력 data를 주변 pixel을 이용해 적당히 weighted sum 하는 것이다. convolution은 linear filtering 중 하나이다.
그리고 learning하는 과정에서 linear transformation과 non-linear transformation을 각각 한 번씩 수행하는데 이 때 linear transformation으로 convolution을 사용하는 것이 CNN이다.
Point Spread Function (PSF)
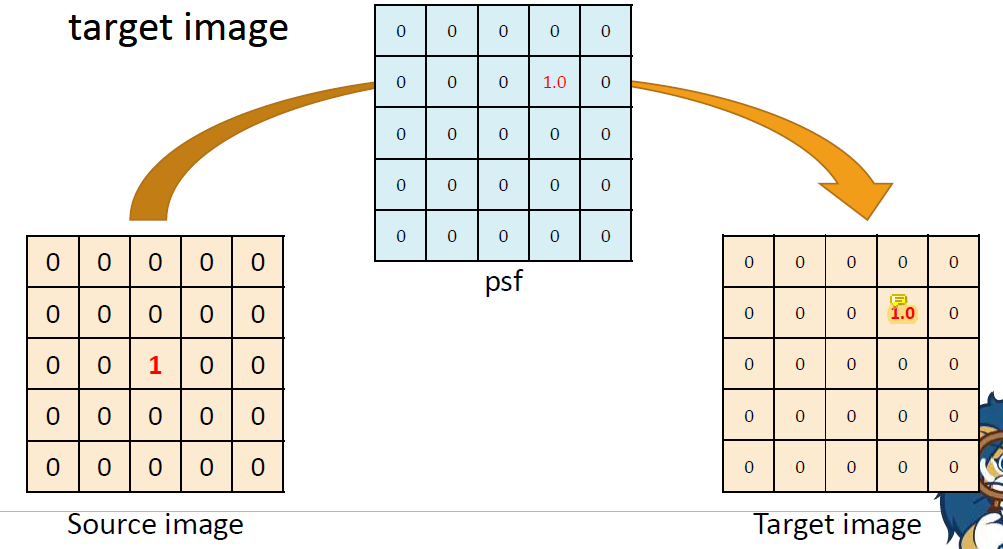
PSF는 image filtering을 하기 위한 linear function이다. source image의 점이 target image로 어떻게 옮겨가는지 나타내줌 ..
점을 이동시키는 위치와 크기를 나타낸다고 보면 쉽다.
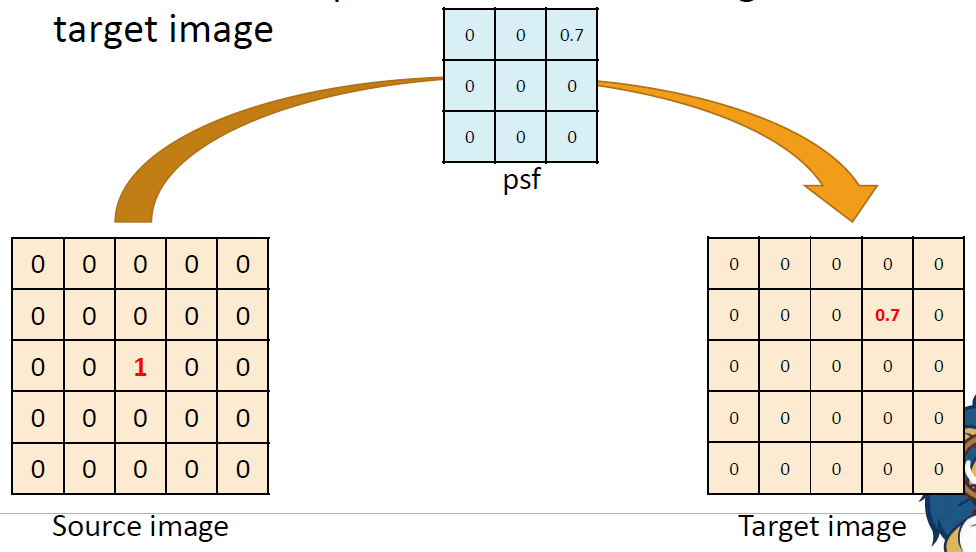
만약 psf에 있는 값이 0.7이었다면 target image에서 1.0의 값은 0.7이 되었을 것이다. (source image value) * 0.7을 수행했기 때문이다.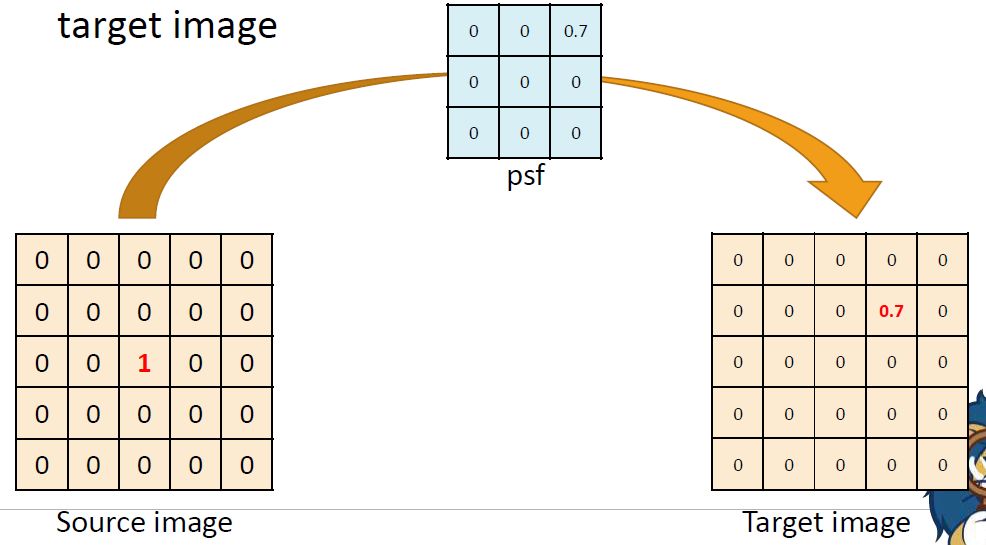
psf의 크기가 source image에 비해 작더라도 같은 방법으로 적용하면 된다. psf의 오른쪽 위에 0.7이 있기 때문에 target image에서는 source image의 1이 0.7로 바뀌면서 오른쪽 위로 이동하였다.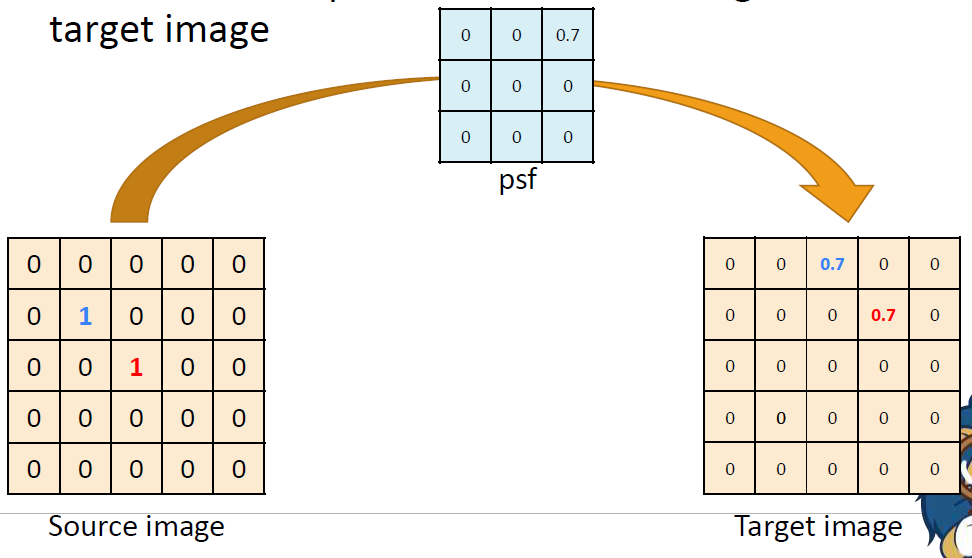 source image에 값이
source image에 값이 0이 아닌 pixel이 여러 개 있을 때 psf는 각각의 pixel에 대해서 독립적으로 적용된다. 두 1 모두 psf에 의해 0.7로 바뀌면서 오른쪽 위로 이동한다.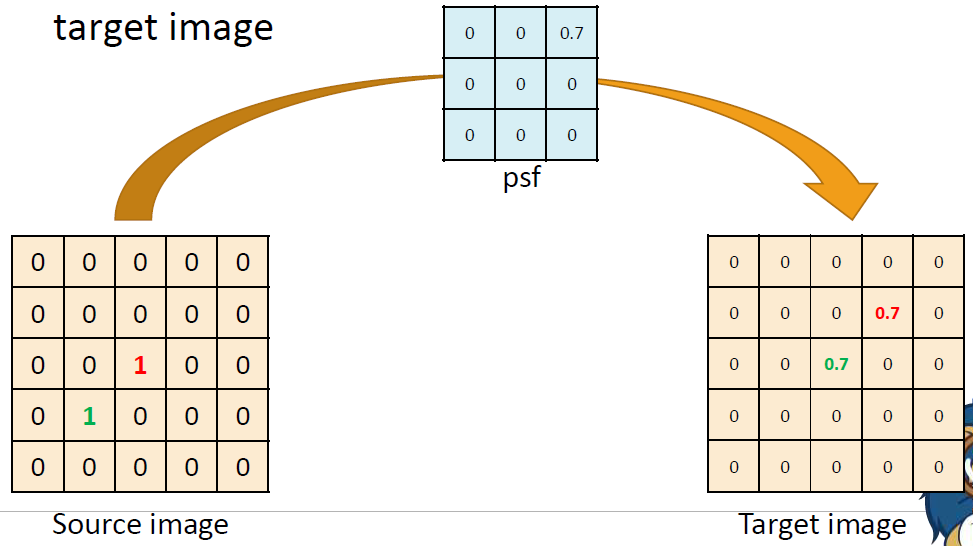 위의 경우에도 두 픽셀이 독립적으로
위의 경우에도 두 픽셀이 독립적으로 psf를 적용하고 있다.
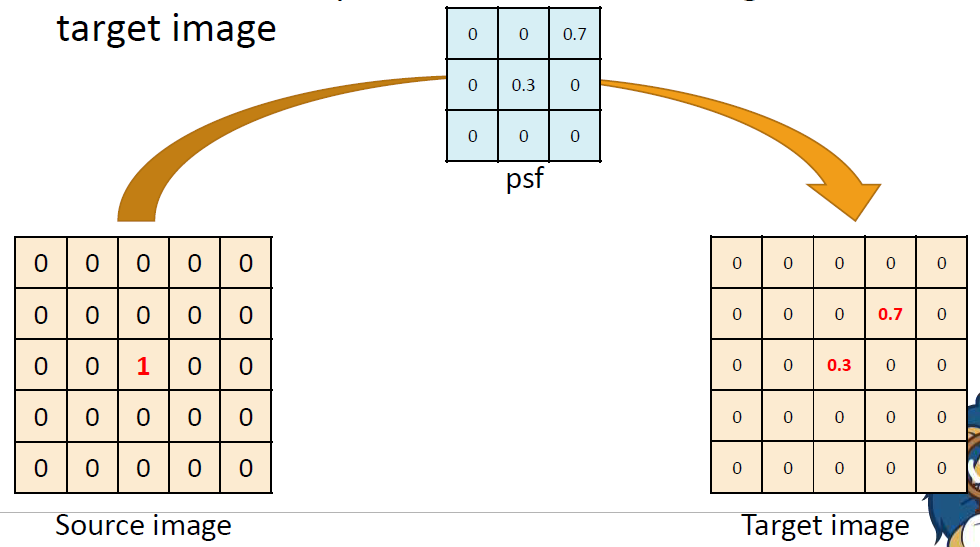 결국 weighted-sum이기 때문에
결국 weighted-sum이기 때문에 (source image value) * 0.3을 한 값이 가운데에 남고 (source image value) * 0.7을 한 값이 오른쪽 위로 옮겨지게 된다.
말 그대로 가운데 pixel의 값 중 일부가 오른쪽 위로 spread되었다.
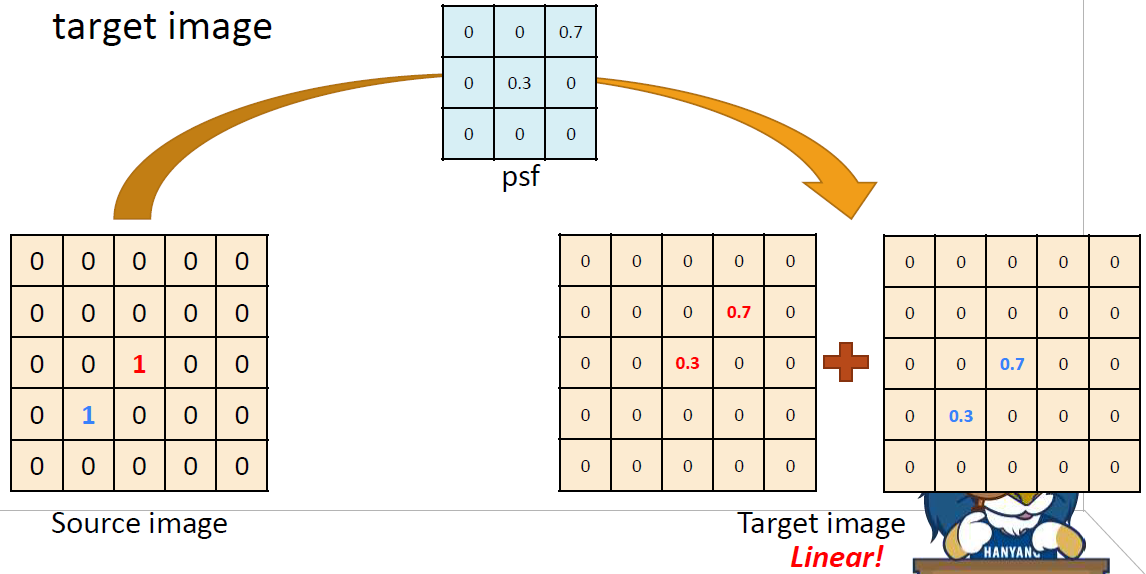 source image에서
source image에서 0이 아닌 값을 가진 pixel이 여러개이면 psf를 각 pixel들에 대해 독립적으로 적용해서 그 결과값을 서로 더한다.
psf를 사용하면 pixel의 내용이 spread되므로 spread된 결과를 하나씩 구해서 더하면 된다.
결과는 다음과 같다.
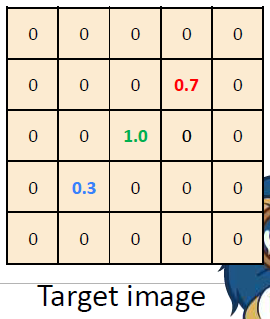
Convolution
source image를 H, target image를 G, psf를 F라고 하면 convolution의 식은 다음과 같다.
G = H * F (* 는 convolution operator)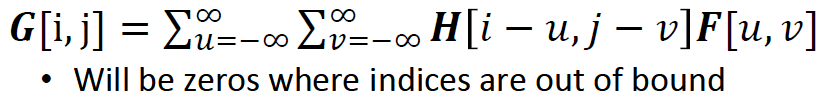 그런데 convolution은 cross-correlation을 통해 나타낼 수 있다.
그런데 convolution은 cross-correlation을 통해 나타낼 수 있다.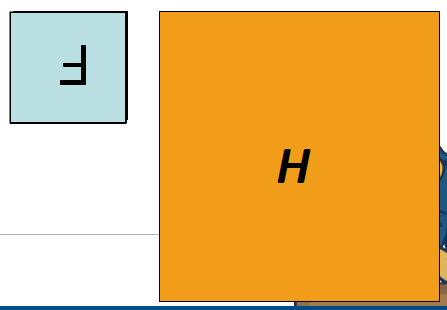 filter
filter F를 상하좌우로 뒤집어서 H의 모든 pixel에 대해 cross-correlation하면 그 결과가 convolution이 된다.
Cross-Correlation
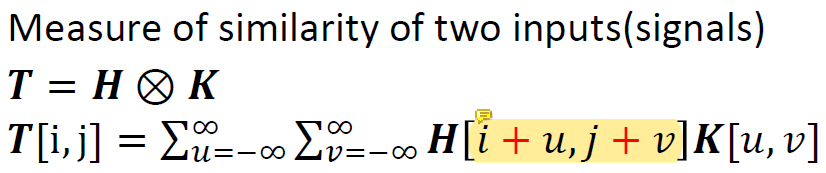 convolution에서
convolution에서 -가 +로 바뀐 차이만 있다.
cross-correlation은 weighted sum이기 때문에 cross-correlation을 사용하면 주변의 값을 더하는 것 만으로도 convolution을 수행할 수 있다.
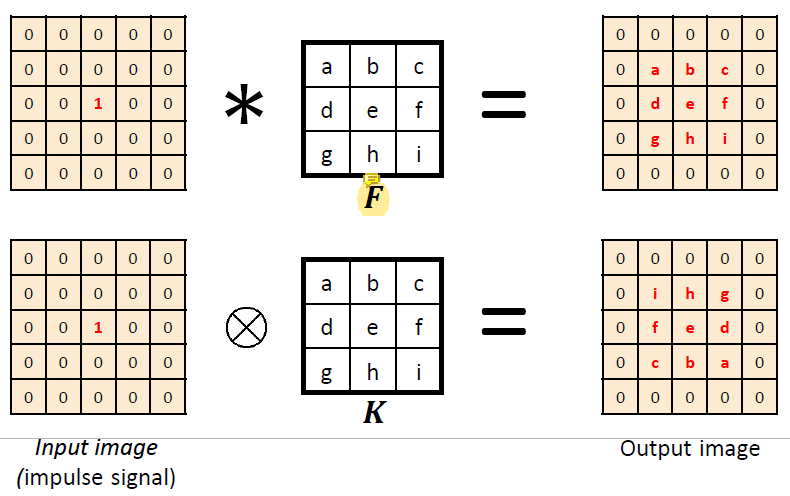 가운데의 같은 점에 filter를 적용했을 때 convolution은 필터 값이 그대로 나오고 cross-correlation은 상하좌우가 반전된 결과를 낸다.
가운데의 같은 점에 filter를 적용했을 때 convolution은 필터 값이 그대로 나오고 cross-correlation은 상하좌우가 반전된 결과를 낸다.
따라서 filter를 상하좌우로 반전시켜서 cross-correlation을 수행하면 convolution과 같은 결과를 낼 수 있다!
입력 image와 filter image가 비슷할수록 convolution의 결과값이 커진다.
Box Filter
box filter를 통해 denoising을 하는 경우를 생각해보자.
그림에서 noise를 제거하고 싶을 때는 많은 image를 가져와서 average를 사용하면 효과를 볼 수 있지만 optimal은 아니다.
만약 image가 한 개밖에 없다면 한 위치의 픽셀에서 그 주변의 local data의 average를 취하기도 하는데 이를 box filter라고 한다.
결국 weighted sum을 하는건데 box filter는 average를 취하는 weighted sum을 하는 것.
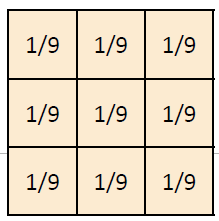 box filter는 symmetric한데 이와 같이 filter가 symmetric한 경우에는 convolution과 correlation의 결과값이 같다.
box filter는 symmetric한데 이와 같이 filter가 symmetric한 경우에는 convolution과 correlation의 결과값이 같다.
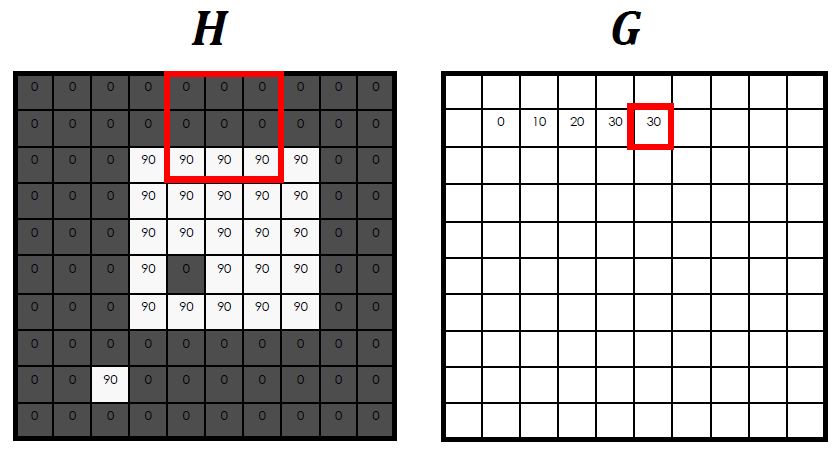 box filter를 적용하는 방법은 위와 같다. box filter가
box filter를 적용하는 방법은 위와 같다. box filter가 (3x3)이므로 적용할 pixel을 중심으로 (3x3)영역을 잡고 filter를 그대로 적용시켜주면 된다.
H에서 (3x3)영역의 각 pixel을 A, B, ..., I라고 할 때, 원래는 A*(1/9) + B*(1/9) + ... + I*(1/9)를 수행하는 것이 정석이지만 어차피 box filter는 평균을 구하는 것이기 때문에 (3x3)영역의 모든 값을 더해서 평균을 낸 값이 output이 된다.
위의 그림에서는 (90+90+90) / 9 = 30이 결과값이 되었다.
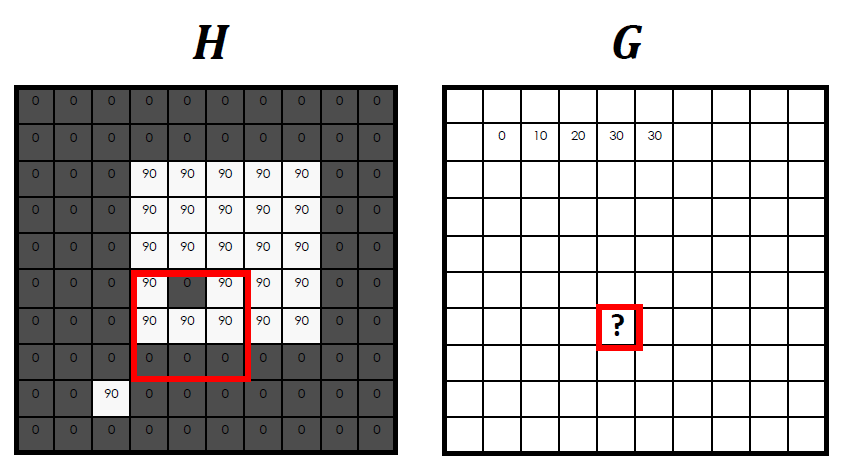 같은 방법으로
같은 방법으로 ?안에 들어갈 값은 (90*5) / 9이기 때문에 50이다.
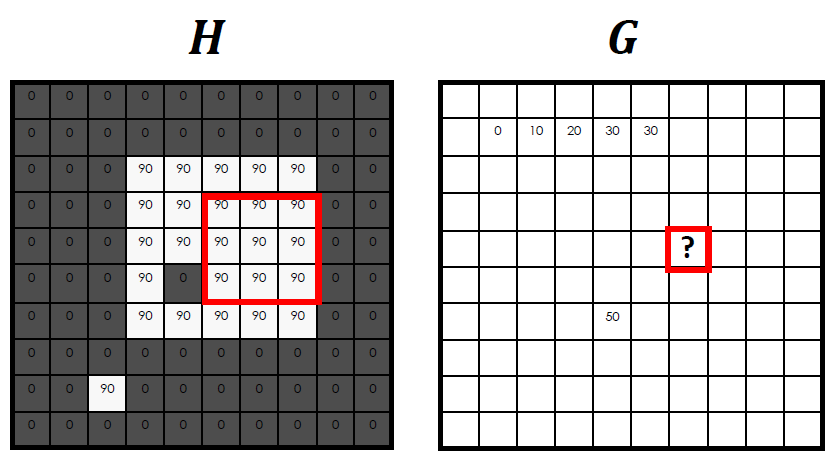 동일하게
동일하게 ?안에 들어갈 값은 (90*9) / 9이기 때문에 90이다.
이렇게 box filter를 모두 적용하고 나면 다음과 같은 결과가 나온다.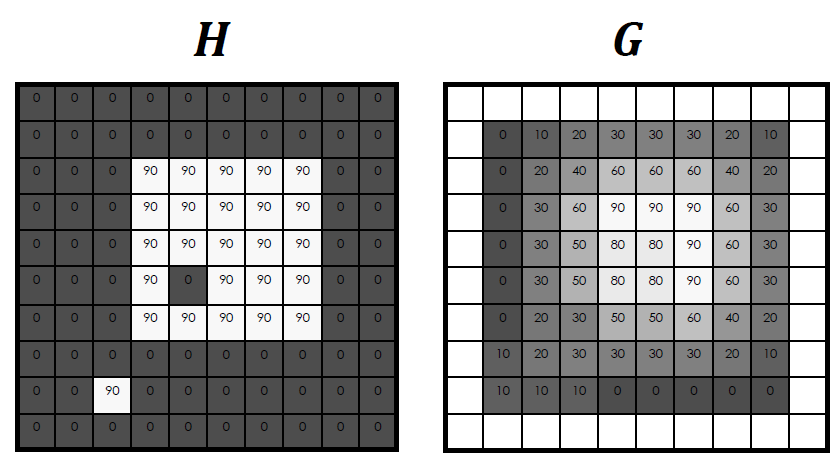 denoising을 위해 주변 pixel들의 평균을 취했고 훨씬 smooth한 output을 얻었다.
denoising을 위해 주변 pixel들의 평균을 취했고 훨씬 smooth한 output을 얻었다.
하지만 smooth한 결과로 인해 blurring된 결과를 얻었다.
filter의 sum이 1인 이유는 filter를 적용하고 난 뒤에 남는 data의 양을 일정하게 유지시켜주기 위해서이다.
만약 filter의 총 합이 0.1이라고 생각해보자. filter를 적용하고 나면 처음에 해당 영역 안에 존재했던 data의 양의 1/10밖에 남지 않게 된다. 따라서 원래 source image에서 해당 영역 안에 존재했던 data의 양을 output에도 동일하게 만들기 위해서 filter의 총합은 항상 1로 유지한다.
convolution은 이외에도 그림의 feature를 뽑아내는 등의 목적으로 사용할 수 있다.
Convolution Properties
convolution은 operator이기 때문에 아래의 properties가 적용된다.
- Commutative :
a * b = b * a - Associative :
a * (b * c) = (a * b) * c - Distributes over addition :
a * (b + c) = (a * b) + (a * c) - Scalars factor out :
ka * b = a * kb = k(a * b) - Identity :
Impulse e = [0, 0, 1, 0, 0], a * e = a
Padding
convolution은 image의 boundary에서는 정의가 되지 않는다. source image에서 filter 영역 만큼의 pixel 영역이 필요한데 boundary에서는 pixel의 수가 부족하기 때문이다.
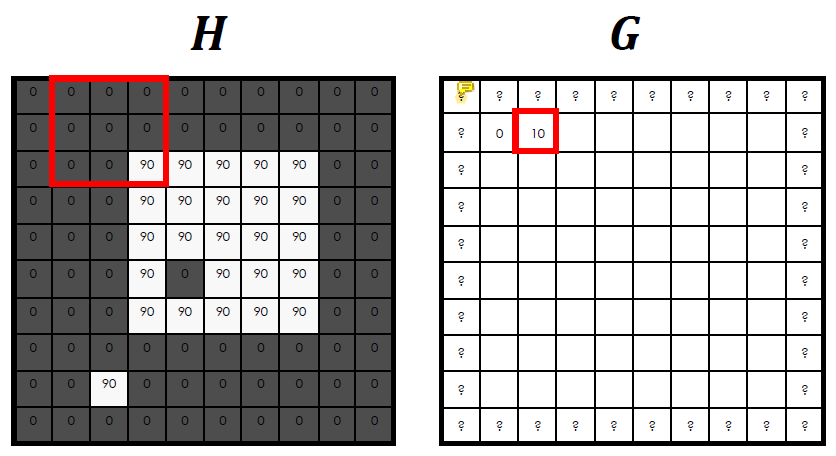 따라서 아예 input image를 키워서 convolution을 수행한다. 이렇게 이미지를 키우려고 끼워넣는 값을 padding이라고 한다.
따라서 아예 input image를 키워서 convolution을 수행한다. 이렇게 이미지를 키우려고 끼워넣는 값을 padding이라고 한다.
 padding은 여러가지 방법으로 가능하다.
padding은 여러가지 방법으로 가능하다. 0, 1, 0.5로 채울 수 있고 original image를 이용해 그 값을 copy하거나 변형해 사용할 수도 있다.
이 중 제일 많이 사용하는 것은 0으로 채우는 zero padding이다.
