Convolution

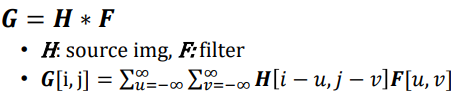2D convolution은 filter를 상하좌우 반전시킨 뒤 H의 모든 fixel에 대해 cross-correlation시킨 것과 결과가 같다.

CNN은 neural network의 각 node에서 적용되는 linear transformation -> non linear transformation에서 linear transformation으로 convolution을 적용한 것이다.
성능이 우수해 요즘에 많이 사용되고 있다.

convolution을 이용하면 굉장히 큰 size의 input을 다룰 수 있다는 장점이 있다.
input image가 매우 크면 그만큼 많은 perceptron이 존재하고 그에 따라 w, b도 매우 많이 존재한다. convolution을 사용하면 그 문제를 피할 수 있다.

또한 일반적인 neural network에서 64x64 resolution을 다루는 neural network를 만들었다고 가정하면 그 neural network에서 70x70 resolution은 다룰 수 없다. 그 크기에 맞는 linear transformation을 정의하지 않았기 때문이다.

하지만 convolution을 사용하면 입력 image의 resolution을 고려할 필요가 없다.
즉, input의 dimension이 fix될 필요가 없다는 것이다.

CNN은 이전처럼 w와 b를 구하는 문제가 아니라 convolution filter에 사용되는 각 값을 구하는 문제로 바뀌는 것이다. 즉, filter의 parameter를 구하는 것이 목표이다.

w*x+b를 쓰고 싶은데 linear convolution을 쓰면 filter에 사용된 값들을 learning해야한다.
그 값들이 정확하게 의미하는 바는 모르지만 그 값을 통해 loss function을 맞출 수 있다(loss function이 감소하도록).
만약 detect edge를 하기 위해 learning을 했는데 learning의 결과가 loss function을 맞추는 데에 도움이 안된다면 실제로 구한 값이 edge가 아니라 edge처럼 생긴 숫자 조합의 결과일 수도 있다.

Padding

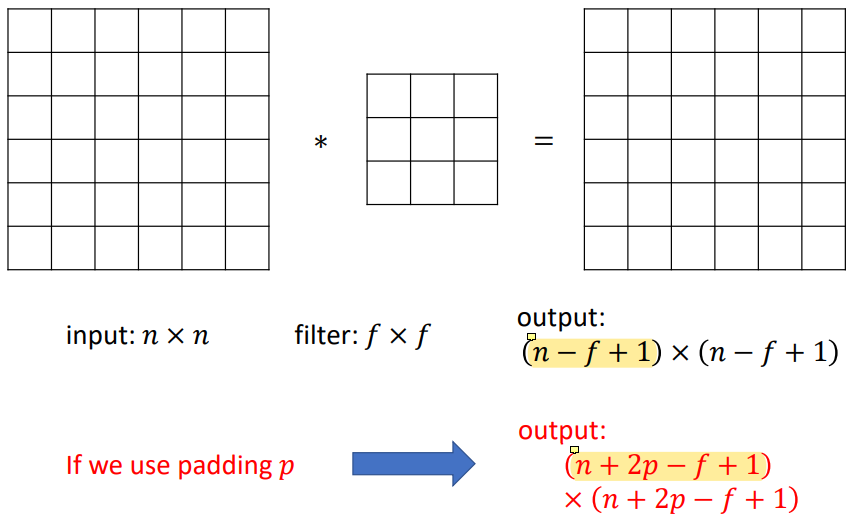convolution은 image의 가장자리에서는 정의되지 않기 때문에 그냥 convolution을 사용할 경우 output image size가 n-f+1로 줄어들게 된다.
하지만 padding을 사용하면 output size를 유지하거나 원하는 크기로 바꿀 수 있다.

Strided Convolution

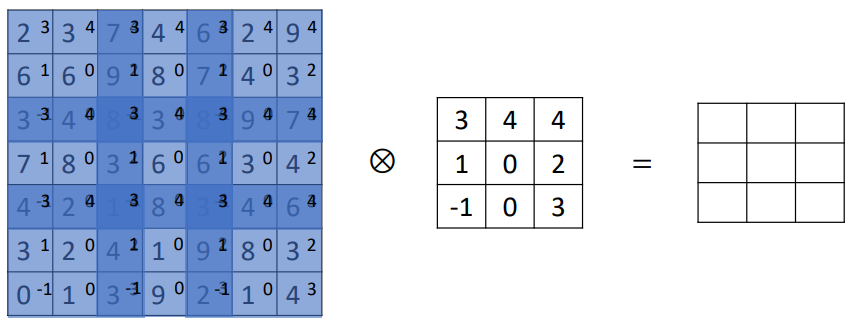strided convolution은 much smaller output이 나온다.
원래는 모든 pixel에 대해 convolution하는 것이 default,, 모든 pixel에 대해 filter 뒤집어서 cross-correlation하는 것이 default인데 strided convolution은 모든 pixel에 대해 convolution하지 않고 듬성듬성하게 convolution하는 것임. 두 픽셀 당 하나라던가....
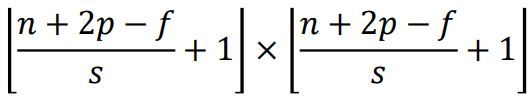stride가 1, 2, 3.. 일 때마다 그 값에 맞춰 s값을 조절하고 기본적으로 내림 연산을 한다(floor).

Summary Of Convolution

지금까지의 내용을 정리하면 다음과 같다.

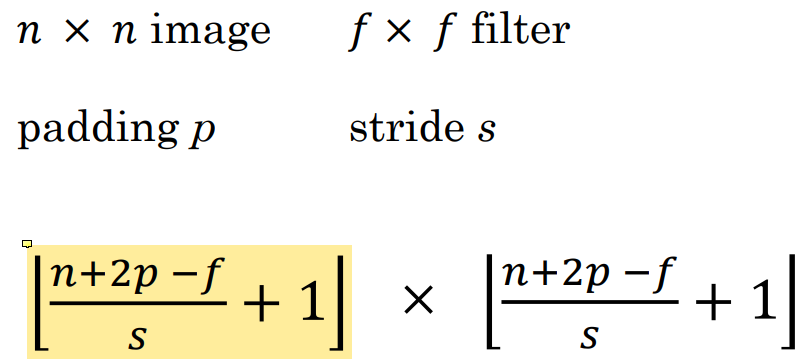
Convolutional Neural Network (CNN)

convolutional neural network는 CNN, ConvNet, DCN으로도 알려져 있다.

CNN은 local connectivity와 weight sharing으로 구성된 multi-layer neural network이다.

Local Connectivity

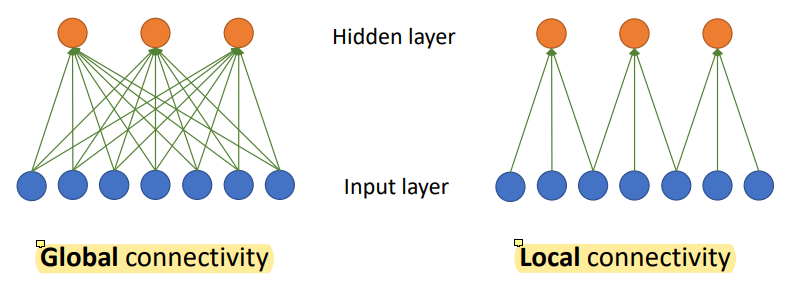global connectivity가 기존에 공부했던 방식이다.

7개의 temparature data, 3개의 hidden unit이 있으면 linear transformation으로 21개의 parameter가 생긴다.
w도 x를 따라 dimension이 7이 될거고 hidden unit이 3개니까 w는 7x3 = 21개이다.
input이 7개라 unit 하나에 w가 7개가 필요하고 unit이 3개니까 총 21개가 되는 것.

local connectivity는 입력을 전체 다 받는 것이 아니라 인접한 몇 개만 받는 형식이다.
몇 십일 전 data 말고 최근 것만 보고 동향을 알아내는 것과 비슷하다.
인접한 것, 가까운 것만 사용한다.

locally connect된것만 입력으로 받기 때문에 parameter의 수가 줄어든다.

Weight Sharing

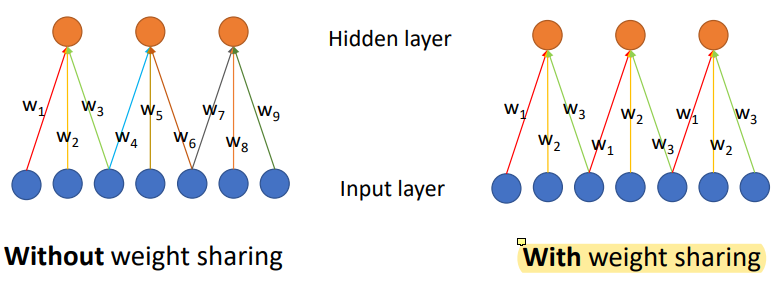인접한 몇 개만 weight를 따로 쓰고 나머지는 weight를 share한다. 그럼 parameter의 수를 한 layer 안에서 굉장히 많이 줄일 수 있다.

w1, w2, w3을 가진 vector 모든 영역에 적용된다.

CNN With Multiple Input Channels

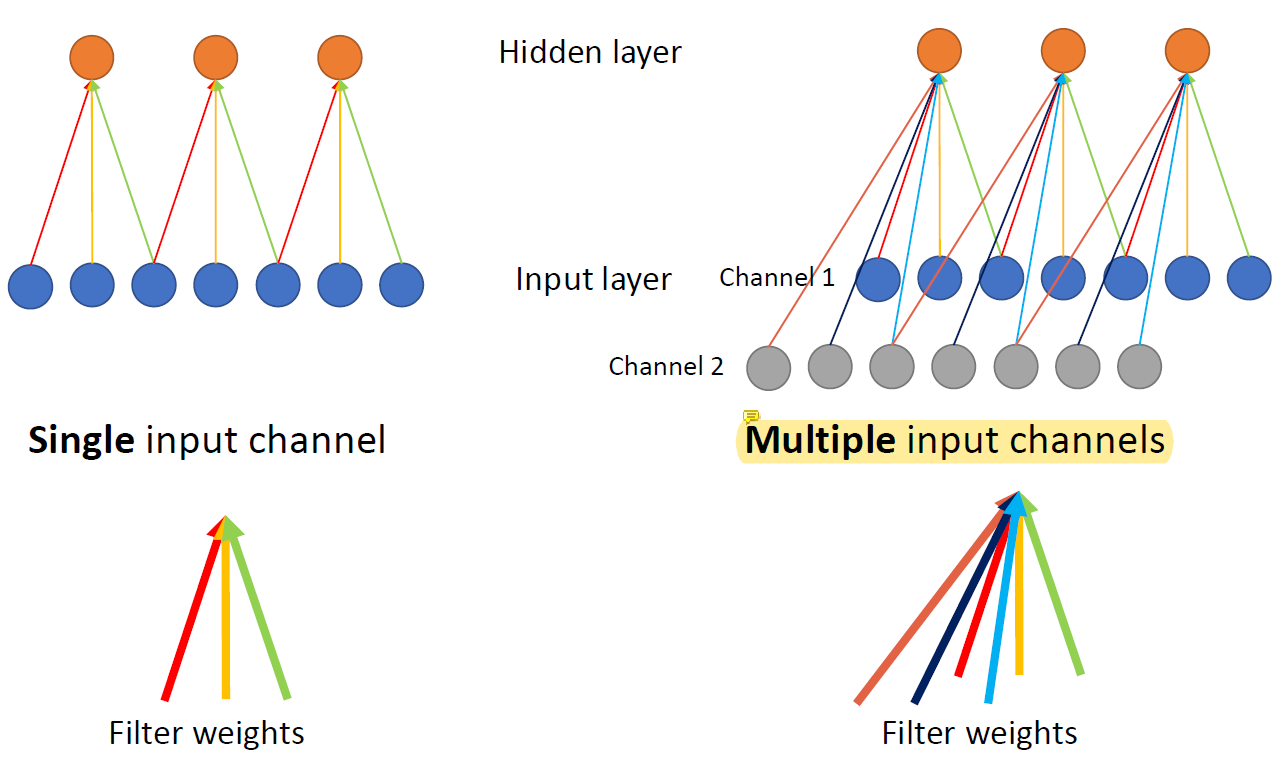RGB같은 것들이 channel을 의미하는데 channel이 여러 개여도 상관이 없다.
2D matrix가 여러 개 포개지면 channel이 되는 것이다.

보통 network 중간 단에 channel이 많은데 그것을 쉽게 다룰 수 있게 해준다. channel 마다 weight를 share할 수도 있고 channel 전체가 weight를 share할 수도 있다.

CNN With Multiple Output Maps

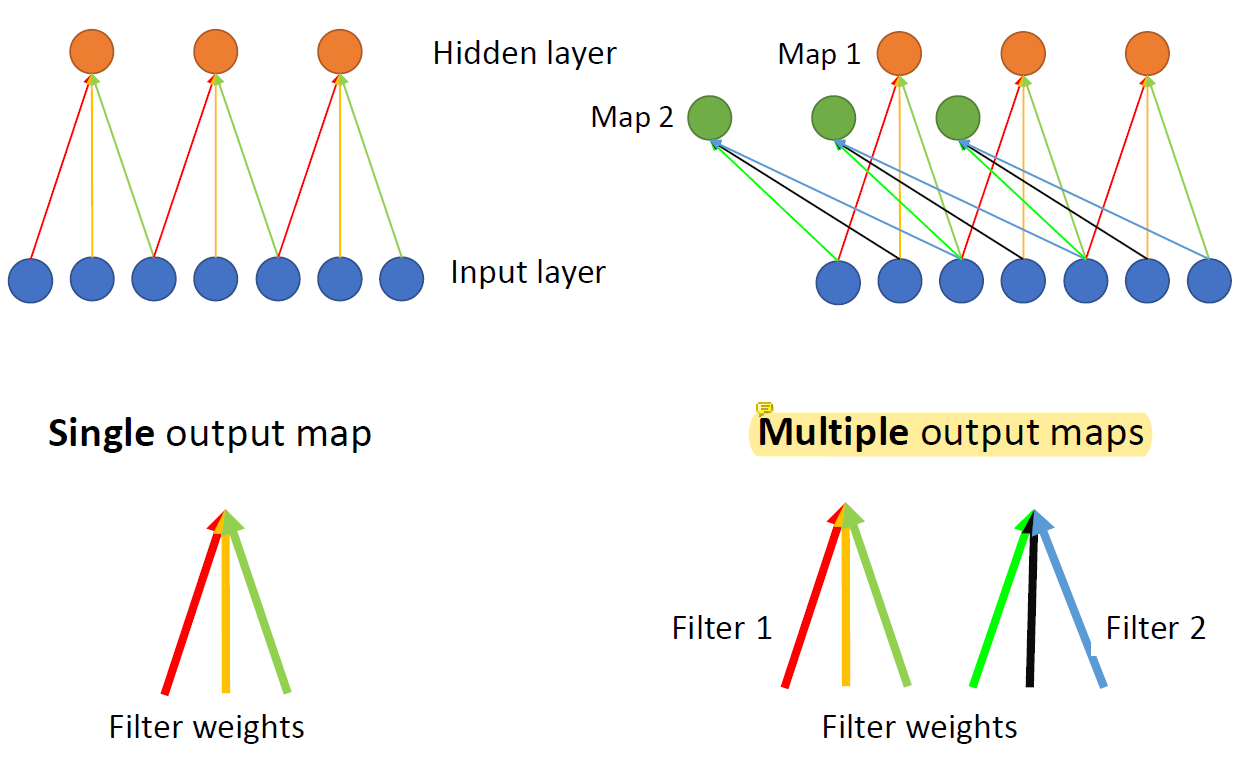multiple channel을 가진 input을 받을 수도 있고 input을 받아서 multiple channel로 만들 수도 있다.

이를테면 흑백 이미지로 color 이미지를 만들 수도 있다는 것.
hidden unit의 수와 parameter의 수를 늘리면 된다.

multiple channel을 multiple channel로 만드는 것도 가능하다.

Multiple Output Filters

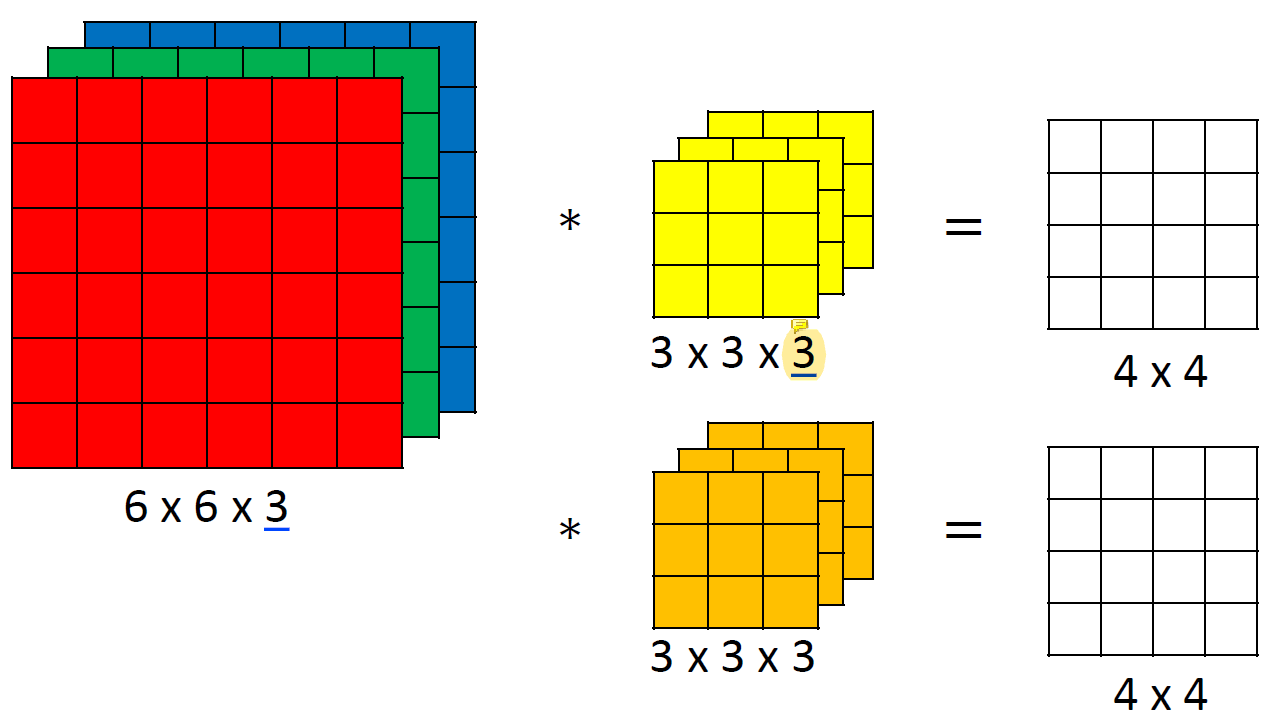
m channel input이 들어오면 convolutional filter의 channel도 m이어야 한다.

m channel input -> m channel convolution filter

채널이 여러 개면 그 채널을 다루는 필터도 여러개여야 한다.
각 채널마다 필터가 하나씩 있다. 그리고 그 채널마다의 결과를 모두 더해서 최종 dimension이 1이 된 것이다.

각 채널마다 필터 다 뒤집어서 cross-correlation한 결과를 전부 더해서 하나로!

만약 channel을 늘리고 싶다면 여러 개의 hidden unit을 사용하고 각 unit 안에서 linear, non-linear convolution을 사용하고 필터 개수를 늘려서 output channel을 늘릴 수 있다.

Example of a Layer

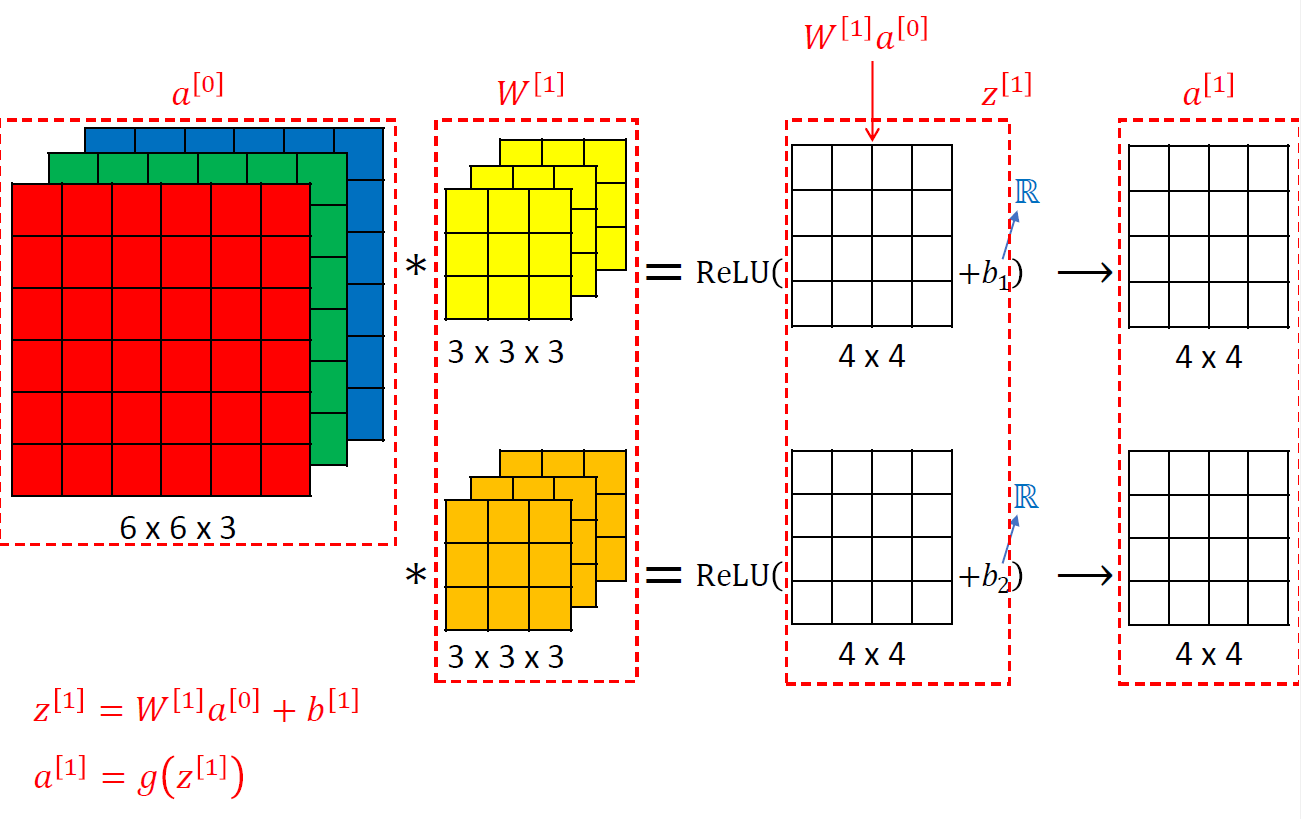
b는 실수 하나이다. linear이기 때문이다.

convolution을 한 번 하고 거기에 bias를 넣으면 z이고 그것을 activation function에 넣어준다.
여러 channel에 독립적으로 같은 작업을 수행하는데 대개는 activation function으로 ReLU를 사용한다.

Number of Parameters in One Layer

Neural network의 한 layer에 (3x3x3) 인 filter가 10개 있는 경우 해당 layer에는 몇 개의 parameter가 있을까?
-> 280개

10개의 (3x3x3) filter는 10 channel output을 가진다.
따라서 (3x3x3x10)개의 parameter가 필요하다.

bias parameter까지 고려하면 single channel에 대해 single bias parameter가 필요하므로 10개의 bias parameter가 추가적으로 필요하다.

따라서 최종적으로 필요한 parameter의 개수는 270개 for convolution, 10개 for bias 이므로 280개다.

위 network가 받을 수 있는 input channel의 개수는?
-> 3개

kernal의 마지막 dimension이 input의 dimension이기 때문에 (3x3x'3')으로, input이 3 channel, output이 10 channel이다.

위 network의 input image의 resolution은?
-> 무엇이든 가능

input의 가로세로 얼마짜리를 받을 수 있냐는 의미이다.
입력의 가로세로 자체는 중요하지 않다.

Convolution에서는 resolution의 제약이 없고 cross-correlation만 계산하면 된다.

하지만 기존의 (wx+b)는 image size가 고정이었다.
w size와 image size가 같았다.
w가 (100x100)이면 다른 size의 image를 받을 수 없었다.

w가 고정이기 때문에 x도 고정, 입력의 dimension이 고정이었다.

Summary of Notation

2D Convolution Layer

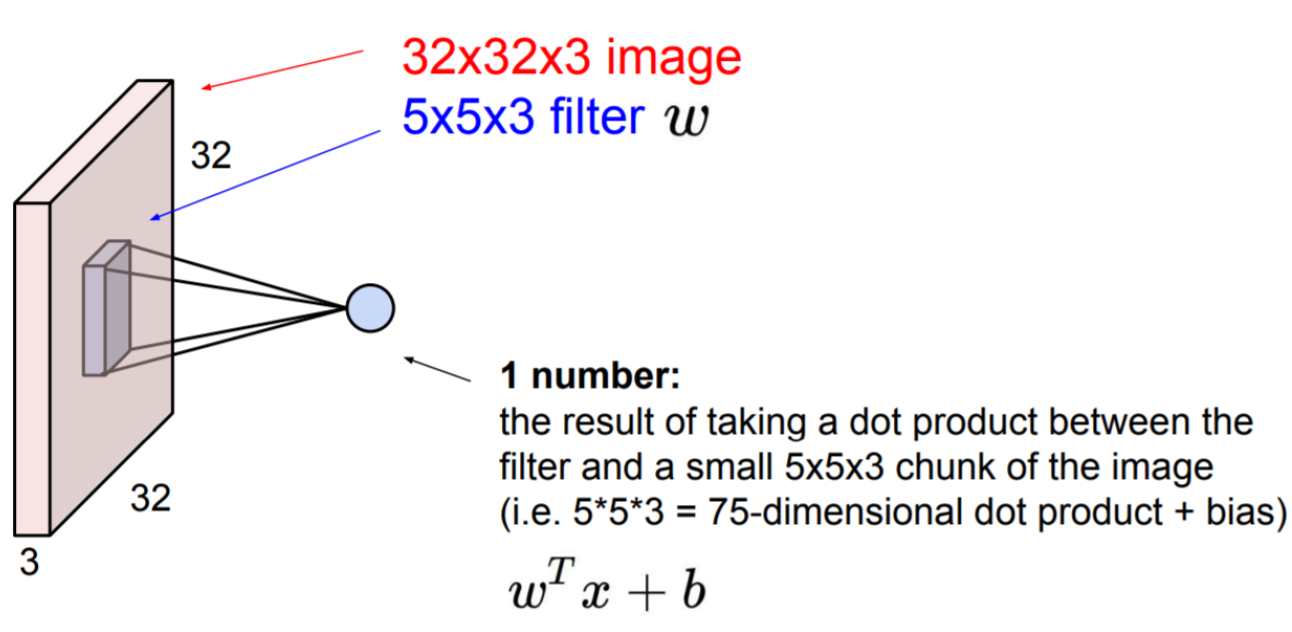
(32x32x3) image가 있다고 생각해보자.
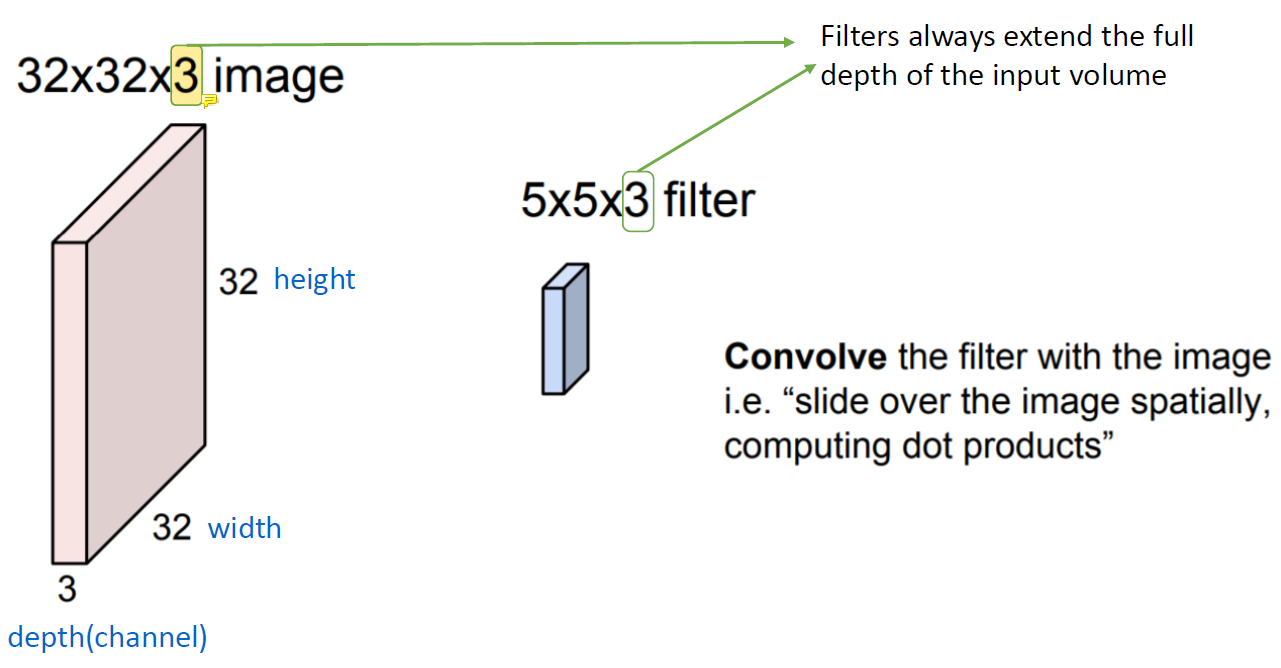Input image의 channel 개수와 filter의 channel 개수는 동일하다.
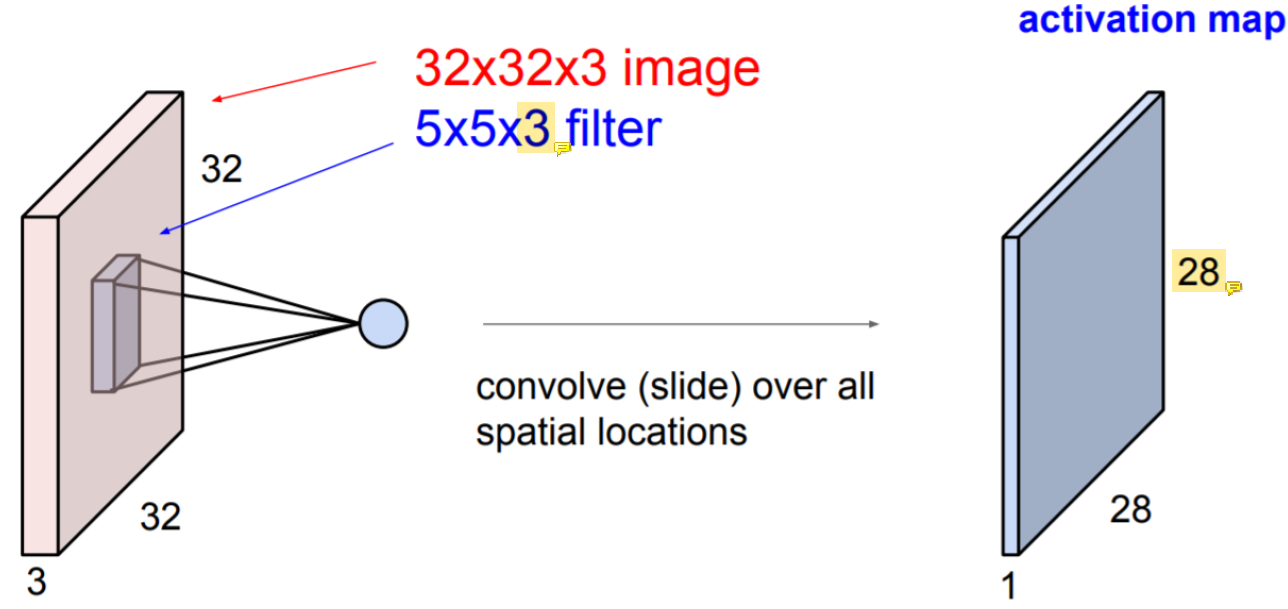Activation map에서 크기가 28로 줄어든 이유는 padding을 사용하지 않았기 때문이다.

또 다른 filter를 사용하면 이렇게 또 다른 activation map이 나온다.

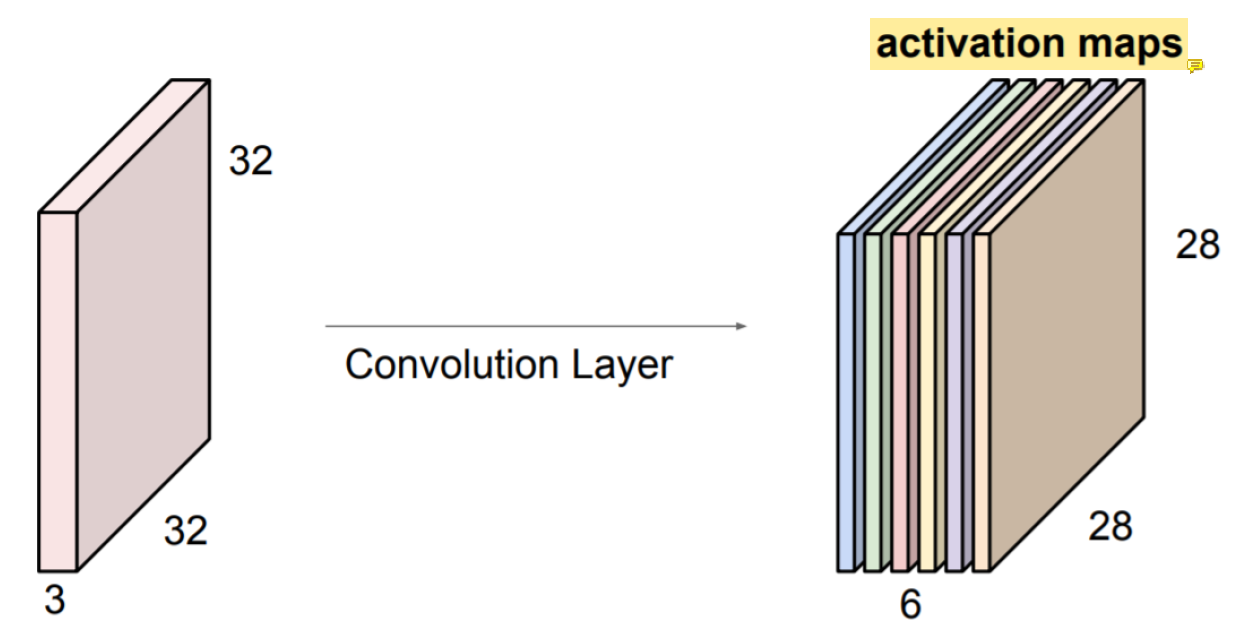
(26x26x6)의 새로운 image를 얻으려면 위의 과정을 반복해 쌓아 올려서 activation map을 만들어주면 된다.
여기서 activation map은 convolution하고 activation function까지 지난 결과이다.

ConvNet은 convolution layer의 sequence이다.

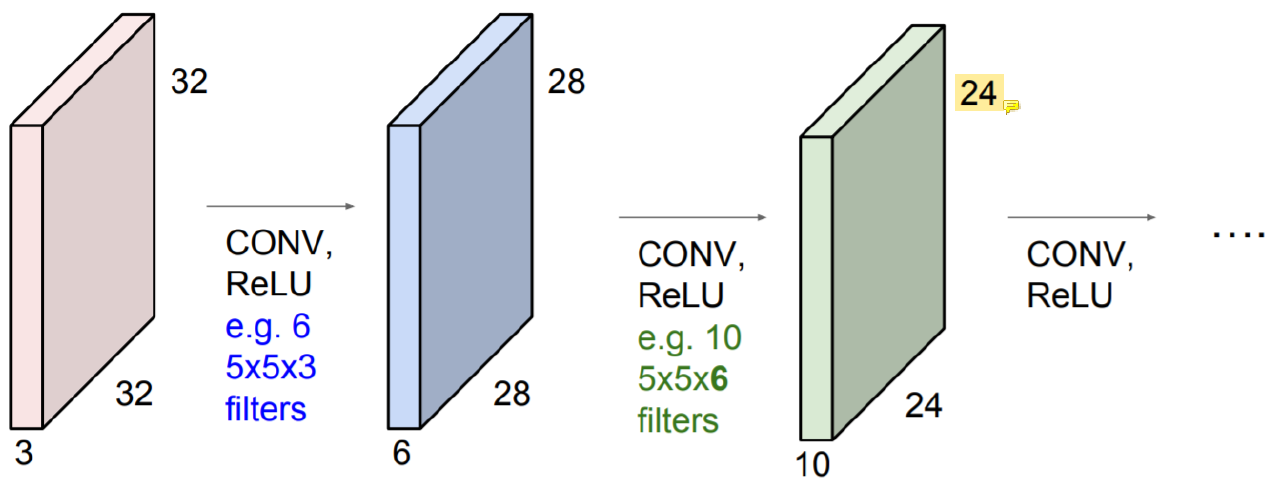
Example ConvNet

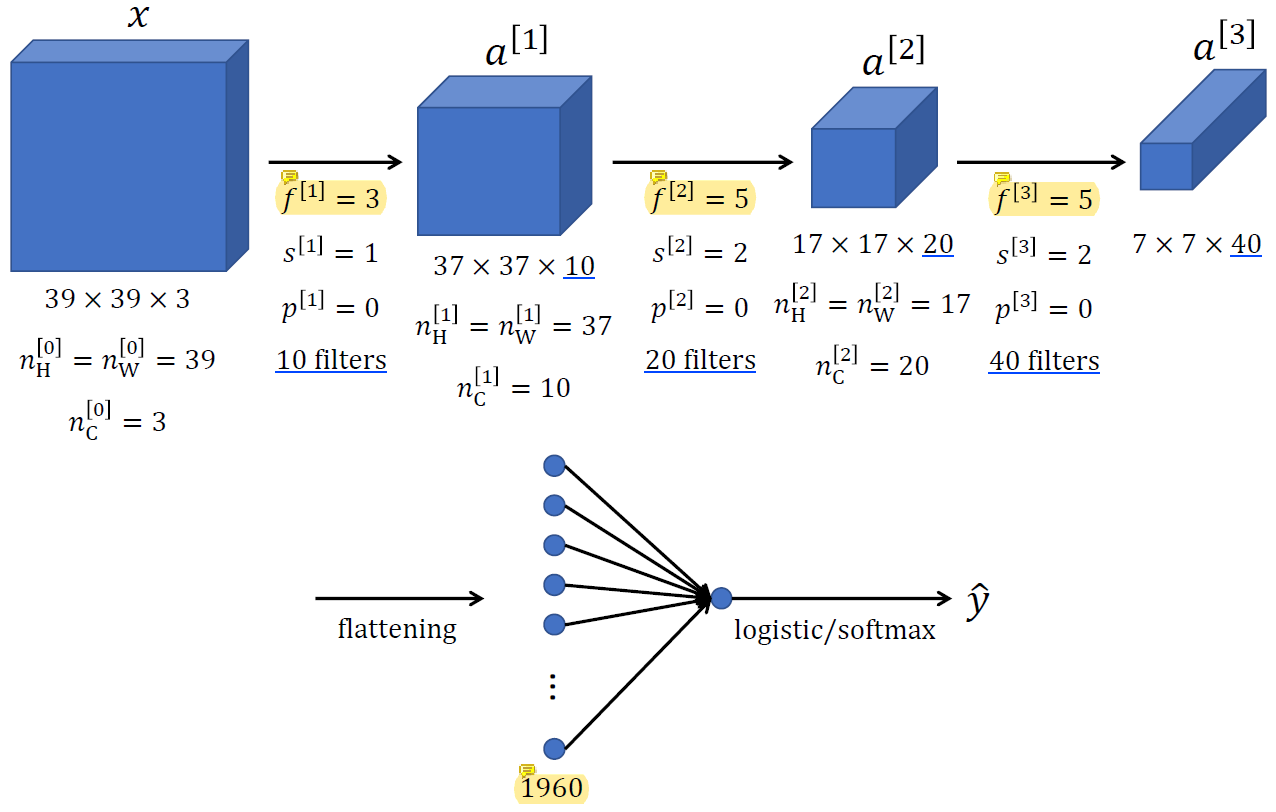
x에서 a[1]로 가는 과정을 보자.
x가 (39x39x'3')이기 때문에 (?x?x'3') 필터를 사용해야 한다.

한 필터 당 output으로 한 channel이 나오므로, a[1]이 10 channel이 되도록 만들고 싶다면 (3x3x3) 필터 10개를 사용하면 된다!

f[2]는 (5x5x10) filter, f[3]은 (5x5x20) filter가 된다.

a[3]에서는 (7x7x40) = 1960개의 feature를 가지고 최종 문제를 풀어야 한다.
이 feature들을 output layer에 넣을 때는 vector로 쭉 펴서 넣어주면 된다.

Pooling Layer: Max Pooling

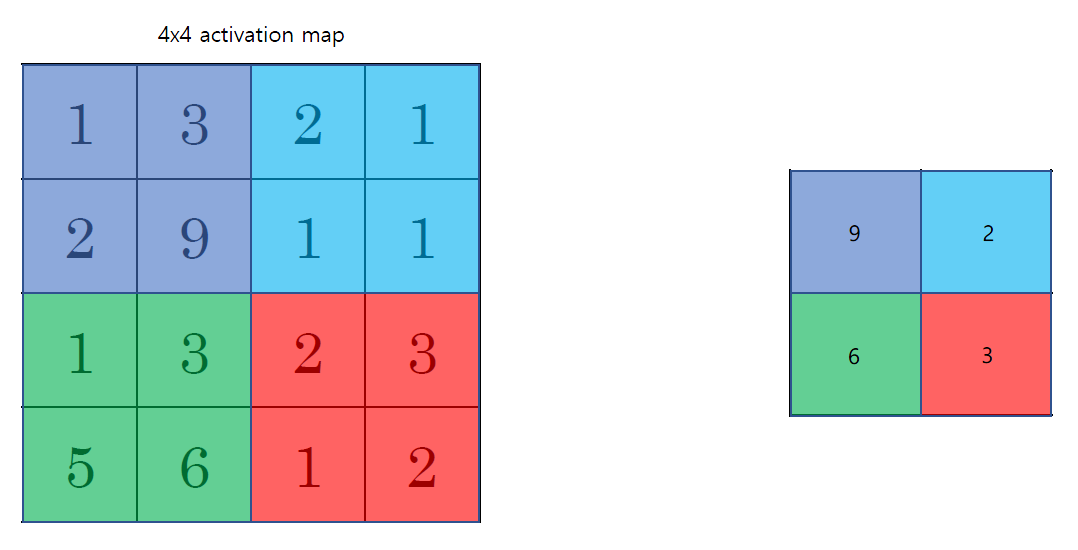Activation map에서 큰 값이 중요하다고 생각하고 그 값만 남기고 싶은 것이다.

ReLU에서 음수는 다 날렸지만 남은 양수 중 가장 큰 값이 중요하다고 생각해서 그 값만 남기고자 하는 것이다.

Pooling Layer: Average Pooling

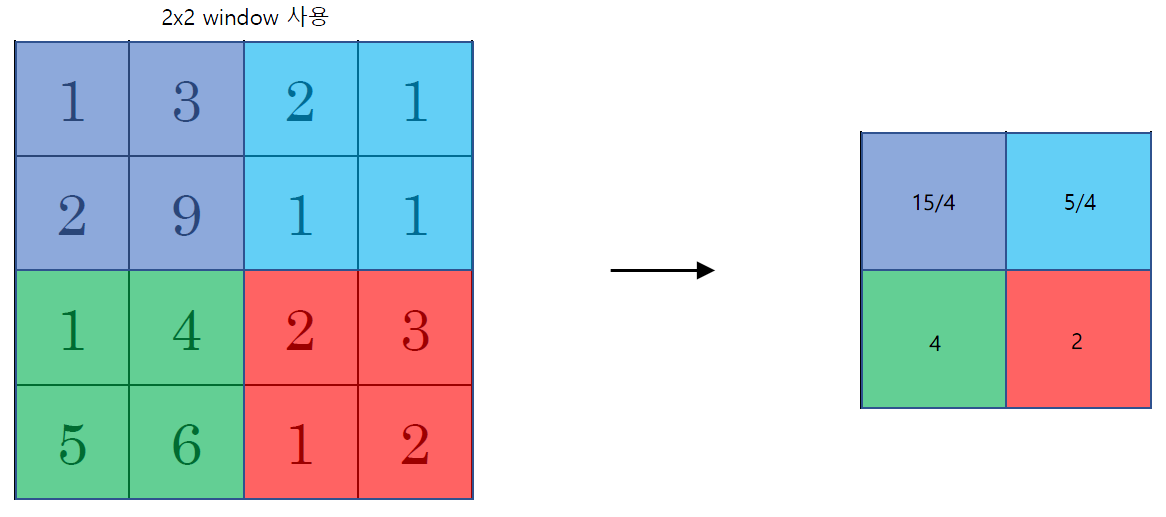Activation map을 가지고 average를 내는 건데 max pooling같은 경우에는 가장 큰 값이 중요하다고 생각했지만 average pooling은 영역을 대표하는 평균값이 중요하다고 생각하는 것이다.

둘 중 무엇이 더 좋을지는 써봐야 알지만 일반적으로 max pooling이 더 많이 사용된다.
Neural network의 중간 부분에는 max pooling이 선호되고 network의 끝으로 갈 수록 average pooling을 사용한다.

Pooling을 사용하면 보통 이렇게 activation map의 크기가 줄어든다.
Stride convolution에서도 stride 때문에 resolution이 줄어들었다.

Stride convolution과 pooling의 차이점은 stride convolution에는 학습해야하는 parameter가 있는데 pooling에는 없다는 것이다.

Average 값을 구하는 filter는 있을 수 있다. Box filter같은 것..

Average pooling은 stride convolution으로 구현할 수 있는데 max pooling은 convolution으로 흉내내기 어렵다.

Average pooling과 stride convolution의 차이점은 stride convolution은 trainable한 parameter가 있다는 것이다.
Stride convolution을 사용하면 각 값에 곱해지는 weight의 optimal을 training으로 구할 수 있다.

반면 pooling은 weight가 fix되어 있고 모두에게 동일하게 주어진 그 weight가 optimal이 아닐 수 있다.
하지만 속도가 빠르다.

Summary of Pooling

Neural Network Example (Lenet-5)

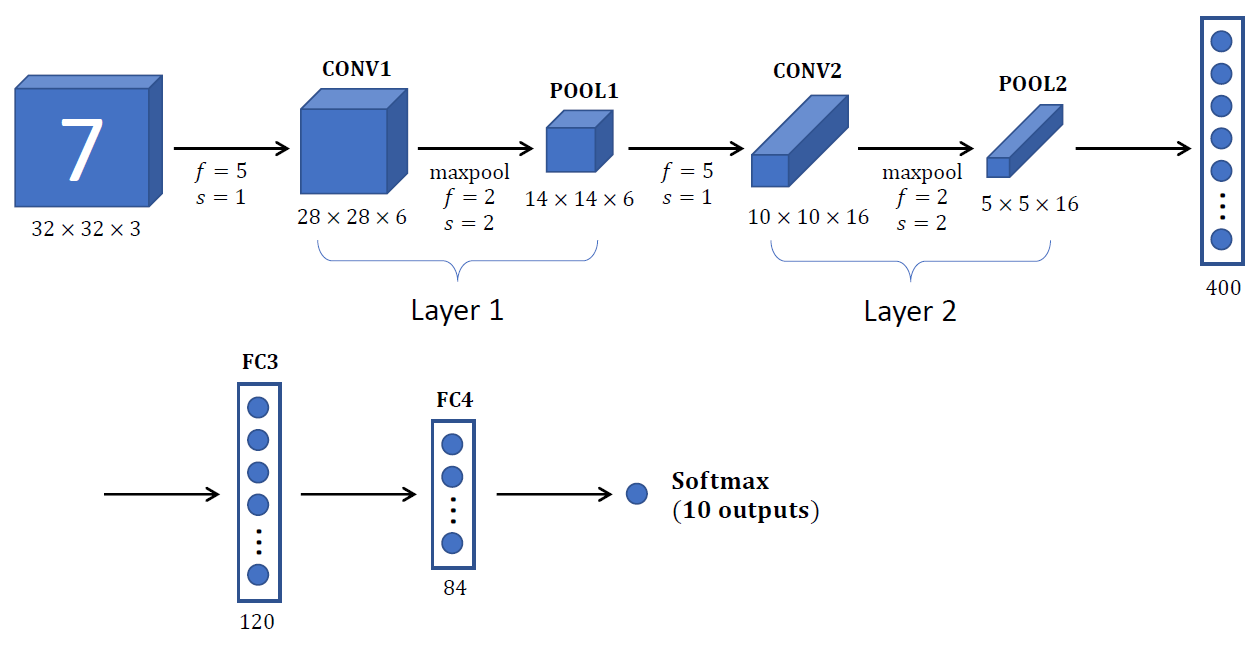
maxpool을 이용하고 있다.

Putting It Together

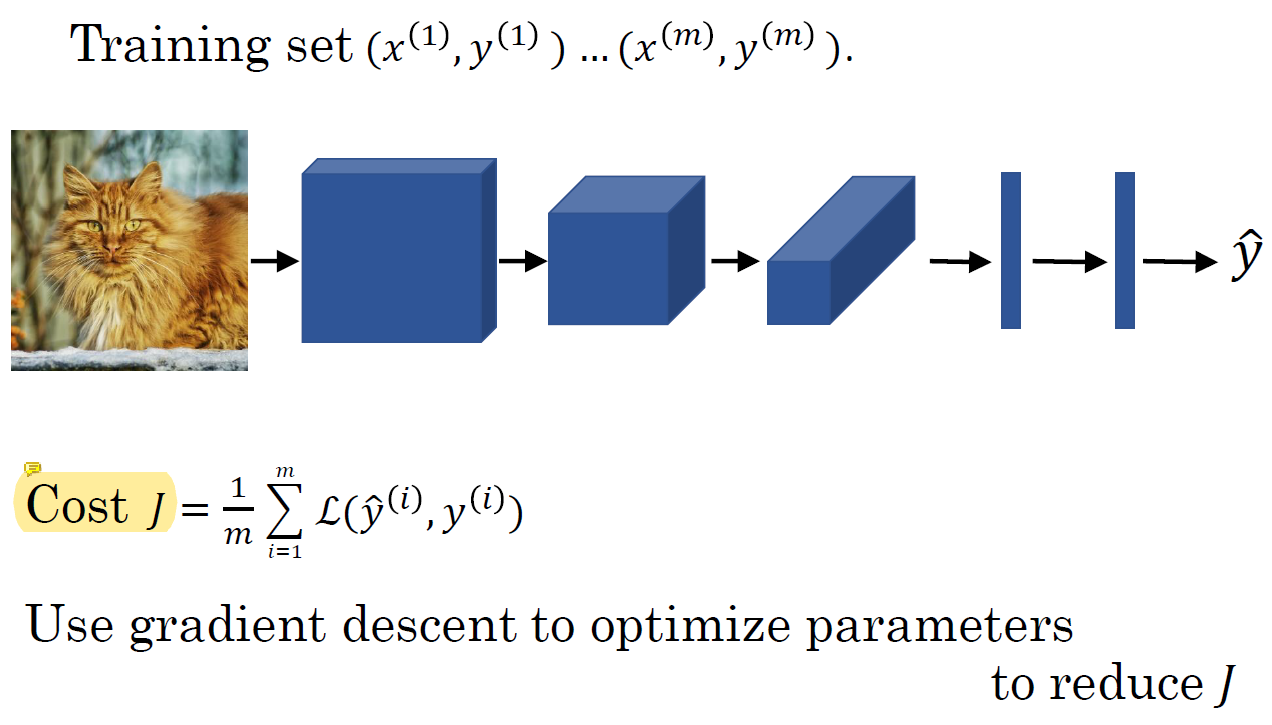Cost J에는 parameter의 gradient를 넣어서 계산한다.
J를 줄이기 위해 gradient descent로 parameter를 optimize한다.

Why Convolutions?

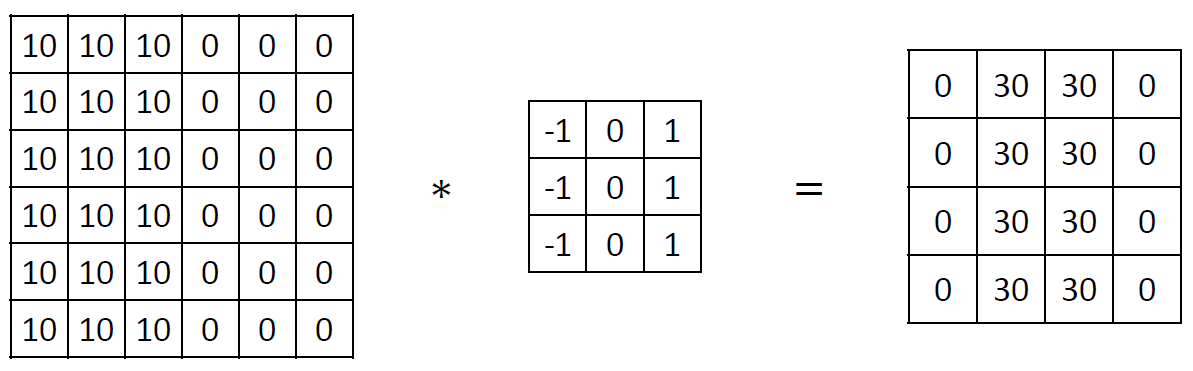Convolution을 사용하는 이유는 무엇일까?

1. Parameter sharing
   Parameter의 수를 줄일 수 있다.
   Vertical edge detector처럼 image의 한 부분에 useful한 어떤 feature detector가 image의 다른 부분에도 useful할 수 있다.

2. Sparsity of connections
   각 layer의 각 output 값은 적은 수의 input에만 의존한다.
   각 output에 영향을 미치는 input 사이의 관련성이 낮다는 의미!