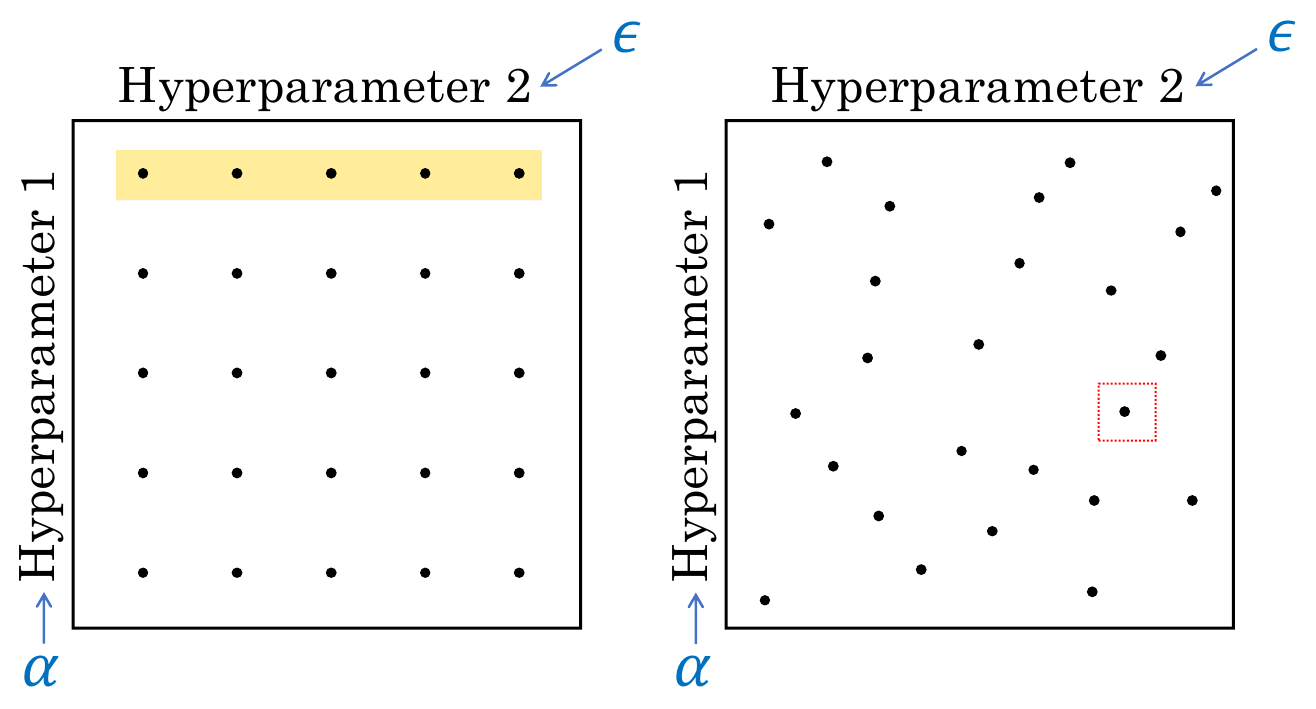
uniform하게 hyperparameter를 선택해서 그 중 좋은 것을 쓸 수 있지만 α입장에서는 그 α에 대해 다른 값을 5개밖에 보여주지 않은 것이 된다. 5개만 동일한 α에 대해 검사했기 때문에 보여주지 않은 값 중 더 좋은 것이 있었을 수도 있음..
랜덤하게 값을 선택해서 사용하면 α에서 더 많은 값을 검사할 수 있다. 하지만 운이 안좋으면 한쪽으로 sample이 몰릴 수 있다는 단점이 있다.
그래서 랜덤하게 선택한 값 중 제일 좋은 것을 써도 좋지만 그 주변을 다시 탐색해볼 수도 있다. 어찌됐든 직접 계산해보고 구하는거라 시간이 오래 걸린다.
naive하게 일정한 간격에서 α를 찾을 때 문제가 없는 경우도 있지만 hyperparameter의 물리적 특성을 고려해서 random sampling을 하면 더 좋은 결과를 얻을 수 있다.
learning rate는 작은 값을 가질 확률이 더 높기 때문에 log scale을 사용해서 작은 값일 때 더 집중적으로 검사를 수행하면 더 좋은 결과를 얻을 수 있다.
β = 0.9000이 β = 0.9005가 되는 것과 β = 0.9990이 β = 0.9995이 되는 것은 똑같이 0.0005차이지만 β가 클수록 평균을 구할 때 사용하는 sample의 수가 더 많다.
β = 0.9990일 때는 1000개의 sample을 더 사용하게 됐지만 β = 0.9000일 때는 10개의 sample을 더 사용하게 됐다. β입장에서는 똑같은 0.0005 차이인데 sample의 수 차이가 너무 심하다.
따라서 0.999 근처에서 β를 더 많이 검사해야 한다. log scale을 통해 β가 큰 쪽의 sample을 더 많이 검사한다.
