Computation Graph

model을 perceptron이라고 하는데 logistic regression에서는 loss function의 gradient를 통해 w와 b를 찾아야 한다.

코드로 gradient method를 구현할 때에는 최대한 효율적으로 계산해야하기 때문에 computation graph를 통해 계산한다.

J(a,b,c) = 3(a+bc) 라는 model이 있다고 가정해보자.
이 모델에서 input data는 a, b, c가 된다.

각 항을 쪼개서 새로운 문자를 사용해본다.

u = bc
v = a+bc = a+u
J = 3(a+bc) = 3(a+u) = 3v

이 상태에서 a = 5, b = 3, c = 2로 input이 주어졌다고 가정해보자. computation graph를 그리면 다음과 같은 형태가 된다.
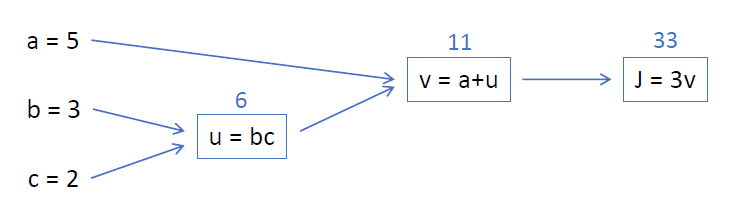gradient method는 결국 output인 J를 a, b, c에 대해서 미분한 값을 구하는 것이다.
따라서 최종적으로 dJ/da, dJ/db, dJ/dc를 구해야 한다.

input에 따라 forward pass를 하면 u = 6, v = 11, J = 33이 된다.

미분값을 구하기 위한 backward pass는 뒤에서부터 시작한다.

J = 3v에서 dJ/dv = 3임은 명확하다.

이를 통해 v = a+u에서 dJ/da를 바로 구할 수는 없지만 chain-rule을 이용하여 dJ/da = (dJ/dv)•(dv/da) = 3 * 1 = 3을 구해낼 수 있다.

이 과정을 보면 b와 c를 구할 때 dJ/du가 필요할 것임을 예상할 수 있다.
dJ/du = (dJ/dv)•(dv/du) = 3 * 1 = 3
위의 계산 결과를 이용해 dJ/db, dJ/dc을 구하면
dJ/db = (dJ/du)•(du/db) = 3 * c = 3 * 2 = 6
dJ/dc = (dJ/du)•(du/dc) = 3 * b = 3 * 3 = 9
를 구해낼 수 있다.

요약하자면 이전 stage에서 구한 gradient를 재활용해서 새로운 gradient를 구하는 방식으로 이것을 backpropagation이라고 한다.
최종 gradient는 dJ/da, dJ/db, dJ/dc이다. dJ/du와 같은 값들은 최종 goal에는 필요없지만 중간에 이용되는 값으로, 계산을 도와주기 위해 구해지는 값이다.

그렇다면 이런 형태의 computation graph는 어떻게 계산해야할까?
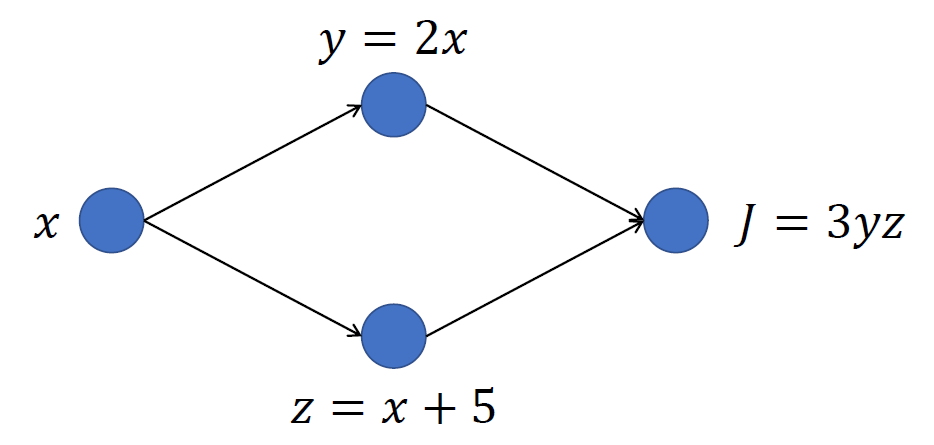위에서 본 computation graph와 다른 점은... 한 node에서 뻗어나가는 선이 2개라는 것이다.

쫄지 말고 그냥 계산하면 됨.. 이런 경우에는 위의 경로에서 구해지는 gradient 값과 아래의 경로에서 구해지는 gradient 값을 더하면 된다. dJ/dx을 구해보자.

J를 나타내는 식에서 문자가 y와 z로 2개이기 때문에 dJ/dx을 구하는 방법은 2가지일 것이다.dJ/dx = (dJ/dy)•(dy/dx)이거나, dJ/dx = (dJ/dz)•(dz/dx)이거나. 첫 번째의 경우 위의 경로를 이용하게 되고, 두 번째 경우에는 아래의 경로를 이용하게 된다.

1. dJ/dx = (dJ/dy)•(dy/dx) = 3z * 2 = 6z
2. dJ/dx = (dJ/dz)•(dz/dx) = 3y * 1 = 3y

이므로 최종적으로 dJ/dx는 두 값을 더해서 3y + 6z가 된다.

Logistic Regression Derivatives

logistic regression에서 어떻게 gradient descent를 구현하는지 살펴보자. a는 non-linear output이자 prediction의 결과이다.
loss function은 여러가지가 있을 수 있지만 cross-entropy loss를 사용해보자.

그럼 이러한 형태의 computation graph가 그려진다.
우리는 w와 b의 값을 조절해서 loss function의 값을 줄이고자 한다.
x와 w의 값이 2개인 이유는 x와 w모두 element가 2개인 2차원 벡터이기 때문이다.
logistic regression에서 z를 구할 때 선형변환, a를 구할 때 비선형변환을 하며 x는 고정된 input일 뿐이므로 구해야 할 값이 아니다. 따라서 결과적으로 dL/dw와 dL/db만 구하면 된다.

하지만 dL/dw, dL/db을 구하기 위해서는 중간 과정인 dL/da와 dL/dz가 필요할 것임을 예상할 수 있다.

dL/da를 da라고 부르기로 하자, 그럼 da = dL/da = -y/a + (1-y)/(1-a)가 된다.
비슷하게 dL/dz를 dz라고 부르기로 하면 dz = dL/dz = (dL/da)•(da/dz) = a-y가 된다.
이 계산을 끝내면 dL/dz(==dJ/dz)를 알고있으므로 구하고자 했던 dL/dw1, dL/dw2, dL/db 를 구할 수 있다.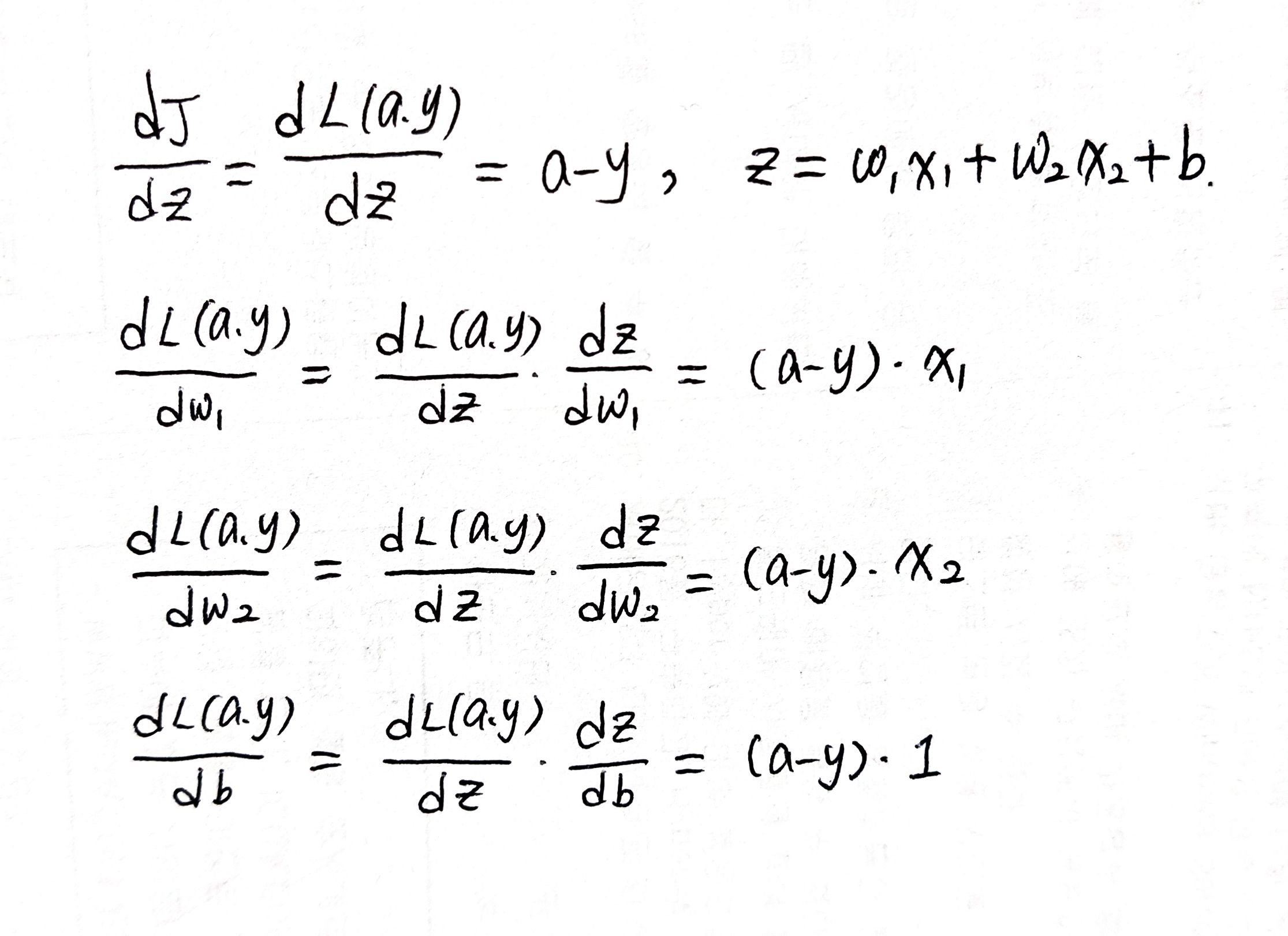이를 gradient method에 적용할 때는 w1, w2, b에 값에서 위에서 구한 dL/dw1, dL/dw2, dL/db에 일정한 learning rate α를 곱한 값을 빼서 update시켜주면 된다.

이를 m개의 example을 가지고 계산할 시에는 m개의 example에 대해 구한 미분값을 전부 더해 평균을 내서 사용해준다.
평균을 사용하면 gradient의 noise를 줄여주는 효과가 있다. 각 example에 대해서 모든 값이 정확하지 않을 수 있다.. 예를 들면 사진을 learning하는데 사진이 어두운 데에서 찍혔거나 흔들렸거나 하면 그 사진으로부터 나온 gradient값이 아주 정확하지 않을 수 있다. 이 때 엄청나게 많은 training data를 통해 구한 값의 평균을 내서 noise로 인해 생겼던 오차가 평균을 통해 어느정도 줄어드는 효과를 기대하는 것이다.
training data가 매우 많다면 그 수 많은 data의 경향을 모든 data가 어느정도 따라가게 되면서 noise가 줄어든다.