Neural Network

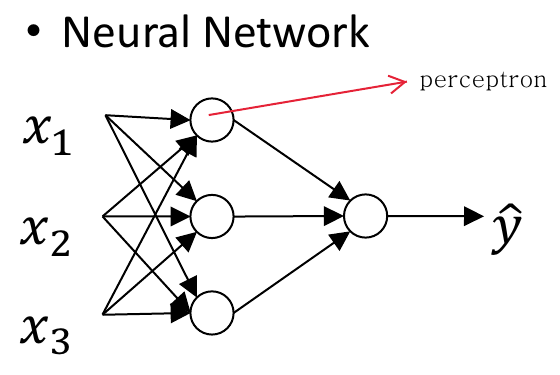이 그림과 같이 사람의 neuron을 본뜬 perceptron이 엮여있는 것을 neural network라고 한다.
저 그림에서 동그라미 하나가 perceptron에 해당한다.

인공지능에서는 스스로 생각할 줄 아는 컴퓨터를 만들기 위해 인간의 뇌를 구성하는 신경세포(뉴런)의 모양을 본따서 모델을 퍼셉트론으로 사용한다.

이 nerual network가 logistic regression이라면 저 퍼셉트론 하나에서 logistic regression 모델에서 수행하는 linear변환과 non-linear변환이 전부 일어난다.

이를 computation graph로 나타내면 다음과 같은 형태가 된다.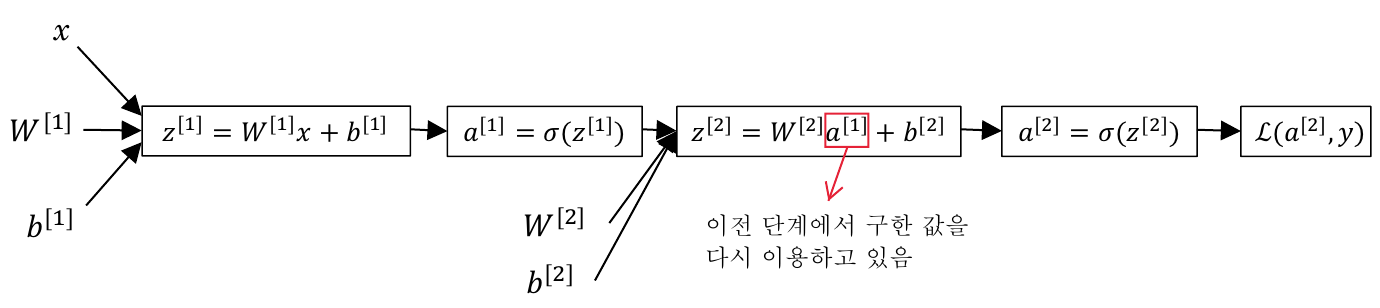[i]는 i번째 layer를 의미하고, (i)는 i번째 training sample을 의미한다.
computation graph를 보면 1번재 layer에서 구한 결과값(a[1])이 2번재 layer에서 사용됨을 확인할 수 있다.

Neural Network Representation

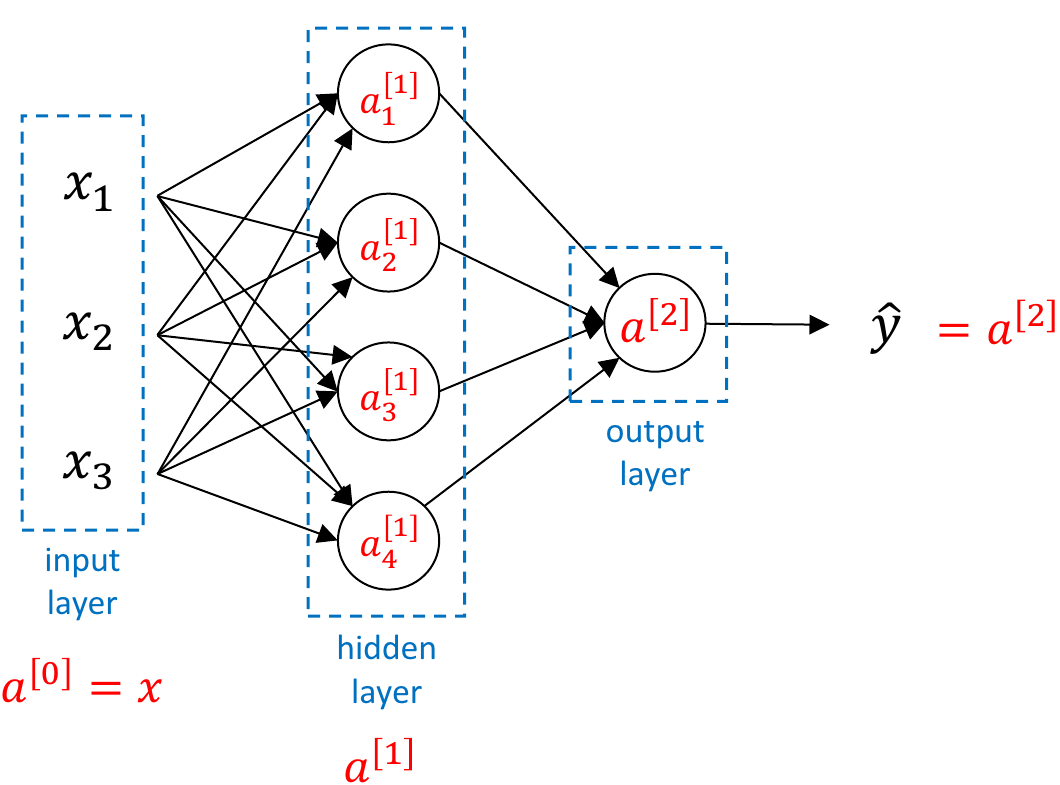위 그림의 nerual network는 2 layer neural network이다. input layer는 세지 않는다. input layer에는 변수가 없기 때문이다.
hidden layer은 결과값을 위한 중간 계산은 하지만 결과값이 무엇인지는 모르기 때문에 hidden layer라고 부른다.

그림에서 a[1]은 1번째 layer의 모든 a값을 합친 것으로 input이 4개인 4차원 벡터가 된다.

위 그림에서 1번째 layer의 모든 w를 모아 transpose한 것을W[1]이라고 하고 1번째 layer의 모든 b를 b[1]이라고 하자.

linear변환을 해야하기 때문에 한 퍼셉트론에 들어오는 input의 개수가 3개라면 w도 같은 수만큼 필요하므로 3개의 w element가 필요하다. 그리고 1번째 layer에 총 4개의 퍼셉트론이 존재하므로 W[1]은 (4,3)의 차원을 갖는다.
b는 scalar값이고 한 퍼셉트론 당 1개의 값이 필요한데 1번째 layer에 퍼셉트론이 총 4개이므로 b[1]은 (4,1)의 차원을 갖는다.

그림으로 좀 더 확실하게 dimension을 따져보자.
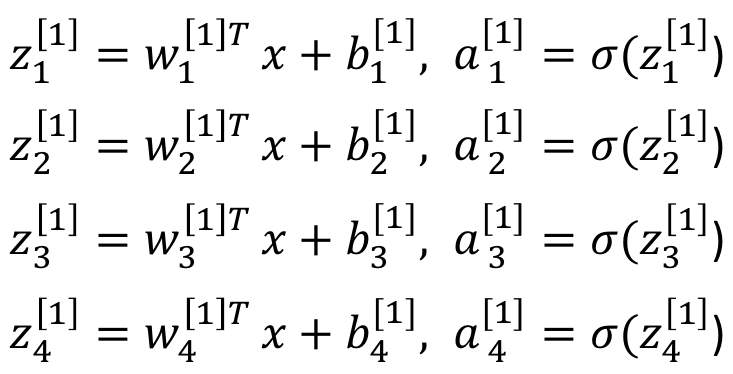이 그림에서 w1[1]은 input의 개수만큼 w가 필요하므로 (3,1)의 차원을 가질 것이다. 그런데 총 4개의 퍼셉트론이 존재하므로 w[1]은 (3,4)이다. 그런데 선형변환을 위해서는 transpose를 해야하므로 w[1]T는 (4,3)이다.
총 input이 3개이므로 x는 (3,1)이기 때문에 w[1]Tx를 수행하면 (4,1)의 차원이 된다.
b는 각 퍼셉트론 당 1개씩 있고, 퍼셉트론이 총 4개이므로 (4,1)의 차원을 가져 결론적으로 z[1]은 (4,1)이 될 것이다.
a[1]은 non-linear transpose이고, 앞서 계산한 linear transpose를 통해 나온 결과값이 scalar였으므로 non-linear transpose를 해도 그 결과값은 scalar이다. 따라서 z[1]과 동일하게 (4,1)의 dimension을 갖는다.

이 결과를 통해 2번째 layer를 계산해보면
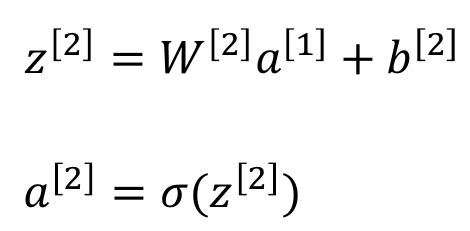2번째 layer의 퍼셉트론 하나에 대해 input이 4개이고, 퍼셉트론이 하나이므로 (4,1)이고, transpose하면 W[2]는 (1,4)이다.
위에서 a[1]이 (4,1)이었으므로 W[2]a[1]은 (1,1)이다. 거기에 (1,1)인 b[2]를 더한 z[2]는 (1,1)이다.
z[2]를 넣어 non-linear변환을 한 a[2] 역시 (1,1)일 것이다.