생성모델(Generation Model) 이란?

출처

생성모델(Generation Model) 이란?

• 생성 모델(Generative Model)은 주어진 데이터로부터 새로운 데이터를 생성할 수 있는 기계 학습 모델입니다.

• 이러한 모델은 데이터의 근본적인 구조를 학습하여 새로운 샘플을 생성하거나 기존 데이터를 확장하는 데 사용됩니다.

  • 생성 모델은 여러 유형이 있으며, 주요 목적은 무작위한 입력(예: 노이즈와 같은)을 받아들이고 여기에 기반하여 현실과 유사한 데이터를 생성하는 것입니다.

Machine Learning/Deep Learning의 발전이 급격히 이루어지면서 다양한 인공지능 모델이 연구되고 만들어지고 있습니다.

• 최근에는 OpenAI의 GPT-3, NAVER CLOVA의 HYPERCLOVA등 거대 AI모델들이 출연하고 있습니다.

필자는 이런 모델들을 연구하고 공부하면서 이 모델자체를 어떻게 분류하는게 맞는가 하는 고민을 항상 같이 합니다.

• 예를 들어 어떤 모델을 사용하면 이 모델 자체를 분류모델로 보는것이 맞나? 생성모델로 보는것이 맞나? 라는 질문을 스스로 계속합니다.

  • 사실, Pre-Trained 된 모델을 이용하여 다양한 Downstream Task에 사용하는 경우가 많아지다 보니, 어떤 Task에 사용하느냐에 따라 사용성이 결정되는 모델이 많기 때문에 이런 질문자체가 무의미한 경우도 많습니다.

  "Downstream Task"는 인공지능(AI)과 자연어 처리(NLP) 분야에서 자주 사용되는 용어로, 주로 사전훈련된 모델을 특정한 응용 분야에 맞게 적용하는 작업을 의미합니다. 이 개념은 자연어 처리 모델의 학습 과정에서, 기본적인 언어 이해를 위한 사전 훈련(Pre-training) 이후 이루어지는 별도의 작업을 설명합니다. 여기서의 "downstream"은 사전훈련된 모델이 처리해야 할 구체적인 응용 과제를 가리킵니다.
  
  

  • 다음은 Downstream Task의 일반적인 사례입니다.
    1. 텍스트 분류: 사전 훈련된 모델을 사용하여 문서를 카테고리나 주제별로 분류하는 작업입니다. 예로는 스팸 이메일 필터링, 뉴스 기사 분류 등이 있습니다.
    2. 감정 분석(Sentiment Analysis): 텍스트에서 감정이나 의견을 추론하는 작업입니다. 리뷰나 소셜 미디어 포스트에서 긍정, 부정, 중립 감정을 탐지하는 것과 같은 응용 분야가 있습니다.
    3. 질문 답변(Question Answering): 긴 문서나 단락에서 사용자의 질문에 대한 특정 답변을 추출하는 작업입니다. 이는 고객 서비스 봇이나 정보 검색 시스템에서 활용될 수 있습니다.
    4. 개체명 인식(Named Entity Recognition, NER): 텍스트에서 인물, 기관, 장소 이름과 같은 고유 명사를 식별하는 작업입니다. 이는 정보 추출과 데이터 정리에 사용됩니다.
    5. 번역(Machine Translation): 한 언어로 작성된 문장을 다른 언어로 번역하는 작업입니다.
  • Downstream Task를 수행할 때 사전 훈련된 모델, 예를 들어 BERT, GPT 등의 모델을 활용하여 특정한 과제를 위해 추가적인 학습을 시킵니다. 이는 주로 소량의 레이블이 된 데이터로 이루어지며, 모델이 이미 언어의 기초적인 패턴을 배우고 있기 때문에 빠르고 효율적으로 작업할 수 있도록 돕습니다. Downstream Task는 AI 모델의 실제 응용 가능성을 테스트하고 발전시키는 중요한 과정입니다.

  • ex) BERT를 이용하여 문장을 분류한다거나, Language Model의 특성을 이용하여 문장을 생성해내기도 합니다.

    • 물론 학습방식 때문에 문장 생성은 BERT보다는 GPT-3를 권하는 경우가 많습니다.

• 쉴새없이 나오는 모델들과 알고리즘을 따라가기 위해 쉼없이 공부하다 보니, 정작 분류모델과 생성모델은 근본적으로 무엇이고 어떤 차이가 있는 것인가?라는 기본적인 질문에 대한 대답을 못하고 있는 자신을 발견하게 되었습니다.

  • 생성모델이 무엇이냐는 질문을 받으면, 데이터를 생성해주는 모델! 이라는 정도의 대답을 못하였습니다.

  • 자료조사를 하면서 느꼈던 점은, 생성모델 자체를 정의하고 어떤 모델이 생성모델이다라고 정확히 분류한 자료는 많지 않다는 것입니다.

  • 그 이유는 생성모델 자체가 보통 데이터의 분포를 추정하는 모델이 대부분이다 보니 추정된 분포를 이용하여 다른 TASK에 사용되는 경우로 알려져 있는 경우가 많이 있기 때문입니다.

    • 예를 들어, 아래에서 설명할 Kernel Density Estimation은 데이터의 이상치를 찾는데 많이 활용되는 모델입니다. 하지만 이는 데이터 분포를 추정하여 데이터를 생성할 수 있는 생성모델이기도 합니다.

      • 즉, 이처럼 다른 Task로 알려져있는 경우도 많이 있어 자신이 생성모델을 활용하고 있으나 이를 모르는 경우도 많이 있습니다.

판별모델(Discriminative Model) vs 생성 모델(Generative Model)

• 판별모델(Discriminative Model)이란 데이터 X가 주어졌을때 Label Y가 나타날 조건부확률 P(Y|X)를 직접적으로 반환하는 모델입니다.

  • 분류모델이라고도 부릅니다.

  • 당연히 LABEL 정보가 있어야하기 때문에 지도학습 모델이라고 볼 수 있습니다.

• 생성모델(Generative Model)은 두가지로 나눌 수 있습니다.

  1. 지도적 생성모델

     • LABEL이 있는 데이터에 대해서 각 클래스 별 특징 데이터의 확률분포 P(X|Y)를 추정한 다음 베이즈 정리를 사용하여 P(Y|X)를 계산하는 방법입니다.
     • P(Y|X)를 계산할 수 있기 때문에 분류모델로 활용할 수도 있고 클래스별 Conditional 확률 P(X|Y)를 추정했기 때문에 확률분포 상에서의 새로운 가상의 데이터를 생성하거나 확률분포 끝자락에 있는 데이터를 이상치로도 판단하는 이상치 판별 모델로도 활용할 수 있습니다.

  2. 비지도적 생성모델

     • LABEL이 없어서, 데이터 X자체의 분포를 학습하여 X의 모분포를 추정하는 학습데이터의 분포를 학습하는 모델입니다.

     • 실제 대부분의 생성모델은 이 비지도적 생성모델이라고 생각하면 될 것 같습니다. GAN기반의 모델류들을 이용하여 새롭고 신기한 사진을 생성해내는 경우를 많이 보셨을텐데요. 원본이미지(X)의 확률분포를 학습하여 새로운 데이터를 생성해내는 비지도적 생성모델의 대표적인 예시입니다.

2. 생성모델의 종류

• 생성 모델은 우리가 데이터를 어떻게 레이블링하느냐에 따라 지도적 생성 모델과 비지도 생성 모델로 나눌 수 있습니다.

  • 각각의 모델은 학습 과정에서 레이블의 유무에 따라 다른 접근 방식을 취합니다.

• 구분점 및 응용

  • 레이블의 유무: 지도 생성 모델에서는 학습 시 레이블 정보가 필요하지만, 비지도 생성 모델에서는 레이블 없어도 됩니다.

  • 응용 분야

    • 지도적 방법은 특정 조건에 맞춘 데이터 생성(예: 특성 변환, 특정 조건 하 이미지 생성)에 사용

    • 비지도적 방법은 데이터 증강, 데이터 분포 이해, 잠재 공간 탐색 등에 활용

  • 각각의 방법은 사용자의 목적에 따라 적절하게 선택되며, 특히 생성적 적대 신경망(GAN)과 변이형 오토인코더(VAE) 같은 모델은 다양한 응용 분야에서 효과적으로 사용되고 있습니다.

지도적 생성 모델 (Supervised Generative Model)

• 지도적 생성 모델은 학습할 때 입력 데이터와 해당 레이블이 함께 제공되는 경우입니다. 이 모델의 목표는 주어진 입력에 대해 조건부 확률 분포를 학습하는 것입니다.

  • 조건부 확률 분포: $P(\text{label} \mid \text{data})$

    표현은 "데이터"가 주어졌을 때 "레이블"의 조건부 확률을 나타냅니다. 기계 학습과 통계의 맥락에서, 이는 종종 사후 확률로 불립니다. 이 확률은 관찰된 데이터를 고려했을 때 특정 레이블의 확률을 알려주며, 베이즈 추론에서 중심 개념입니다.

    • 이 확률을 이해하기 위한 더 많은 배경은 다음과 같습니다

    1. 베이즈 추론: 베이즈 통계에서 우리는 더 많은 증거("데이터")가 주어질 때 가설(이 경우 "레이블")의 확률에 대한 믿음을 업데이트합니다. 사후 확률은 베이즈 정리를 사용하여 계산합니다.
       $P(\text{label} \mid \text{data}) = \frac{P(\text{data} \mid \text{label}) \cdot P(\text{label})}{P(\text{data})}$

    • Where
      • $P(\text{data} \mid \text{label})$ 은 가능도(likelihood)로, 레이블이 주어졌을 때 데이터를 관찰할 확률입니다.
      • $P(\text{label})$은 사전 확률(prior probability)로, 데이터를 관찰하기 전에 레이블에 대해 알고 있는 바를 나타냅니다.
      • $P(\text{data})$은 주변 가능도(marginal likelihood) 또는 증거(evidence)로, 모든 가능한 레이블 하에서 데이터를 관찰할 총 확률입니다.

    2. 기계 학습에서의 응용: 이 확률은 특정 데이터 인스턴스에 대해 가장 가능성 있는 클래스(또는 레이블)를 결정하고자 할 때 분류 문제에 자주 사용됩니다. 나이브 베이즈 분류기와 같은 알고리즘은 이러한 확률을 명시적으로 계산하여 예측을 수행합니다.
    3. 해석: 데이터에 조건화된 레이블을 이해하는 것은 모델 출력에 기반한 정보에 입각한 결정을 내리는 데 도움을 줍니다. 높은 사후 확률은 주어진 데이터에 특정 레이블에 대한 강한 증거를 나타냅니다.

• 주요 특징

  • 데이터 라벨링: 모델은 각 데이터 포인트에 대한 레이블 정보가 주어진 상태로 학습됩니다.

  • 목적: 주어진 입력 데이터에 따라 올바른 출력을 생성하는 능력을 학습합니다. 이는 일반적으로 분류나 회귀 작업에 응용될 수 있습니다.

  • 예시: 조건부 GAN (Conditional GAN, cGAN)은 특정 레이블을 조건으로 하여 새로운 데이터를 생성하는 대표적인 지도적 생성 모델입니다. 예를 들어, 숫자 "3"이라는 레이블이 주어질 때 해당 숫자를 나타내는 이미지를 생성할 수 있습니다.

비지도 생성 모델 (Unsupervised Generative Model)

• 비지도 생성 모델은 데이터에 대한 레이블이 주어지지 않은 상태에서 학습하는 경우입니다. 이 모델은 입력 데이터의 확률 분포를 학습하여 새로운 데이터를 생성합니다.

  • 확률 분포: $P(\text{data})$

    $P(\text{data})$는 "데이터"의 확률을 나타내며, 통계와 기계 학습에서 중요한 개념입니다. 이 확률은 데이터를 관찰할 전체 확률 또는 주변 확률(marginal likelihood)로 불리며, 종종 베이즈 정리에서 분모 역할을 합니다.

    1. 맥락에서의 역할
       • 베이즈 추론에서, $P(\text{data})$는 모든 가능한 레이블에 대해 데이터를 관찰할 수 있는 총 확률을 의미합니다.
         • 이는 모델의 출력을 확률 형태로 해석할 때 필요합니다.
       • 이 값은 사후 확률 계산에서 정규화 상수로 작용하여, 다른 조건부 확률 계산의 기준이 됩니다.
    2. 계산 방법
       • $P(\text{data})$는 보통 다음과 같이 계산됩니다.
         • $P(\text{data}) = \sum_{\text{labels}} P(\text{data} \mid \text{label}) \cdot P(\text{label})$
         • 여기서 모든 가능한 레이블에 걸쳐서 각 레이블에 대한 가능도와 사전 확률의 곱을 더합니다.
    3. 중요성
       • $P(\text{data})$를 정확하게 계산하는 것은 종종 어려울 수 있습니다, 특히 데이터 차원이 크거나 복잡한 경우. 이 때문에, 많은 경우에는 근사 기법이나 샘플링 기법을 사용합니다.
         이 개념은 특히 기계 학습의 베이즈 모델링에서 유용하며, 모델이 새로운 데이터를 어떻게 이해하고 처리할지를 결정하는 데 도움을 줍니다.

• 주요 특징

  • 데이터 라벨링 불필요: 모델은 레이블 없이 순수 데이터만을 통해 학습합니다.

  • 목적: 데이터의 숨겨진 구조를 이해하고 새로운 샘플을 생성하는 데 중점을 둡니다.

  • 예시: 기본적인 GAN이나 VAE는 데이터의 전반적인 생성 메커니즘을 학습하여, 임의의 입력으로부터 새로운 데이터를 생성하는 비지도 학습 방식의 대표적인 예입니다.

3. 지도형 생성 모델의 종류

선형 판별 분석 (Linear Discriminant Analysis, LDA)

• LDA는 두 개 이상의 클래스가 있는 데이터셋에서 클래스 간의 차이를 최대화하고, 클래스 내의 차이는 최소화하는 선형 결정 경계를 찾습니다.

• 특징

  • 가정: 각 클래스는 동일한 공분산 행렬을 갖는 다변량 가우시안 분포를 따릅니다.

  • 목표: 데이터의 투영을 통해 클래스 분리를 최적화하는 방향 벡터를 찾습니다. 이를 통해 고차원의 데이터를 저차원으로 투영하면서도 최대한의 분리성을 유지합니다.

  • 적용: 이 알고리즘은 특히 차원이 높은 데이터셋에서 주요한 차원을 식별하고, 컴퓨터 비전 및 패턴 인식에서 사용됩니다.

  • 장점: 계산이 빠르고 선형성을 가정하여 과적합을 줄이는 데 유리합니다.

이차 판별 분석 (Quadratic Discriminant Analysis, QDA)

• QDA는 LDA와 유사하지만, 각 클래스가 서로 다른 공분산 행렬을 가질 수 있다고 가정하여, 더 복잡한 결정 경계를 만들 수 있습니다.

• 특징

  • 가정: 각 클래스는 고유한 공분산 행렬을 갖는 다변량 가우시안 분포를 따릅니다.

  • 목표: 각 클래스에 적합한 이차 결정 경계를 학습하여 데이터를 분류합니다.

  • 적용: 클래스들이 선형적으로 분리가 어렵고 공분산이 다른 경우에 유용합니다.

  • 단점: 클래스 수가 많거나 데이터가 적은 경우 과적합 위험이 있고, 계산 비용이 LDA보다 큽니다.

비교 및 선택

• LDA는 더 단순하며 일반적으로 계산이 빠르지만, 모든 클래스가 동일한 공분산을 갖는다는 제한된 가정이 있습니다.

  • 데이터가 이러한 가정에 적합하다면 효과적일 수 있습니다.

• QDA는 더 유연하며 클래스 간의 공분산이 다를 수 있는 환경에서 효과적이지만, 더 많은 파라미터를 추정해야 하기 때문에 데이터가 충분히 많지 않으면 과적합될 위험이 있습니다.

• 결론적으로, LDA와 QDA는 데이터의 분포와 문제의 특성에 따라 선택해야 합니다.

  • 데이터가 선형적으로 잘 분리되지 않거나 클래스 간의 공분산 차이가 큰 경우에는 QDA가 나은 선택일 수 있습니다.

4. 비지도형 생성 모델의 종류

• 이 두 가지 접근법은 서로 다른 장단점과 응용 분야를 가지고 있어, 사용자의 문제에 따라 적절한 모델을 설계해야 합니다.

  • 통계적 모델은 더 간단하고 해석이 가능하지만 복잡한 데이터 구조를 처리하는 데 한계가 있을 수 있으며, 딥러닝 모델은 복잡하고 고차원적인 데이터 생성에 강력함을 보입니다.

통계적 생성 모델

• 통계적 생성 모델이란 밀도 추정을 의미한다고 생각하면 좋을것 같습니다.

  • 관측된 데이터들의 분포로부터 원래 변수의 확률분포를 추정하고자 하는 것이 밀도 추정입니다.

  • 사실상 통계 책에 나오는 모수적/비모수적 추정과 같죠.

    모수적 추정과 비모수적 추정은 통계학에서 데이터의 분포를 추정하는 두 가지 접근 방식입니다. 각 방식은 데이터의 성격과 분석 목적에 따라 선택될 수 있습니다.

    1. 모수적 추정 (Parametric Estimation)
       • 모수적 추정은 데이터가 특정한 분포(예: 정규분포, 이항분포 등)를 따른다고 가정하고, 이 분포를 설명하는 모수를 추정하는 방법입니다.
         • 예를 들어, 정규분포의 경우 평균(μ)과 표준편차(σ)가 모수가 됩니다.
       • 모수적 방법은 일반적으로 계산이 단순하고, 적절한 분포 가정이 이루어졌다면 효율적입니다.
         • 다만, 잘못된 분포 가정을 할 경우 부정확한 결과를 초래할 수 있는 단점이 있습니다.
    2. 비모수적 추정 (Non-parametric Estimation)
       • 비모수적 추정은 특정한 분포 가정을 하지 않고, 데이터 자체로부터 분포를 추정하는 방법입니다.
         • 이러한 방법은 데이터의 분포에 대한 사전 가정이 없어 유연한 분석이 가능하며, 특히 잘 알려지지 않거나 분포를 가정하기 어려운 경우에 유용합니다.
       • 예로는 커널 밀도 추정이나 히스토그램 같은 방법이 있습니다.
       • 비모수적 방법은 일반적으로 모수적 방법에 비해 계산이 더 복잡하고, 큰 데이터 세트가 필요할 수 있다는 점이 한계일 수 있습니다.

• 대표적인 예시로 커널 밀도 추정(Kernel Density Estimation)이 있습니다.

  • 랜덤변수 X에 대한 PDF를 다음과 같이 추정하는 것입니다.

  • 어떤 커널 모양이냐에 따라 PDF가 달라지겠죠?

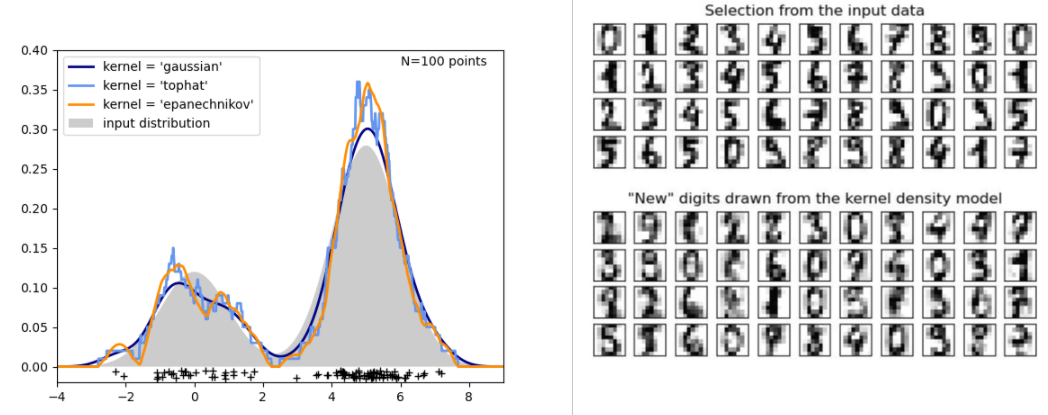
• 아래 왼쪽 그래프를 보시면, 검은색 선이 원 데이터를 나타내고 , 이에 걸맞는 분포를 Kernel값을 통해 추정하는 겁니다.

  • 여기서 커널은 ‘가우시안’, ‘TOPHAT’, ‘EPANECHNIKOV’를 사용했는데요, 원 데이터의 분포를 잘 추정하고 있음을 확인할 수 있습니다.

  • 이처럼 원 데이터의 분포를 추정하는 생성모델을 Kernel Density Estimation이라고 합니다.

  • 원 데이터의 분포를 추정했기 때문에 추정한 분포로부터 새로운 데이터를 생성할 수 있겠죠?

• 오른쪽 MNIST(Modified National Institute of Standards and Technology database) 사진을 보시면 MNIST 픽셀들의 분포를 학습하여, KDE(Kernel Density Estimation)로 새로운 숫자이미지를 생성한 것입니다.

• 통계적 생성모델은 가우시안 밀도 추정/혼합 가우시안 밀도 추정 모델입니다.

  • 원래의 분포가 정규분포를 따른다고 가정하는 것입니다.

• 혼합가우시안 밀도 추정 모델은 여러 가우시안 분포의 합으로 이루어져있다고 가정하는 것이죠.

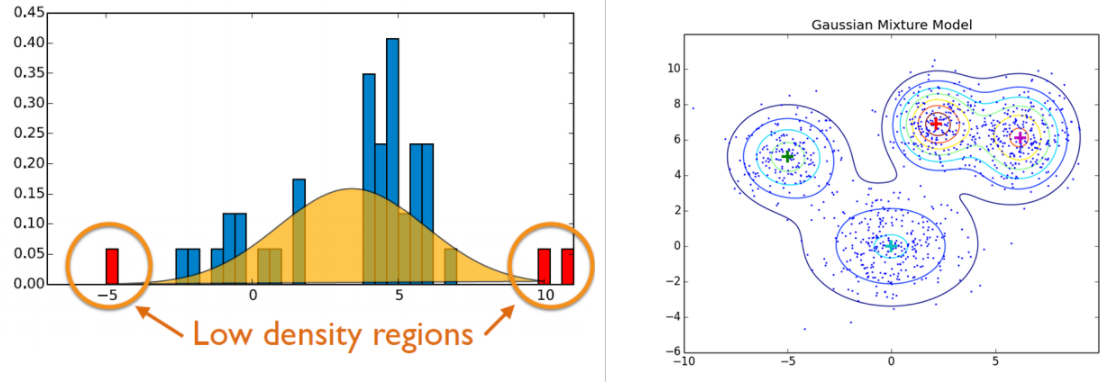
  • 왼쪽 아래 그림을 보시면 파란색 데이터 분포를 정규분포로 가정하고, 각각의 끝자락에 있는 부분들을 이상치로 판단하죠.

  • 이렇게 원 데이터의 분포를 학습해 이상치 탐지 모델로도 쓰입니다. 혼합가우시안 모델 같은 경우는 군집화 방법으로도 활용이 됩니다.

  • 우리가 많이 사용하는 k-means 같은 경우는 하나의 데이터는 하나의 군집에만 속할 수 있지만, GMM(Gaussian Mixture Model)같은 경우에는 한데이터가 여러군집에 속할 수 있으며, 각각의 군집에 속할 확률을 나타냅니다.

  GMM에서 쓰이는 EM알고리즘은 너무 복잡해서 여기서는 생략

1. 가우시안 혼합 모델 (Gaussian Mixture Model, GMM)

   • GMM은 데이터가 여러 개의 가우시안 분포의 혼합으로부터 생성된다고 가정하는 모델입니다.

   • 각 데이터 포인트가 특정 가우시안 분포에 속할 확률을 추정하며, EM(Expectation-Maximization) 알고리즘을 통해 추정 과정을 반복하여 모델을 학습합니다.

   • 데이터 클러스터링 및 밀도 추정에 유용하게 사용됩니다.

2. 잠재 디리클레 할당 (Latent Dirichlet Allocation, LDA)

   • LDA는 주로 문서 주제 모델링에 사용되는 기법입니다.

   • 문서가 여러 주제의 혼합으로 구성되어 있다고 가정하고, 각 문서에서 각 단어가 생성될 주제의 분포를 추정합니다.

3. 핵심 요소 분석 (Principal Component Analysis, PCA)

   • PCA는 데이터의 변동성을 최대화하는 방향으로 데이터를 투영하여 데이터의 주성분을 찾는 방법입니다.

   • 데이터의 차원을 축소하고, 숨겨진 구조를 파악하는 데 사용됩니다.

딥러닝 기반 생성 모델

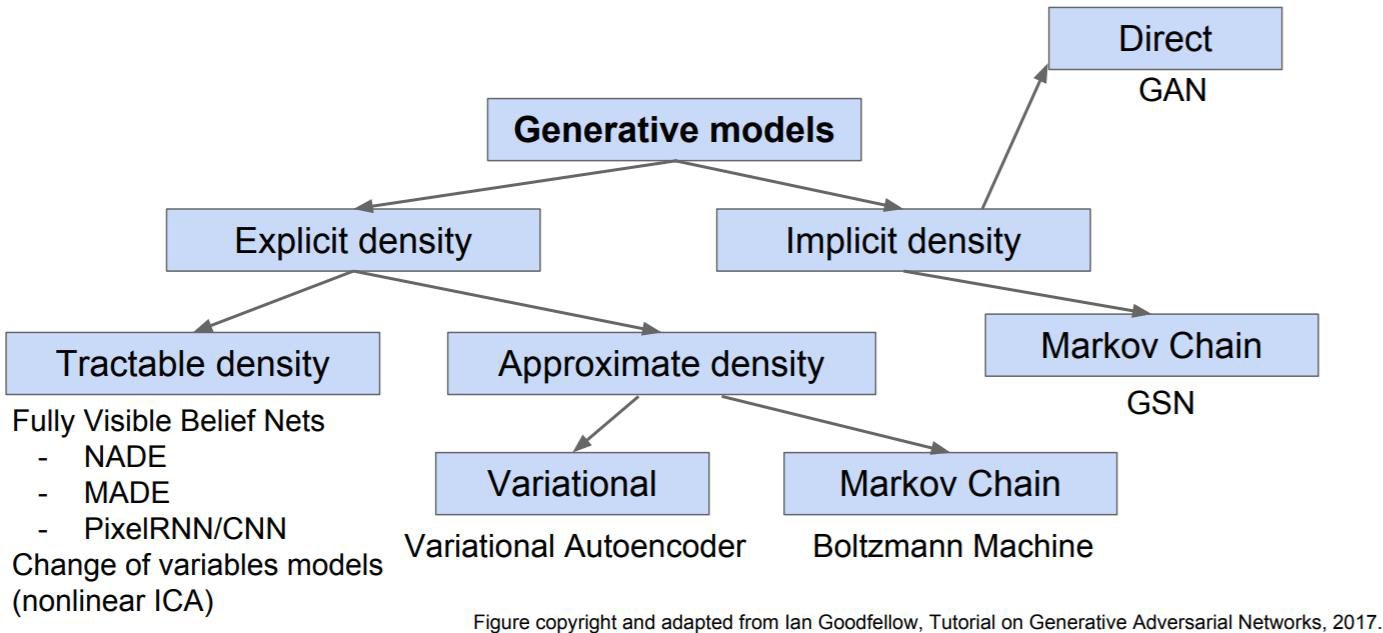
• Ian Goodfellows는생성모델을 세분화해서 크게 3가지로 나누었다.

  • 위의 통계적 생성모델처럼 확률분포를 추정하는 건 똑같으나, 어떤 방식으로 추정할지에 따라서 구분

  

  1. Tractable Density: 데이터 X를 보고 확률분포를 ‘직접’ 구하는 방법

  2. Approximate Density: 데이터 X를 보고 확률분포를 ‘추정’하는 방법

  3. Implicit Density: 데이터 X의 분포를 몰라도 되는 방법

1. Approximate Density: 변이형 오토인코더 (Variational Autoencoder, VAE)

   • VAE는 오토인코더 구조를 기반으로 하되, 데이터의 잠재 공간을 확률 분포로 모델링합니다.

   • 각 데이터 포인트는 잠재 공간에서 정규 분포의 평균과 분산을 통해 샘플링되며, 샘플링된 벡터에서 데이터를 재구성하는 데 사용됩니다.

     • 이는 생성적 특성을 부여합니다.

   • VAE는 연속적인 데이터 생성 및 데이터의 부드러운 변형에 적합합니다.

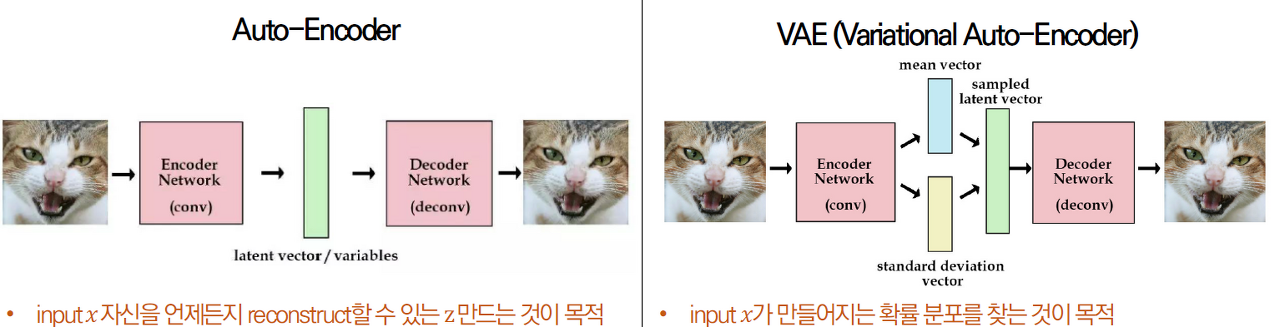
   • 원 데이터의 Feature를 압축해서 복원하는 Encoder-Decoder 관게를 이용하죠.

     • 하지만 VAE의 경우는 Auto-Encoder와는 살짝 차이가 있습니다.

     • latent vector에 정규분포 항을 추가하여, latent vector를 조금씩 변형하면서 복원하는게 그 목적이죠.

       • 다양한 종류의 데이터를 생성해낼 수 있다.

   • VAE는 학습시 두가지 에러를 사용합니다.

     1. Reconstruction Loss

        • 직관적으로는 생성모델이 만든 새로운 데이터와 원래 데이터와의 관계를 살펴보는 것이 Reconstrucion Loss 입니다.

     2. Regularization Loss

        • 데이터가 원래 가지는 분포와 동일한 분포를 가지게 학습하기 위해 True 분포를 추정한 함수의 분포에 대한 loss term이 Regularization loss입니다.

   • VAE는 원 데이터의 분포를 추정하고 이를 맞추려고 하면서 학습되는 방법을 사용합니다.

2. Implicit Density: 생성적 적대 신경망 (Generative Adversarial Network, GAN)

   • GAN은 두 개의 신경망으로 구성됩니다.

     1. 생성자(Generator)

        • 생성자는 임의의 노이즈로부터 현실적인 데이터를 생성

     2. 판별자(Discriminator)

        • 판별자는 입력된 데이터가 실제 데이터인지 생성된 것인지를 판단합니다.

   • 두 네트워크는 적대적으로 경쟁하며 발전하여, 생성자는 판별자를 속일 수 있을 정도로 현실적인 데이터를 생성할 수 있게 됩니다.

     • 위에서 Implicit Density의 경우 데이터 X의 분포를 ‘몰라도’ 된다고 했습니다.

     • 이는 GAN의 특이한 점 때문인데요. 바로 판별기, 생성기가 서로 경쟁하면서 학습이 되고, 학습과정을 자세하게 들여다보면 생성기에는 실제 데이터가 들어가지도 않습니다.

     • 오직 판별기가 차이를 구분해주죠. 그렇기에 생성기는 데이터 X를 쳐다본적도 없게 된 겁니다.

     • 이런 특성으로 인해 실제 데이터를 쳐다보지 않는다고 표현한 것입니다.

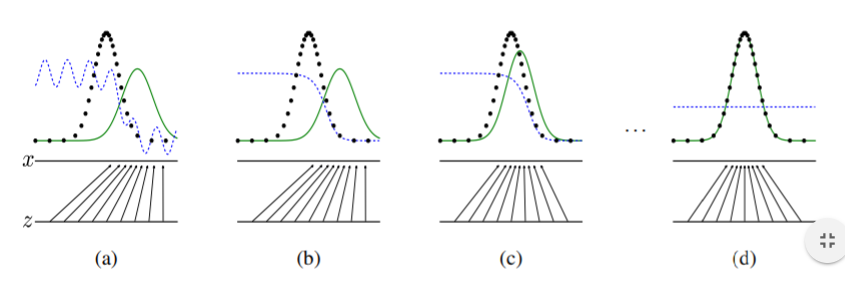
   • 아래 사진처럼, 원 데이터 분포와의 차이를 줄여나가는 방향으로 판별기와 생성기가 경쟁학습을 해서 원 데이터의 분포를 찾게 되는 것이죠.

   • GAN은 이미지 생성, 품질 향상, 스타일 전이 등 다양한 분야에 사용됩니다.

3. 자기회귀 모델 (Autoregressive Model)

   • 데이터 포인트를 순차적으로 생성하는 방식입니다.

   • 예로는 PixelRNN, PixelCNN, WaveNet 등이 있으며, 모든 이전 데이터를 기반으로 새로운 데이터를 생성합니다.

     • Tractable Density : Pixel RNN

       • 이전 픽셀이 어떤 것인지에 따라 다음 픽셀이 무엇이 나오는지를 순서대로 확인(학습)하는 모델입니다.

       • Chain Rule을 통해서 직접적으로 학습데이터의 분포를 구하는 것이라고 볼 수 있죠.

       • 이렇게 해서 이미지 전체에 대한 확률분포를 직접적으로 구하는 모델을 만드는 것이죠.

       • 이처럼 이전 픽셀의 정보를 가지고 있어야 다음 픽셀의 분포를 알 수 있기에, 직접적으로 확률분포를 구하는 방법이라고 볼 수 있습니다.