[백준] #2775 부녀회장이 될테야(python)

수영·2022년 8월 7일

DP Python3 백준

백준

목록 보기

25/117

📌문제

평소 반상회에 참석하는 것을 좋아하는 주희는 이번 기회에 부녀회장이 되고 싶어 각 층의 사람들을 불러 모아 반상회를 주최하려고 한다.

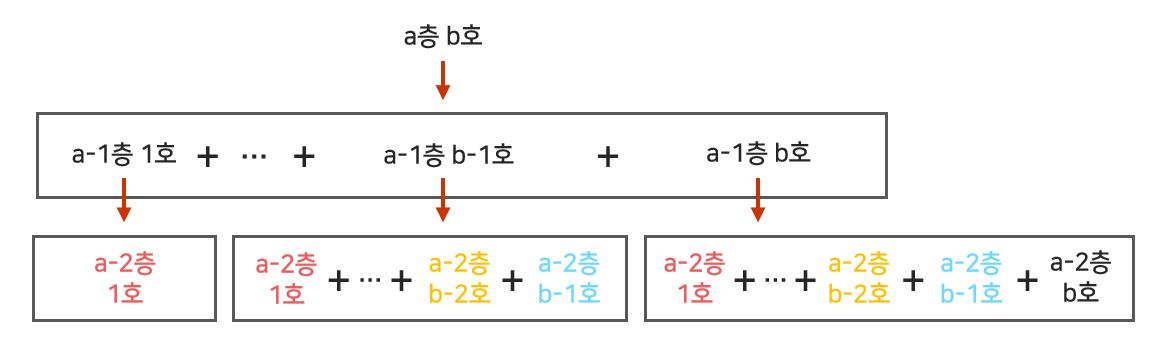
이 아파트에 거주를 하려면 조건이 있는데, “a층의 b호에 살려면 자신의 아래(a-1)층의 1호부터 b호까지 사람들의 수의 합만큼 사람들을 데려와 살아야 한다” 는 계약 조항을 꼭 지키고 들어와야 한다.

아파트에 비어있는 집은 없고 모든 거주민들이 이 계약 조건을 지키고 왔다고 가정했을 때, 주어지는 양의 정수 k와 n에 대해 k층에 n호에는 몇 명이 살고 있는지 출력하라. 단, 아파트에는 0층부터 있고 각층에는 1호부터 있으며, 0층의 i호에는 i명이 산다.

입력

첫 번째 줄에 Test case의 수 T가 주어진다. 그리고 각각의 케이스마다 입력으로 첫 번째 줄에 정수 k, 두 번째 줄에 정수 n이 주어진다

출력

각각의 Test case에 대해서 해당 집에 거주민 수를 출력하라.

제한

1 ≤ k, n ≤ 14

예제 입력

예제 출력

6
10

백준 2775번 문제

💡Idea

문제를 보자마자 "이거 DP로 풀면 되겠다😲"는 생각이 들었습니다.

a층의 b호에 살고 있는 사람들을 알기 위해서는 a-1층의 1호부터 b호까지의 거주민의 수를 알아야 하고, 또 다시 a-1층의 각 거주민의 수를 알기 위해서는 a-2층의 거주민의 수를 활용해야 합니다.

위와 같이 문제를 해결하는 과정에서 중복되는 부분 문제들이 있기 때문에, DP로 푸는 것이 좋습니다.

동적계획법(DP, Dynamic Programming)에 대해 알고 싶다면?

👇 점화식은 아래와 같이 세울 수 있었습니다.

$P_{a,b} = \displaystyle\sum_{n = 1}^{b}P_{a-1, n}$
$P_{0, i} = i$

💻코드

import sys
input = sys.stdin.readline

T = int(input())

for _ in range(T):
    k, n = int(input()), int(input())
    dp = [[0 for _ in range(n + 1)] for _ in range(k + 1)]
    dp[0] = [x for x in range(n + 1)]
    for i in range(1, k + 1):
        for j in range(1, n + 1):
            dp[i][j] = sum(dp[i - 1][:j + 1])

    print(dp[k][n])