PCA(Principal Component Analysis)
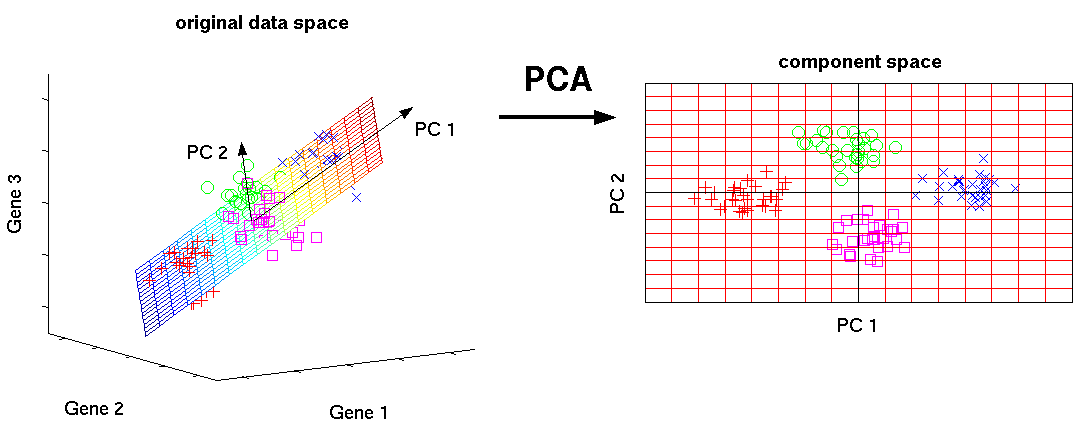
[https://pt.slideshare.net/hihijungho/pca-principal-component-analysis]
1. 모델이 사용되는 문제(도메인)
Clustering, Dimensionality Reduction, Visualization, Noise Reduction
label이 없는 상태에서 데이터의 경향성을 분석하거나 데이터 간 Colinearity를 제거하는 데에 이용됩니다.
2. 모델의 구조 및 학습 방법
모델에서 가장 큰 분산값을 가지게 하는 방향벡터(Pricinpal Component)를 찾는 알고리즘입니다. 이를 orthogonal basis(기저 벡터) 라고 하는데, 이는 새로운 직교좌표계의 역할을 하게 됩니다. 이를 기반으로 고차원으로부터 저차원으로의 projection(사영)을 진행합니다. 이를 통해 이차원(또는 축소된 m 차원)으로 시각화된 데이터 분포를 관측 가능합니다. 이러한 과정으로 variance를 유지(정보 손실을 막으며) 차원을 축소하게 됩니다.
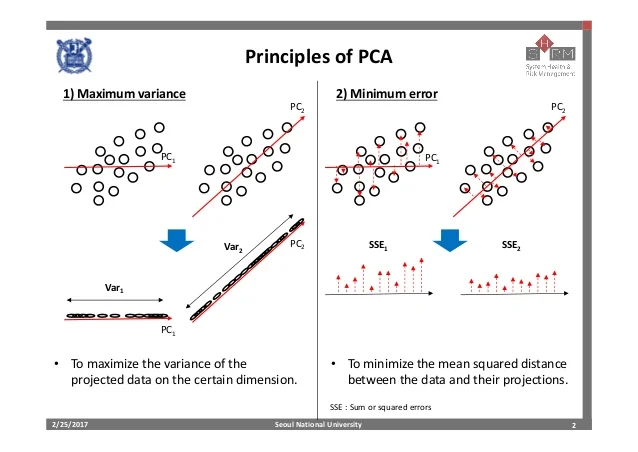
[https://pt.slideshare.net/hihijungho/pca-principal-component-analysis]
학습 방법
- d-dimensional data 대해 각 차원의 평균에 대해 뺄셈을 하여 평균이 0이 되도록 합니다.
- 위 데이터들의 편차에 대한 Covariance matrix()를 계산합니다. 이 Covariance matrix는 dimension 안에 각 feature상관관계를 나타냅니다.
- 공분산 행렬에대한 eigenvalue 디컴퍼지션을 하여 Eigenvalue 와 Eigenvector를 구합니다. 이 때, eigenvector는 행렬이 벡터의 변화에 작용하는 basis의 방향을 나타내며, eigenvalue는 basis 방향으로 얼마만큼 늘려지는지 그 크기를 의미합니다.
- 전체데이터를 그 Eigenvector에 정사영 시켜서 데이터들의 패턴을 파악합니다.
3. 모델의 시간 복잡도
Covariance Matrix : (개의 data에 대한 covariance matrix )
eigen-value decomposition : ( 벡터에 대한 개의 eigenvector)
4. 다른 방법들 대비 장단점
장점
- 데이터 고유의 물리량을 보존하면서 차원축소를 하기 때문에, 차원의 저주에 빠진 데이터에 적용하면 유의미한 효과를 볼 수 있습니다.
- feature 수가 줄어들어 연산 속도가 빨라지게 합니다.
단점
- basis 가 가지는 의미를 설명하기 어렵습니다.
- 분산을 최대로 한다고 해서 feature의 구분을 좋게 하는 것은 아닙니다.
