Span / Basis / Rank / Linear Projection

Span

주어진 벡터들의 조합(합, 차 등)으로 만들 수 있는 가능한 모든 벡터의 집합. 즉, 공간입니다.사용하는 벡터에 따라 모든 공간을 채울 수도, 부분적인 공간만 채울 수도 있습니다.

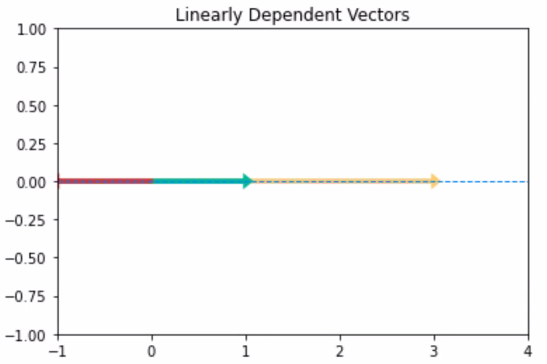
선형 관계의 벡터(즉, 선형종속)은 조합을 통해 선 외부의 새로운 벡터를 생성할 수 없습니다.2차원 평면 상에 존재는 하지만, span은 벡터가 올려져 있는 선으로 제한하는 것입니다.

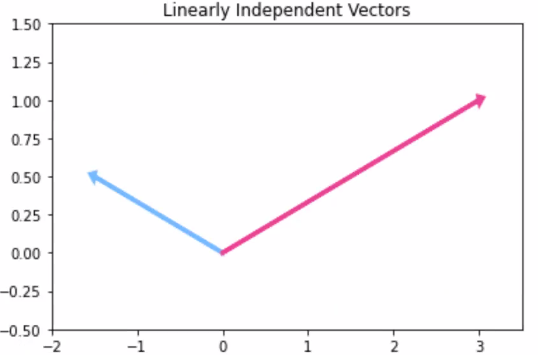
반면에 선형 관계가 없는 벡터(즉, 선형독립)은 주어진 공간의 모든 벡터를 조합을 통해 만들 수 있습니다.아래 그림처럼 (0, 0)에 시작을 고정시킨 상태로 두 벡터의 조합을 통한 벡터 생성을 떠올려 보면 됩니다.

벡터공간 $V$에 대하여 집합 $S$를 $S = \{ v_i |v_i \in V , i \in I \}$ 라 하자. 이 때 span은 다음과 같이 정의합니다!

• $span(S)$ : $S$에 속하는 벡터들의 선형 결합으로 나타날 수 있는 모든 벡터의 집합. 이 때 $span(S)$는 $V$의 $subspace$로서 벡터공간이 됩니다.

  ex) $span(\{ \left[ \begin{matrix} 0 \\ 1 \\ \end{matrix} \right] , \left[ \begin{matrix} 1 \\ 1 \\ \end{matrix} \right] \}) = \R^2$, $span(\{ \left[ \begin{matrix} 0 \\ 1 \\ \end{matrix} \right] \}) = \{(0, y)| y \in \R \}$

• $span(S)$에 대하여 $S$를 $span(S)$의 spanning set, 혹은 generating set이라고 하며, $span(S)$를 $S$의 linear span, 혹은 span이라고 한다.
• $span(S) = V$일 때, $S$의 원소의 갯수는 $V$에 속하는 선형 독립적인 벡터들의 집합의 원소의 갯수보다 같거나 크다.

---

Basis

Basis는 공간을 이룰 수 있는 선형 독립 상태인 벡터들의 모음인데, span의 역개념입니다.

벡터공간 $V$에 대하여 기저집합 $B$ 는 다음과 같이 정의됩니다.

• $V$에 속하는 모든 벡터가 $B$에 속하는 벡터들의 유일한 선형 결합으로 표현 가능합니다.

• 혹은, 다음과 같이 정의할 수도 있습니다.

  • $B$는 선형 독립입니다.
  • $span(B) = V$입니다.

• 두 정의는 서로 필요충분조건이 되며, 하나를 정의로 사용할 경우 다른 하나가 basis의 성질이 됩니다.

  ex) $\R^3$의 basis $\{ \left[ \begin{matrix} 0 \\ 1 \\ 0 \\ \end{matrix} \right] , \left[ \begin{matrix} 1 \\ 1 \\ 0 \\ \end{matrix} \right], \left[ \begin{matrix} 0 \\ 0 \\ 1 \\ \end{matrix} \right] \}$

• 위 span의 성질과 조합해 보면, 다음 네 명제가 모두 동치임을 알 수 있습니다.

  • $B$는 $V$의 basis입니다.
  • $B$는 $V$의 가장 작은 generating set입니다.
  • $B$는 $V$의 선형 독립인 부분집합 중 가장 크기가 큽니다.
  • $V$의 벡터들은 모두 $B$의 선형 결합으로 유일하게 표현 가능합니다.

• orthogonal basis : n차원 실수공간 $\R^{n}$에서 orthogonal basis란 $\R^{n}$의 basis들 중 모든 벡터가 서로 직교하는 basis를 말한다. 이 때 각 벡터의 크기가 1로 normalize되어있을 경우, 이를 orthonormal basis라 합니다.

  ---

Rank(계수)

매트릭스의 Rank란 매트릭스의 열을 이루고 있는 벡터들로 만들 수 있는 공간(span)의 차원입니다.

매트릭스의 벡터들 가운데 서로 선형 관계가 있을 수 있기 때문에 매트릭스의 차원과는 다를 수 있습니다.예를 들어 3차원 행렬에서 rank 값이 3이 출력될 것이라고 생각 했는데 2가 출력됐다고 한다면, 3개의 벡터 중 2개는 선형 종속 관계를 가진다는 거다.또, 20*55 shape의 데이터를 가지고 상관 관계를 나타내고자 할 때, Rank 값이 15라고 한다면 전체 데이터를 다 신경 쓸 필요가 없다는 의미입니다.

즉, Rank 값을 확인하면 매트릭스가 이루고 있는 벡터들의 선형 관계가 있는지 확인할 수 있습니다.

행렬 $A$에 대해서 rank는 다음과 같이 정의됩니다.

• $rank(A)$ : $A$의 열공간에 대한 차원. 즉 $A$의 열벡터들을 선형 결합하여 나오는 벡터공간($C(A)$)에서 선형 독립인 벡터의 최대 갯수를 의미합니다. column rank와 같은 의미입니다.

  ex) $A = \left[ \begin{matrix} 1 & 2 \\ 3 & 4 \\ \end{matrix} \right]$ 인 경우 $rank(A) = 2$ , $A = \left[ \begin{matrix} 1 & 2 & 2\\ 3 & 4 & 6\\ \end{matrix} \right]$ 인 경우 $rank(A) = 2$

• row rank : $A$의 행공간에 대한 차원
• full rank : $A \in \R^{m \times n}$에 대하여 $rank(A)=min(m,n)$일 때, 즉 $A$의 rank가 $\R^{m \times n}$에 속하는 행렬의 rank 중 가능한 가장 큰 값일 때 $A$는 full rank를 가졌다고 한다. 만약 $A$가 full rank를 가지지 않은 경우, $A$는 rank-deficient하다고 한다. 특히, $A \in \R^{n \times n}$인 정사각행렬일 경우 $A$가 역행렬을 가지기 위해서는 $A$는 반드시 full rank를 가져야만 합니다.
• $rank(A) = rank(A^\intercal) = rank(A^\intercal A) = rank(AA^\intercal)$

📖 Python

# 두 벡터 a=[12, 3], b=[5, 7]의 Rank 확인
df = pd.DataFrame({'a' : [12, 3], 'b' : [5, 7]})

np.linalg.matrix_rank(df)

정리span = 하나 이상의 벡터로 만들 수 있는 공간(n차원의 공간)rank = span의 차원의 수(n차원의 공간에서의 n)

---

Linear Projection (선형 투영)

Projection이란 한 벡터를 다른 벡터의 공간에 표기하는 것이라고 생각할 수 있습니다.

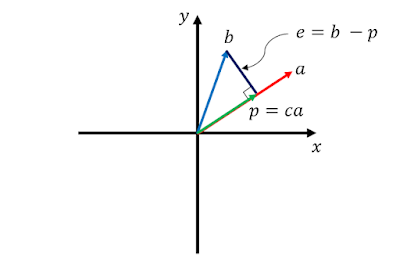
아래 그림에서 vector b를 vector a 위의 vector p 로 projection 한 것이다.vector a가 선(1차원) 위에 있는 경우, vector p는 아무리 스케일을 변화시켜도 결국 선 위에 있게 됩니다.

e = b-p 에서 e는 Error이다. 바로 e를 통해서 직교성을 알 수 있습니다.

🎈 원래라면 a와 b 두 벡터를 표현하기 위해서는 하나의 면이 필요하다. 그러나 정사영 시킨 후에는 하나의 선으로 벡터를 나타낼 수 있게 된다.만약 많은 feature를 가진 수많은 벡터가 있는 데이터를 가지고 있다고 해보자. 이 벡터들을 가능한 한 정사영 시켜 최소의 벡터로 표현할 수 있다면, 벡터들을 표현할 수 있는 차원을 축소시켜 저장공간, 즉 메모리를 최소화 할 수 있다는 뜻이 된다. 또한 알고리즘의 cost가 낮아지게 된다.

이것은 여러개의 feature 중에서 의미가 없거나 작은 것들은 제거하면서 원래 데이터가 제공하고자 하는 인사이트는 충분히 살릴 수 있는 차원 축소의 근본이 되는 기술이라고 할 수 있다.빅데이터에서 이를 활용한다면, 물리적 메모리, 딥러닝을 적용하기 위한 컴퓨터 파워 등이 절약되는 장점이 있다. 또한, 데이터 loss가 있음에도 불구하고 충분히 유의미한 결론을 도출할 수 있다는 데에 의미가 있다.