공분산(covariance) / 공분산 행렬(covariance matrix) / 상관계수(Correlation coefficient)

공분산(**covariance)**

• 두 변수에 대하여 한 변수가 변화할 때 다른 변수가 어떠한 연관성을 갖고 변하는지를 나타낸 값입니다.
• 두 변수의 연관성이 클수록 공분산 값도 커집니다.

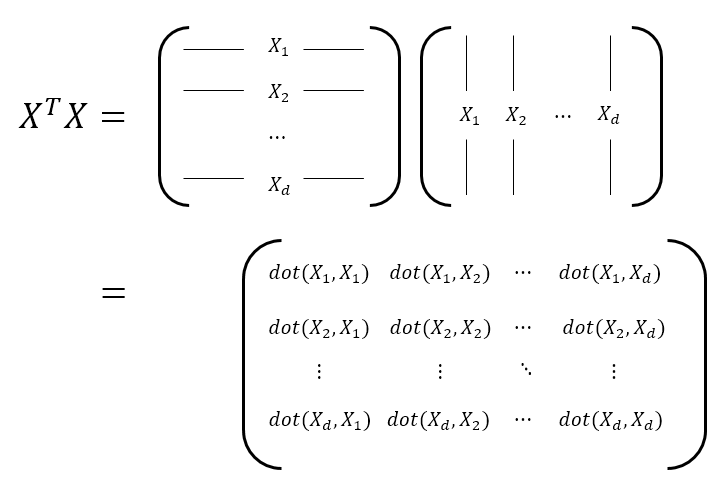
공분산 행렬(**covariance matrix)**

기하학적 의미
행렬 = 선형변환, 벡터 공간을 다른 벡터 공간으로 mapping

데이터 구조적 의미
각 feature의 변동이 얼마나 닮았는지 비교 ⇒ 분산 계산
개수의 크기가 커지면 값이 커지므로 이를 방지하기 위해 n으로 나눕니다.

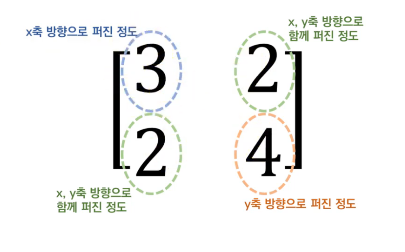
• 모든 변수에 대하여 분산과 공분산 값을 나타내는 정사각 행렬입니다.
  • 주 대각선 성분은 자기 자신의 분산 값을 나타냅니다.
  • 주 대각선 이외의 성분은 가능한 두 변수의 공분산 값을 나타냅니다.
• [df.cov()] 또는 [np.cov()]를 사용하여 구할 수 있습니다.

**상관계수(Correlation coefficient)**

• 공분산을 두 변수의 표준편차로 나눠준 값입니다.

  $r_{x, y} = \frac{cov(X,Y)}{\sigma_{X}\sigma_{Y}}$

• 공분산의 스케일을 조정하는 효과가 있습니다.
• 변수의 스케일에 영향을 받지 않습니다.
• 1에서 1 사이의 값을 가집니다. 상관계수가 1이라는 것은 한 변수가 다른 변수에 대해서 완벽한 양의 선형 관계를 갖고 있다는 것을 의미합니다.
  

• 패턴을 갖는 경우 상관계수가 0일수 있으므로 두 변수가 연관성이 없다라고 말 할 수는 없습니다.
• [df.corr()] 또는 [np.corrcoef()]를 사용하여 구할 수 있습니다.