선형결합 / 생성 / 기저 벡터

선형결합, 생성, 기저벡터

💡 **“수학은 천재가 아닌, 적은 양의 상상의 자유를 필요로 한다. 덧붙여, 더 많은 양에서의 그것을 우린 광기라 부른다” - 수학자 앵거스 K. 로저스**

선형결합

두 벡터를 스케일하고 더하여 새 벡터를 얻는 모든 연산을 저 두벡터의 선형결합이라고 부릅니다.

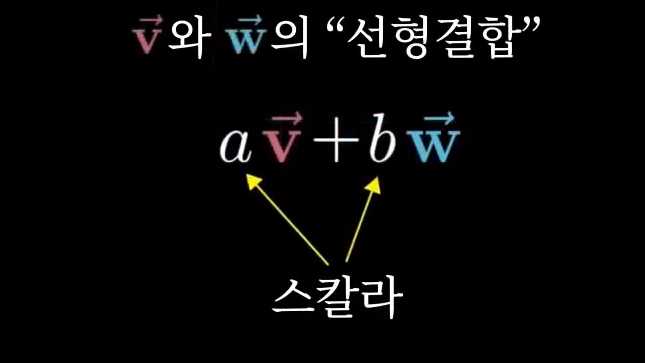
• 각 좌푯값을 스칼라로써 생각해보시기 바랍니다. 그러니까, 각 좌표값이 벡터들을 어떻게 늘이고 줄일까를 생각해보는 겁니다.
• xy 좌표게에는 특수한 벡터 두 개가 있습니다. 하나는 오른쪽을 가리키는 길이 1의 벡터이고, 흔히 i햇,이나 x-단위 벡터라 부릅니다. 다른 하나는 위쪽을 가리키는 길이 1의 벡터로, 흔히 ‘j햇’ 이나 y-단위 벡터라 부릅니다.
• 이제 우리 벡터의 x좌표를 i햇을 스케일하는 스칼라로, 즉 i햇이 숫자 3만큼 늘어난다고 생각해보고, y좌표를 j햇을 스케일하는 스칼라로, j햇이 뒤집힌 후에 숫자 2만큼 늘어난다고 생각해보죠.
• 이런 의미에서, 이 좌표쌍이 나타내는 벡터는 두 스케일된 벡터의 합입니다.
• 이것은 놀라울 만큼 중요한 개념입니다. 벡터를 ‘스케일된 두 벡터의 합’으로 보는 발상 말이죠
• 여기서 단위 백터 i햇과 j햇 둘은 특별한 이름을가지는데, 저 두 벡터를 통들어 좌표계의 기저라고 부릅니다.
• 기본적으로 기저가 의미하는 것은 이 좌표쌍을 스칼라로써 생각할 때, 그 스칼라들이 스케일하느 실제 대상들이 기저 벡터입니다.

선형 생성

• 이제 두 스칼라의 범위를 자유롭도록 놓고 여러분이 얻을 수 있는 모든 가능한 벡터를 고려해본다면 두가지 상황이 벌어지게 되는데요, 대부분의 벡터 쌍의 경우, 여러분은 평면 위 모든 점에 다다를 수 있을 겁니다. 모든 가능한 2차원 벡터가 여러분 손에 있죠.
• 하지만 두 기저 벡터가 불행히도 같은 직선상에 위치한 경우에는 결과 벡터의 끝점이 원점을 지나는 한 직선으로 제한되어버립니다.
• 사실, 정확히는 세번째 가능성도 존재합니다. 두 베터가 모두 영벡터의 경우, 그 때에는 원점에 갇혀 있게 되겠죠
• 주어진 벡터 쌍의 선형결합으로 다다를 수 있는 모든 결과 벡터의 집합을 두 벡터의 생성(선형생성)이라고합니다.

두 벡터의 선형생성의 근본적인 질문 : “벡터의 덧셈과 스칼라배, 이 두 기초 연산만 가지고 다다를 수 있는 모든 가능한 벡터들엔 무엇이 있는가?”

• 벡터의 모음을 다룰 때는, 각자를 공간상 점으로 나타내는 것이 일반적입니다.
• 점의 위치는 벡터의 끝점으로 놓고 그 벡터의 시작점(꼬리)은 보통처럼 원점에 위치한다고 생각하는 것이죠.
• 이렇게 하면, 여러분이 어떤 한 직선에 나열된 모든 가능한 벡터를 다진 그 직선 자체로 생각할 수 있게 됩니다.
  • 선은 점들의 집합이므로 모든 결과 벡터의 집합이 직선으로 표현되는 것
• 마찬가지로, 모든 가능한 2차원 벡터를 한 번에 생각할 때는 각자의 끝점이 위치하는 곳에 점으로써 개념화하게 되겠죠
• 그래서 사실상 여러분이 생각하게 될 것은 화살표가 아닌 무한한, 평평한 2차원 평면 그 자체입니다.
• 일반적으로는 벡터 자체를 생각하는 경우 화살표로 생각하고, 벡터의 모음(집합)으로 다루는 경우 점으로 생각하는 것이 편리합니다.
• 이제 선형생성으로 예시를 들자면, 대부분의 벡터의 쌍은 결국 무한한 2차원 평명 전체를 생성하기에 이릅니다. 하지만 둘이 일직선 위에 있다면, 그들의 생성은 단지 직선이죠

기저벡터

• 3차원 공간에서 서로 다른 방향을 가리키고 있는 두 벡터에 대하여 그 둘을 생성한다는 것은 무슨 의미일까요?
• 일단, 그들의 생성은 저 두 벡터의 모든 선형결합의 집합이죠. 즉, 두 벡터 각자를 스케일하여 더했을 때 얻을 수 있는 모든 가능한 벡터의 집합니다.
• 여러분은 두 벡터를 이리저리 만지며 선형결합을 정의 하는 두 스칼라를 조정하고, 그렇게 스케일된 벡터들을 더해서 만들어지는 벡터의 끝점을 따라가는 것을 상상합니다.
• 그 끝점을 3차원 공간의 원점을 지나는 어떠한 평면을 그려낼 겁니다. 이 평면이 바로 두 벡터의 생성입니다. 더욱 구체적으로 말한다면 끝점이 저 평면 위에 위치하는 모든 가능한 벡터들의 집합이 바로 두 벡터의 선형생성입니다.
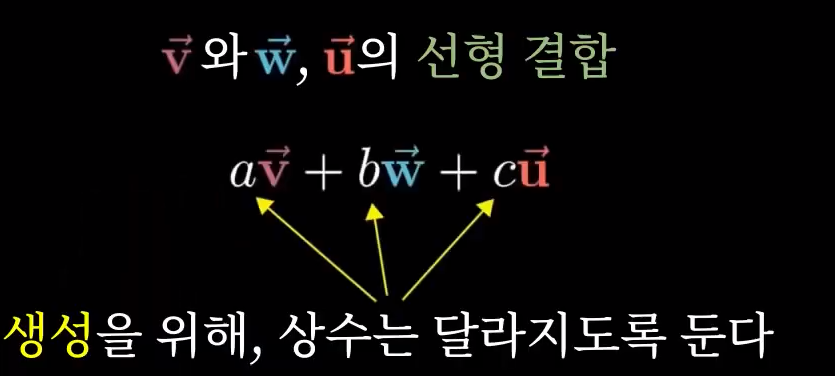
• 그럼 여기서 세 번째 벡터를 추가해 이 세 벡터의 생성을 생각한다면 무슨일이 벌어질까요?
• 세 벡터의 선형결합은 두 벡터의 선형결합과 거의 같은 방식으로 정의됩니다.
• 세 다른 스칼라를 선택하여 각 벡터를 스케일한 뒤, 모두 더하는 것이죠. 그리고 다시, 이 벡터들의 생성은 모든 가능한 선형결합의 집합입니다.
• 두 다른 경우가 벌어질 수 있습니다.
• 만약 세 번째 벡터가 다른 두 백터의 선형생성에 놓여있다면, 생성은 변화하지 않습니다. 똑같은 평면에 갇혀있게 되죠. 다른 말로, 저 선형결합에 스케일된 세 번째 벡터를 더한다고 해서 원래 생성의 바깥에 있는 새로운 벡터를 만들 수 없는 것입니다.
• 그러나 만일 세 번째 벡터를 무작위로 선정해서 두 벡터의 생성 위에 놓여 있지 않은 경우가 된다면 그것이 별개의 방향을 가리키기 때문에 모든 가능한 3차원 벡터에 접근할 수 있습니다.
• 이를 생각하고자 하는 한 방법은 여러분이 새로운 세 번째 벡터를 스케일하면 두 벡터의 생성은 평면이 그 벡터를 따라 움직이며 공간 전체를 휩쓴다는 것입니다.
• 생각해보는 또다른 방법은 여러분이 자유롭게 변화하는 세 개의 스칼라를 최대한 조정하여 3차원 공간에 접근이 가능한지 판단해 보는 것입니다.

선형 종속, 선형 독립

• 이제 이 세 번째 벡터가 다른 두 벡터의 생성에 놓이는 경우나 두 2차원 벡터가 일직선 위에 정렬한 경우처럼, 이 벡터들 중 최소한 하나는 불필요한 경우, 생성에 아무것도 더하지 못하는 경우를 설명할 어떤 용어를 원합니다.
• 이와 같은 때처럼 벡터들 중 생성의 축소 없이 하나를 제거해도 되는 경우 이와 관련된 용어로 우리는 그들이 선형종속이다라고 말합니다. 이를 다르게 말하면, 벡터 중 하나가 다른 벡터들의 선형결합으로 표현될 수있다고 말할 수 있겠죠
• 반면, 만약 벡터 모두가 각자 생성에 다른 차원을 구성한다면 그들이 선형독립이다라고 말합니다.

기저의 구체적 정의

벡터 공간의 기저는 공간 전체를 생성하는 선형 독립인 벡터의 집합