서포트 벡터 머신 (Supoort Vector Machine)

범주형 데이터나 수치(회귀)형 데이터에 모두 사용 가능한 모델
기본적으로 분류 모델을 기준으로 설명한다.

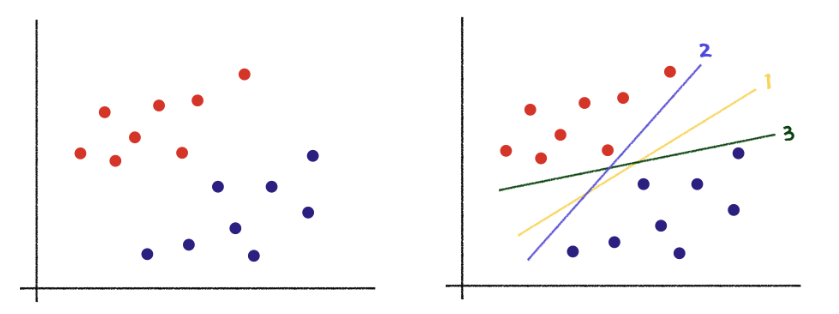
서포트 벡터 머신은 그래프의 데이터를 설명하기 위해 1, 2, 3번의 직선 모드 사용 할 수있다. 그렇지만 직관적으로 봤을 때 1번 직선이 가장 최적의 직선이라고 할 수 있다.
다음은 최적의 직선을 찾기위한 주요 용어와 지표에 대한 설명이다.

서포트 벡터 머신을 설명하는 지표, 용어

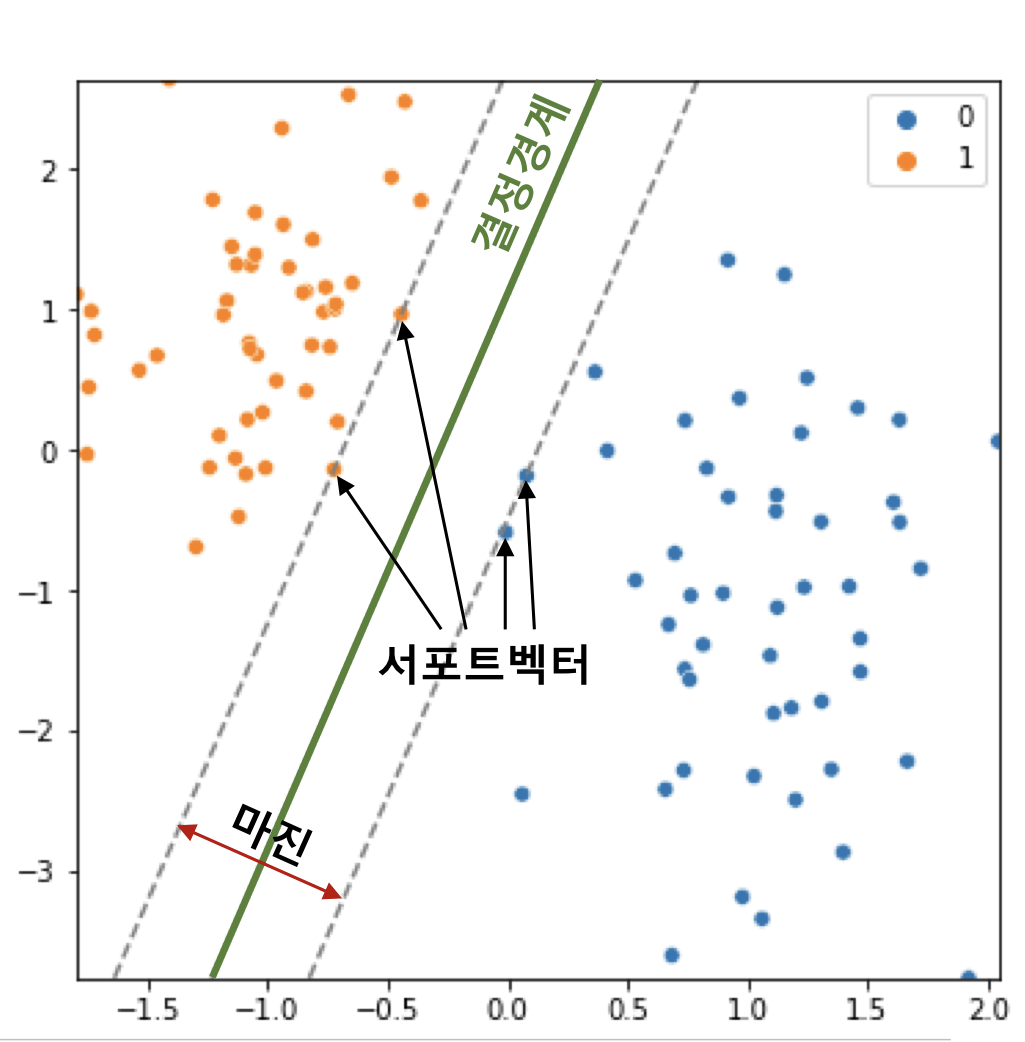
결정 경계(Decision Boundary)

• 클래스를 구분하는 경계선
• 초평면(Hyper plane)이라고 부름.
• 서포트 벡터 머신은 데이터의 스케일링에 따라 결정 경계(선, 초평면)이 달라지기 때문에 스케일링을 잘 해주는 것이 중요하다.

참고

KNN 모델
어떤 스케일러를 쓸 것인가

벡터(Vector)와 서포트 벡터(Support Vector)

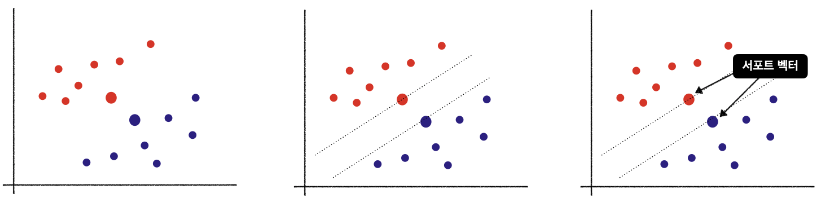
• 벡터 : 모든 데이터 포인트
• 서포트 벡터
  • 결정 경계와 가까운 데이터 포인트
  • 마진의 크기와 결졍 경계를 만들 때 기준이 되는 벡터이기 때문에 서포트 벡터라고 한다.

마진(Margin)

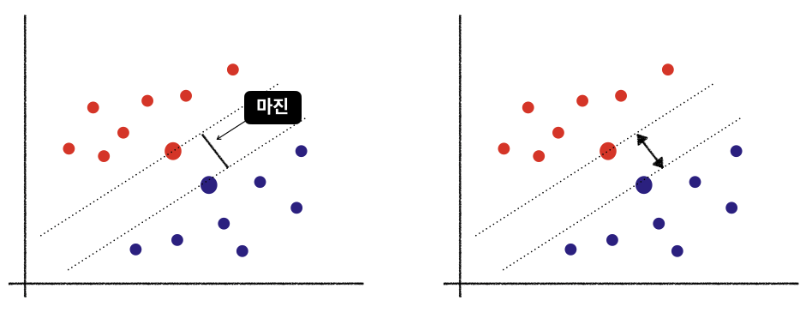
• 서포트 벡터와 결정경계 사이의 거리
• 두 집단 사이의 거리라고 표현할 수 있다.
• 마진이 클 수록 두 집단이 안정적인 분류가 가능하다.
• 마진이 크면 집단 간의 유사도가 작고(=안정적으로 잘 분류되었다.) 마진이 작으면 집단의 경계에 있는 서포트 벡터의 유사도가 높아진다.

커널 트릭(Kernel Trick)

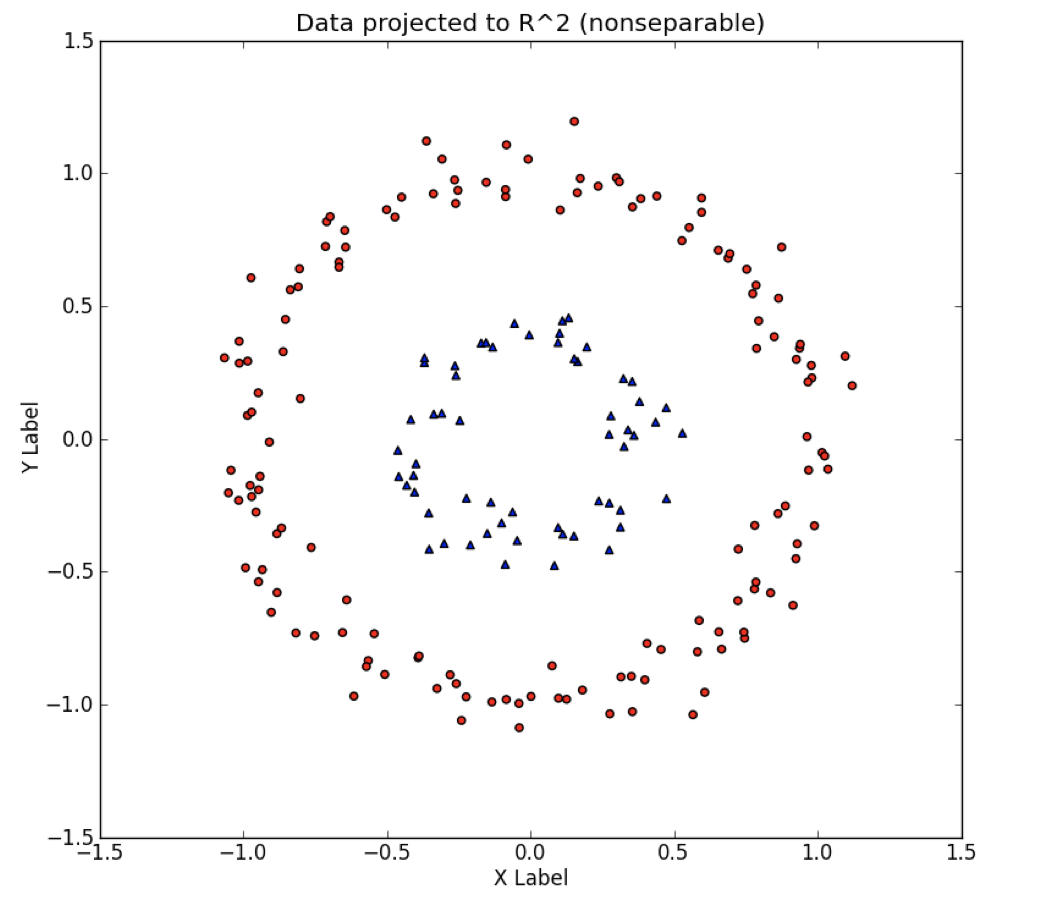
예를 들어 2차원 좌표평면 상에 존재하는 복잡한 데이터는 단순한 직선으로 분리할 수 없다.

이런 2차원 평면에 존재하는 비선형 데이터 문제를 3차원으로 변환 시키면 쉽게 집단을 분리 할 수 있다.
이렇게 저차원에서 해결하기 어려운 문제를 고차원으로 변환시켜 문제를 해결하는 것을 커널 트릭이라고 한다.

이처럼 커널 트릭을 통해 고차원에서 집단을 분리한 후 저차원으로 돌아가면 집단이 잘 분리되어있음을 볼 수 있다.

커널 종류 (sklearn.svm. 기준)

• linear : 커널트릭을 적용하지 않은 단순 벡터머신
• poly
  • Polynomial
  • degree(차수) coef0(다차향 영향도 조절, C(오차비용, 마진), gamma(결정경계 복잡도) 변수 사용
• rbf
  • Radial Basis Function
  • 가우시안 커널, 가우시안 분포(정규분포) 이용
  • C (오차 비용, 마진) gamma (결정경계 복잡도) 변수 사용
• sigmoid

Scikit Learn 패키지

from sklearn.svm import SVC, SVR

# SVC 모델의 기본 값
svc_model = SVC(C=1.0, 
			kernel='rbf', 
            degree=3, 
			gamma='scale', 
            coef0=0.0, 
            shrinking=True, 
            probability=False, 
            tol=0.001, cache_size=200, 
            class_weight=None, 
            verbose=False, 
            max_iter=-1, 
            decision_function_shape='ovr', 
            break_ties=False, 
            random_state=None)
            
svr_model = SVR(kernel='rbf', 
				degree=3, 
                gamma='scale', 
                coef0=0.0, 
                tol=0.001, 
                C=1.0, 
                epsilon=0.1, 
                shrinking=True, 
                cache_size=200, 
                verbose=False, 
                max_iter=-1)

오차 비용(C, Cost)

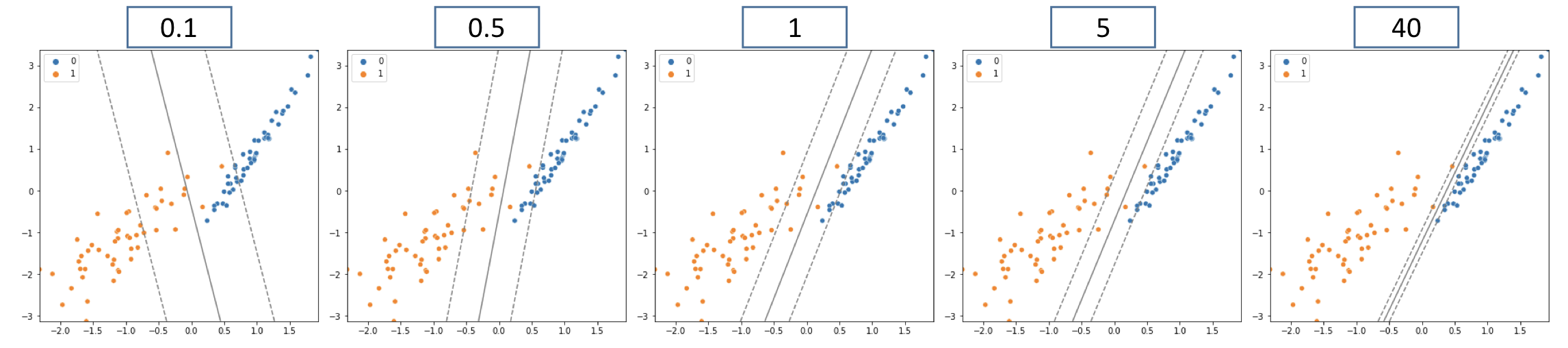
C값을 높이면

• 마진을 줄임, 오류를 허용하지 않음
• 과대적합(Overfitting) 가능성 높아짐

C값을 낮추면

• 마진이 늘어남, 오류의 허용 정도를 높임
• 과소적합(Underfitting) 가능성 높아짐

경계결정 복잡도(Gamma)

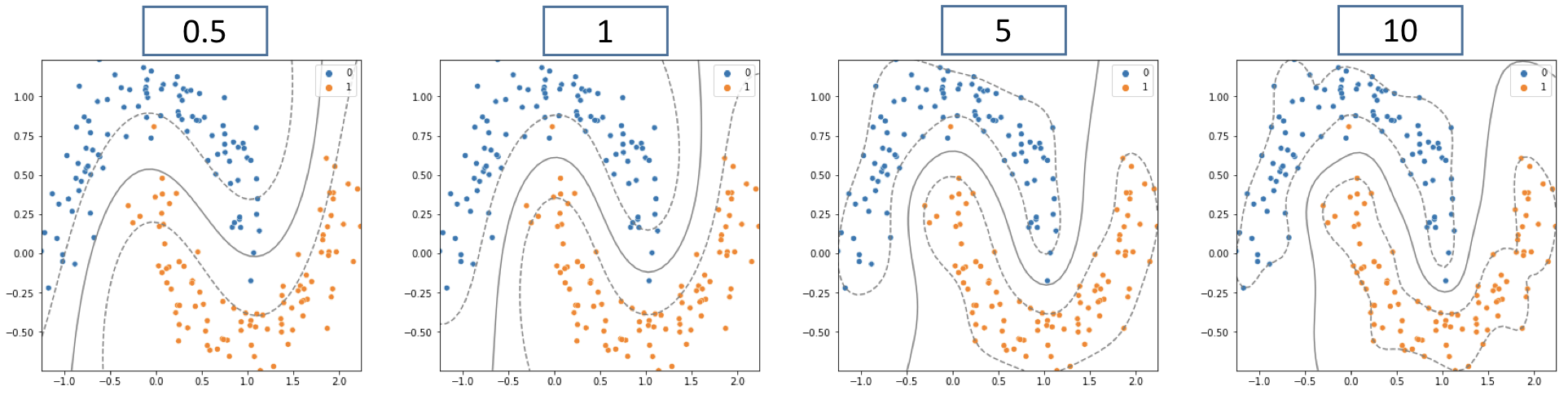
• 곡률의 크기를 결정하는 변수
• 감마 값이 커질수록 학습 데이터에 있는 모든 변수를 집단에 넣으려고함.
• KNN 모델의 K값과 비슷 (값이 커지면 모델이 복잡해짐)

Gamma값을 높이면

• 곡률(반경)이 작아짐, 모든 학습데이터에 맞춰 모델을 학습함
• 과대적합(Overfitting) 가능성 높아짐

Gamma값을 낮추면

• 곡률(반경)이 커짐, 집단을 러프하게 잡음
• 과소적합(Underfitting) 가능성 높아짐